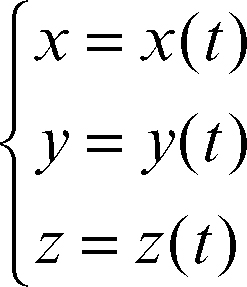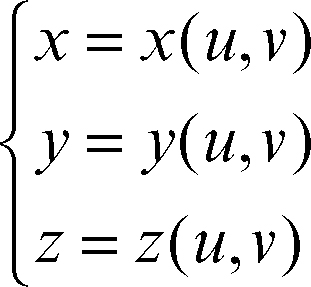parametro

parametro

parametro termine usato in particolari contesti (come per esempio quello dei polinomi o delle equazioni) per indicare una variabile indipendente, un coefficiente o una costante suscettibili di variazione all’interno di un insieme prestabilito (tipicamente reale o complesso, o più in generale in un anello). Per esempio, se è data un’equazione contenente uno o più parametri, la loro variazione permette di considerare una famiglia di equazioni, indicizzate dal parametro stesso. I parametri non vanno confusi con le incognite di un problema e, per distinguere un parametro da un’incognita, è necessario che queste ultime siano specificate come un dato del problema. Solitamente (ma non di regola) le ultime lettere dell’alfabeto x, y, z sono riservate alle incognite o alle variabili. Data per esempio l’equazione generale della retta nel piano y = mx + q, le variabili dell’equazione sono x e y e variano nell’insieme R dei numeri reali; m e q indicano invece due parametri, anch’essi variabili nell’insieme dei numeri reali. Al variare di tali parametri si ottengono tutte le rette del piano non parallele all’asse delle ordinate: essi rappresentano rispettivamente l’inclinazione della retta (il coefficiente angolare m) e l’ordinata della sua intersezione con l’asse delle ordinate (il termine noto q). Similmente, nell’equazione generale della circonferenza (x − x₀)² + (y − y₀)² = r ², le variabili incognite sono x e y mentre x₀, y₀ e r sono tre parametri che rappresentano rispettivamente l’ascissa del centro della circonferenza, l’ordinata del centro della circonferenza e il raggio della circonferenza: al variare di tali parametri in R si descrivono tutte le circonferenze del piano.

Nella discussione di un problema, si parla di problema con parametro quando un dato del problema è supposto noto, ma non è numericamente specificato. Ciò permette al problema particolare di acquisire maggiore generalità: un problema con parametro rappresenta, al variare del parametro, una classe infinita di problemi, indicizzati dal parametro stesso. Un parametro che non è fatto variare all’interno del problema è detto parametro costante ed è trattato in tutto e per tutto come un effettivo dato numerico. Il parametro diventa invece un parametro variabile nel momento in cui si discute il problema, vale a dire quando si analizzano le diverse soluzioni del problema al variare del parametro stesso, stabilendo per quali valori di esso la soluzione è univocamente determinata o se invece il problema ha tante, infinite o nessuna soluzione (→ problema, discussione di un).

Formule ed equazioni parametriche

Una curva o una superficie possono essere espresse analiticamente utilizzando uno o più parametri che descrivono la variabilità di alcune sue caratteristiche. L’oggetto geometrico risulta descritto da una o più funzioni la cui espressione contiene i parametri introdotti, che variano all’interno di un determinato intervallo. Per esempio, una conica può essere espressa in forma polare dall’equazione

dove e è la sua eccentricità, k rappresenta la metà della lunghezza della corda condotta per il fuoco normalmente all’asse focale e θ è variabile indipendente. Il valore di ρ, per una conica, fissate e e k, dipende quindi dal valore del parametro θ: fissato un valore di θ all’interno dell’opportuno intervallo di variazione, si individua il punto di coordinate polari (ρ, θ) appartenente alla conica.

Nello spazio, le equazioni parametriche di una curva in coordinate cartesiane, sono del tipo

dove t è il parametro. Le equazioni parametriche di una superficie dipendono invece da due parametri e sono del tipo: