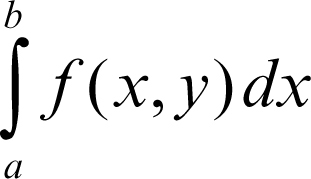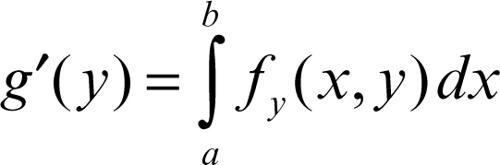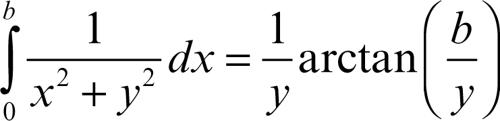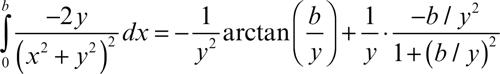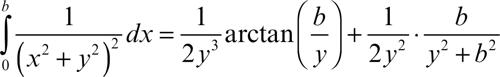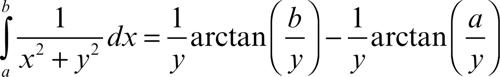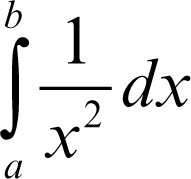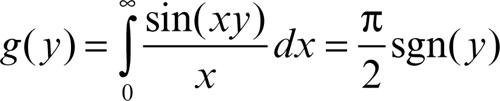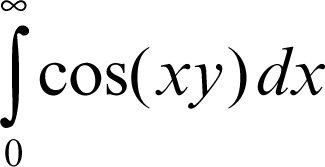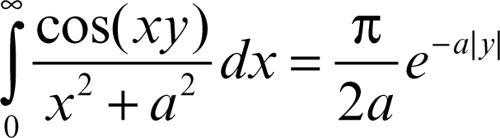limite, passaggio al
limite, passaggio al
limite, passaggio al (sotto il segno di integrale) i teoremi di passaggio al limite e di derivazione sotto il segno di integrale forniscono delle condizioni sufficienti affinché in un integrale definito dipendente da un parametro sia possibile scambiare le operazioni di integrale e di limite o di derivata rispetto al parametro.
Sia ƒ(x, y) una funzione continua nel rettangolo R = [a, b] × [α, β] e la si pensi come funzione di x con parametro y. Allora l’integrale
è una funzione g(y) continua in [α, β]. Se poi anche la derivata parziale ƒy(x, y) è continua, g(y) è derivabile e risulta
Per esempio, l’integrale
è continuo per y variabile in ogni intervallo che non contenga l’origine. Derivando rispetto a y si ha
da cui
Invece, se 0 < a < b, l’integrale
è continuo anche per y = 0 risultando il suo limite
che è il valore di
Il risultato non si estende a un integrale improprio, per esempio, su un intervallo illimitato. Come esemplificazione di questo fatto si consideri la funzione
Essa non è continua per y = 0, dove ha un salto (la funzione integranda sulla retta x = 0 ha una discontinuità, ma eliminabile ponendo ƒ(0, y) = y); la derivata per y ≠ 0 è nulla, ma l’integrale
non converge. Per poter trattare questi casi è necessario avvalersi di teoremi sull’integrale di → Lebesgue, in particolare quello della convergenza dominata. Per esempio, l’integrale
è continuo rispetto a y perché la funzione integranda ammette la maggiorante integrabile
ma non è derivabile perché la derivata parziale
non è assolutamente integrabile sull’intervallo illimitato [0, +∞).