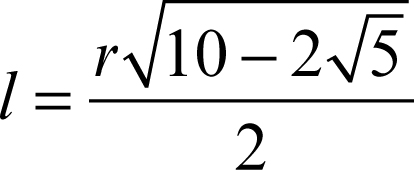pentagono

pentagono

pentagono poligono con cinque lati e cinque angoli. Ha cinque diagonali e la somma dei suoi angoli interni è pari a 540°. Se i lati e gli angoli hanno tutti uguali misure è detto pentagono regolare. Un pentagono regolare è inscrivibile e circoscrivibile a una circonferenza, ha per assi di simmetria gli assi dei suoi lati, ma non è simmetrico centralmente. Ciascuno degli angoli di un pentagono regolare misura 3π/5, cioè 108°, e un pentagono regolare di lato l ha apotema

e area

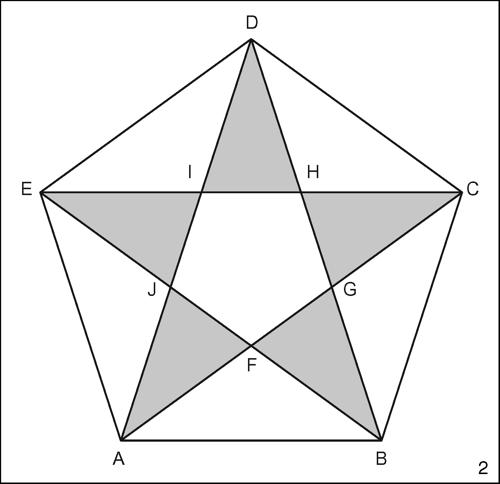
Tracciando le diagonali (o prolungando i lati) di un pentagono si ottiene un pentagramma o stella a cinque punte. Il pentagono viene scomposto in un pentagono simile e in dieci triangoli. I triangoli appartengono a due tipologie particolari: 1) triangoli isosceli con angolo al vertice (36°) pari a metà dell’angolo alla base (72°); 2) triangoli isosceli con angolo alla base (36°) pari a un terzo dell’angolo al vertice (108°). La particolarità di tali triangoli è che il rapporto tra il lato maggiore e quello minore è uguale al → numero aureo. Da ciò segue che il rapporto tra la diagonale e il lato del pentagono regolare è uguale al numero aureo

Il lato l del pentagono inscritto in una circonferenza di raggio r si ottiene dalla relazione

e risulta uguale all’ipotenusa di un triangolo rettangolo che ha per cateti il raggio r e la parte aurea di r.

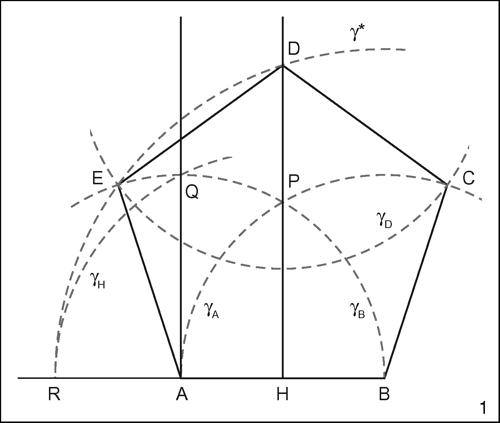
Il pentagono regolare è costruibile con riga e compasso, sia assegnandone il lato, sia assegnando una circonferenza in cui si considera inscritto. Assegnato il lato AB, si indica con P uno dei due punti d’intersezione delle circonferenze γ_B e γ_A, di rispettivi centri A e B e di raggio AB, e da P si traccia la perpendicolare PH ad AB. Si determina poi il punto Q, intersezione tra γ_B e la perpendicolare per A ad AB. Con centro in H si traccia la circonferenza γ_H di raggio HQ, che interseca in R il prolungamento del segmento AB, dalla parte di A. Con centro in B e raggio BR si traccia ora la circonferenza γ* e si considerano le sue intersezioni D, E rispettivamente con la retta PH e con la circonferenza γ_B. Infine si determina il punto C intersecando la circonferenza γ_A con la circonferenza γ_D di centro D e raggio della stessa lunghezza di AB. Il poligono ABCDE è il pentagono regolare costruito su AB.