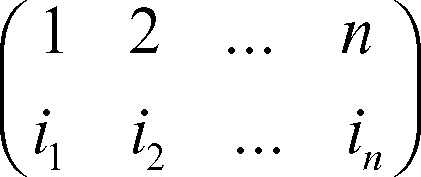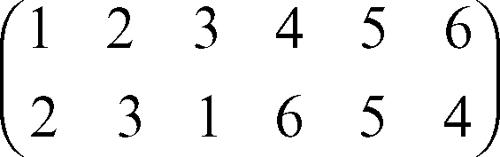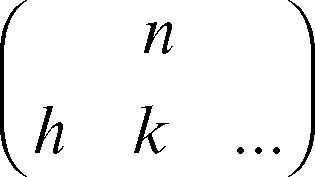permutazione

permutazione

permutazione nel calcolo combinatorio, biiezione di un insieme A, finito, su sé stesso. Indicando gli elementi di A con 1, 2, …, n, una permutazione si può rappresentare con lo schema

essendo i_j il corrispondente del generico elemento j. Per estensione di significato, è detto permutazione anche ognuno degli ordinamenti i₁, …, i_n così ottenuti. In altri termini, si dice permutazione semplice di n elementi ognuna delle sequenze ordinate che si può costituire disponendo in un dato ordine gli n elementi. Il numero di tutte le possibili permutazioni di A è indicato con P_n ed è dato da n! = 1 ⋅ 2 ⋅… ⋅ n (il simbolo n! si legge «n fattoriale»). Poiché le permutazioni sono biiezioni di un insieme finito in sé, tra permutazioni è definita l’operazione di composizione. L’insieme delle permutazioni su n elementi dotato di tale operazione di composizione forma un gruppo, detto → gruppo simmetrico e indicato con S_n. Particolari permutazioni sono il ciclo, che fa corrispondere a ogni elemento di un elenco ordinato il successivo e all’ultimo il primo, e la trasposizione, che è un ciclo di ordine 2, cioè scambia tra loro due elementi di A lasciando gli altri invariati. Ogni permutazione può essere scritta come prodotto di cicli disgiunti (cioè non aventi alcun elemento uguale).

Per esempio, la permutazione

può essere scritta come (1, 2, 3)(4, 6). A sua volta, ogni ciclo può essere scritto come prodotto di trasposizioni (ma non più necessariamente disgiunte). Per esempio, (1, 2, 3) = (1, 2) (1, 3). Ne segue che ogni permutazione di n numeri successivi (da 1 a n) si può ottenere dalla permutazione con gli n numeri in ordine crescente componendo un numero finito di trasposizioni: a seconda che il numero di tali trasposizioni sia pari oppure dispari, la permutazione si dice di classe pari oppure di classe dispari. La precedente permutazione è, per esempio, di classe dispari perché risulta composta dalle tre trasposizioni (1, 2)(1, 3)(4, 6). Il sottoinsieme A_n delle permutazioni di classe pari di S_n è detto → gruppo alterno; è un sottogruppo normale di S_n e, per n > 4, è un gruppo semplice, privo cioè di sottogruppi normali non banali.

Quando si vuole conoscere il numero delle permutazioni di n oggetti alcuni dei quali sono uguali tra loro si parla di permutazione con ripetizione e si ha:

in cui alcuni oggetti sono ripetuti h volte, altri k volte ecc. Tale numero è anche indicato con

ed è detto coefficiente multinomiale. Nel caso di disposizione circolare di n elementi, come per esempio n oggetti disposti attorno a un tavolo circolare, allora il numero delle permutazioni, in questo caso dette permutazioni circolari, è:

È infine detta matrice permutativa o matrice di permutazione una matrice quadrata ottenuta dalla matrice identità mediante una permutazione delle sue righe.