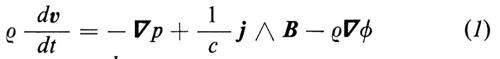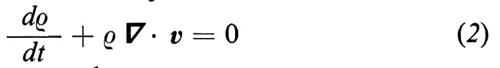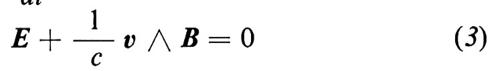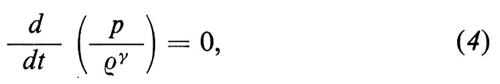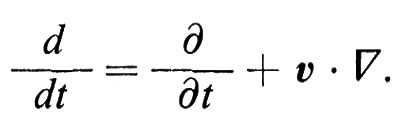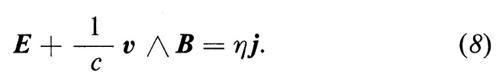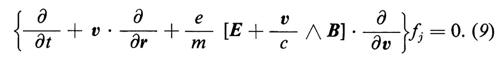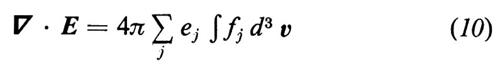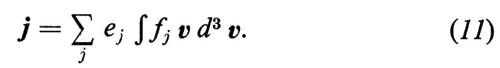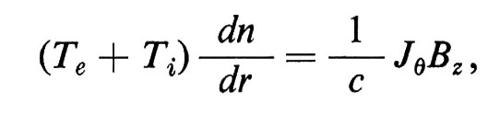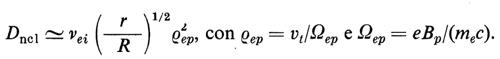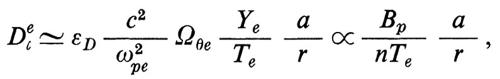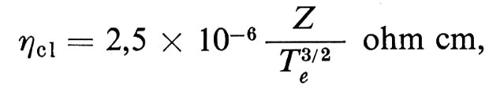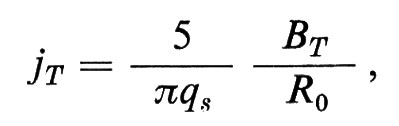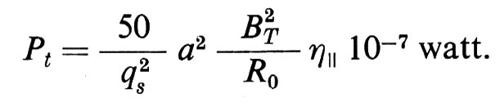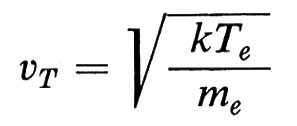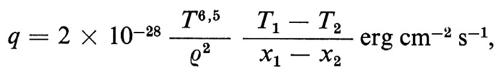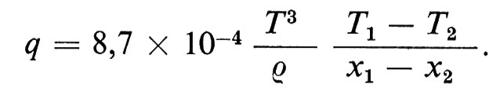Plasmi

Plasmi

di Bruno Coppi, Yaguri B. Zeldovich

PLASMI

Plasmi in fisica di Bruno Coppi

sommario: 1. Introduzione. 2. Descrizione teorica. a) Approssimazione magnetoidrodinamica ideale. b) L'equazione di Vlasov. 3. Importanza delle instabilità in un plasma. 4. Interazioni tra onde e particelle e smorzamento di Landau. 5. Configurazioni toroidali: confinamento a corrente diffusa. 6. Diffusione ‛classica', ‛neoclassica' e ‛anomala'. 7. Il problema del riscaldamento. 8. Esperimenti toroidali a corrente diffusa. 9. La configurazione stellarator. 10. Multipoli toroidali. 11. La prossima generazione di esperimenti con plasmi termonucleari. 12. Geometrie a estremi aperti: specchi magnetici. 13. Sistemi lineari e toroidali con β finito. 14. Fusione a confinamento inerziale. 15. Esperimenti di base nella fisica dei plasmi. 16. Realizzabilità scientifica della fusione termonucleare controllata. □ Bibliografia.

1. Introduzione

Lo studio dei gas ionizzati è tra i più antichi e più fruttuosi campi della fisica. A questo proposito basta ricordare che la fisica molecolare, la fisica atomica e la fisica nucleare sono nate essenzialmente dallo studio della conduzione elettronica nei gas. La ricchezza dei fenomeni scoperti in ognuno di questi campi fu tale da distogliere l'interesse dallo studio dei fenomeni collettivi presenti nelle scariche elettriche. Un più valido impulso allo studio dei plasmi (v. Langmuir, 1939) venne dato dagli astrofisici (v. Alfvén, 1950), interessati ai vari processi di emissione di radiazione dal Sole e dalle stelle oltre che allo studio dello spazio interplanetario e interstellare, e dai geofisici, interessati. alla dinamica della ionosfera (v. Cowling, 1957). In seguito, lo sviluppo delle armi termonucleari e l'inizio degli studi sulla possibilità di realizzare un reattore per la produzione di energia basato su reazioni di fusione nucleare (v. cap. 16) diedero il maggiore impulso all'acquisizione di un complesso organico di conoscenze sperimentali e teoriche sulla dinamica dei plasmi. Tale insieme di conoscenze si è rivelato, a sua volta, di grande importanza nei più recenti sviluppi della fisica dello spazio (per es. nell'esplorazione della magnetosfera terrestre) e per comprendere la natura dei nuovi oggetti (come le stelle a raggi X e le pulsar) scoperti in questi ultimi anni.

Con il termine ‛plasma' si intende generalmente un sistema di particelle caratterizzato da forze di interazione a lungo raggio (di tipo coulombiano o gravitazionale), con densità sufficientemente bassa perché la forza agente su una qualunque particella, dovuta alle particelle più vicine, sia molto minore di quella esercitata dal complesso delle particelle più distanti. Per esempio, nel caso di un plasma composto di elettroni e nuclei, che sia nel complesso elettricamente neutro, le interazioni elementari tra le particelle che lo compongono sono ben conosciute e sono descritte dalla forza di Lorentz. I campi che generano tali forze si calcolano mediante le equazioni di Maxwell a partire dalle densità di carica e di corrente dovute alla posizione e alla velocità delle particelle.

La nostra attenzione sarà principalmente rivolta a plasmi con temperature elevate del tipo di quelli che interessano la fusione termonucleare controllata (v. cap. 16). In questo caso gli effetti quantistici non sono rilevanti, nel senso che i livelli energetici che un plasma eccitato può raggiungere corrispondono a un gran numero di quanti di energia. In particolare, per un plasma immerso in un forte campo magnetico, la frequenza di ciclotrone Ω_e = eB/mc e quella di Langmuir ω_pe = (4ππe²/m)^1/2 sono le frequenze caratteristiche più elevate proprie della dinamica degli elettroni ed è facile vedere che nei regimi di plasma che maggiormente ci interessano l'energia termica degli elettroni kT_e è molto maggiore sia di ℏω_pe sia di ℏΩ₂; inoltre, come già accennato, le forze tra le particelle sono deboli, in quanto e²n^-1/3 ≪ kT_e (e indica la carica degli elettroni, m la loro massa, ℏ la costante di Planck divisa per 2π n la densità delle particelle, B il campo magnetico, c la velocità della luce, k la costante di Boltzmann e T_e la temperatura degli elettroni).

Nonostante queste caratteristiche apparentemente semplici, solo in parte si è riusciti a comprendere la dinamica dei plasmi e solo di recente le sue più rilevanti formulazioni teoriche hanno cominciato a trovare conferma sperimentale. E ciò per diverse ragioni. Una di esse è che le interazioni elettromagnetiche sono caratterizzate da forze a lungo raggio, perciò le proprietà dei plasmi rarefatti ad alta temperatura non sono di carattere locale e la geometria delle varie configurazioni possibili ha su di esse notevole influenza. Un'altra ragione deriva dal fatto che le equazioni che descrivono la dinamica dei plasmi non sono lineari, per cui non è possibile, contrariamente a quanto avviene in molti altri casi, considerare un plasma come un sistema semplice in cui la risposta a una data sollecitazione è proporzionale al fattore che rappresenta tale sollecitazione.

In particolare ricordiamo che un plasma del tipo realizzato per reattori termonucleari non può, in generale, essere descritto come un fluido ordinario in termini di densità, pressione e velocità (macroscopica) di flusso: bisogna piuttosto ricorrere all'uso della funzione di distribuzione f(r, v, t) delle particelle nello spazio delle fasi. Ricordiamo che, se con r si indica la coordinata spaziale della particella, con v la sua velocità e con I il tempo, l'espressione f(r, v, t) dr dv rappresenta il numero di particelle contenute al tempo t nel volume elementare dr intorno al punto e e con velocità comprese in un intervallo dv intorno a v. Nella teoria dei plasmi si ha quindi a che fare con equazioni molto più complesse rispetto a quelle usàte nella normale fluidodinamica. Infatti la funzione f dipende da 7 variabili indipendenti, mentre nel caso in cui si possa adottare una descrizione di tipo fluido si ha a che fare con funzioni di 4 variabili soltanto: r e t.

2. Descrizione teorica

a) Approssimazione magnetoidrodinamica ideale

Per la descrizione teorica di un plasma viene usato il seguente sistema di equazioni:

che descrive macroscopicamente la dinamica del plasma, combinato con le equazioni di Maxwell:

Facciamo osservare che queste equazioni descrivono in modo appropriato un fluido con conducibilità elettrica infinita e conducibilità termica nulla, che soddisfi l'equazione di stato adiabatica (4); in esse ρ e è la densità di massa, v la velocità del fluido, p la pressione, ϕ il potenziale prodotto da una forza esterna, per esempio gravitazionale, j la densità di corrente, B l'induzione magnetica ed E il campo elettrico. È stato adottato il sistema di unità di Gauss e si è indicata la derivata lagrangiana (totale) con il simbolo

Affinché la trattazione fluidodinamica sia teoricamente valida, è necessario che il cammino libero medio delle particelle sia molto più piccolo di tutte le lunghezze che caratterizzano il particolare problema per il quale si sono scritte le equazioni (1)-(7). In particolare, una delle più drastiche limitazioni per l'approssimazione magnetoidrodinamica ideale è data dall'equazione (3), che lega il moto del fluido a quello delle linee di forza del campo magnetico. Un caso in cui tale vincolo non viene rispettato si ha quando si deve tener conto della resistività elettrica del plasma, indicata nel seguito con η, per cui, al posto dell'equazione (3), bisogna scrivere

Il ruolo della resistività appare quindi evidente in quegli aspetti della dinamica dei plasmi che interessano moti di particelle disaccoppiati da quelli del campo magnetico. Un caso tipico in cui interessa considerare il moto del plasma disaccoppiato da quello del campo magnetico si ha nelle configurazioni di campo contenenti ‛linee neutre', lungo le quali il valore del campo è nullo. Configurazioni di questo tipo sono considerate frequentemente in astrofisica per modelli teorici (v. Petschek, 1963) atti a descrivere processi in cui avviene una trasformazione di energia magnetica in energia cinetica (v. fig. 1). È evidente che per descrivere la regione intorno al punto O, in cui sia v che B sono nulli, non si può trascurare nell'eq. (8) il termine resistivo ηj. Lo stesso si può anche dire quando vengono considerati gli effetti della componente del campo elettrico lungo la direzione del campo magnetico B. In seguito saranno menzionati alcuni altri casi significativi in cui la resistività assume, da questo punto di vista, un ruolo importante.

b) L'equazione di Vlasov

Se i problemi da trattare non permettono una descrizione fluidodinamica, in quanto tutte le scale delle distanze coinvolte sono minori del cammino libero medio di collisione tra le particelle, si fa uso di un'equazione relativamente semplice per la funzione di distribuzione f: la cosiddetta equazione di Vlasov, che è simile formalmente all'equazione di Boltzmann senza termine collisionale,

Nella (9) E e B sono i campi elettrici e magnetici autocompatibili, originati dalla carica e dalla corrente totali deducibili dalla funzione di distribuzione delle particelle stesse. In altri termini, E soddisfa l'equazione di Poisson

(l'indice j indica le varie specie di particelle) e, insieme a B, le equazioni di Maxwell per il campo elettromagnetico, nelle quali la densità di corrente è data da

Va notato che in una descrizione di questo tipo scompaiono tutte le fluttuazioni dei campi a livello microscopico che derivano dalla natura discreta delle particelle.

Una descrizione simile viene fatta quando si rappresenta una galassia come un plasma gravitazionale in cui le stelle rappresentano le componenti elementari (v. Lin, 1967). La differenza principale rispetto ai plasmi elettrodinamici usuali sta nel fatto che nel caso gravitazionale si ha un solo tipo di particelle, soggette a forze attrattive. Va anche ricordato che la descrizione mediante l'equazione di Vlasov presuppone che il numero di particelle contenute in una sfera di Debye sia grande, cioè che sia nλ3_D ≫ 1; nel caso di un plasma ordinario, λ_D = [kT/(4πn e²)]^1/2 = v_t/ω²_p√-2 è la lunghezza di Debye e v, = (2kT/me)¹¹² è la velocità termica degli elettroni. La lunghezza di Debye misura la distanza oltre la quale la carica di uno ione risulta sostanzialmente schermata.

La natura non lineare della dinamica di un plasma appare evidente dalla struttura delle equazioni idromagnetiche oltre che dalla già citata equazione di Vlasov. D'altra parte le caratteristiche non locali dei plasmi con un cammino libero medio collisionale sufficientemente grande sono indicate dalle equazioni integrali che si ricavano dalle equazioni (9), (10) e (11): esse coinvolgono contemporaneamente lo spazio delle velocità, descritto dalla variabile indipendente v, e lo spazio geometrico ‛reale' descritto da r.

Se poi interessa anche tener conto degli effetti degli urti ‛discreti' delle singole particelle, l'esatta equazione cinetica per f si ottiene aggiungendo a secondo membro dell'equazione (9) un opportuno termine (∂f/∂^t)_c, per descrivere le variazioni di f dovute a questi urti. Per ragioni di convenienza, a seconda del tipo di problema da analizzare, possono essere adottate diverse forme dell'operatore di collisione. (Per una estesa discussione ditale argomento si veda il trattato di Montgomery e Tidman, 1964).

3. Importanza delle instabilità in un plasma

Per iniziare con un esempio importante, consideriamo un plasma non omogeneo immerso in un intenso campo magnetico. Una delle configurazioni più semplici è data da un cilindro di plasma con un campo magnetico B diretto lungo l'asse. L'andamento della densità e della pressione è del tipo indicato nella fig. 2. Un plasma così confinato diffonde attraverso il campo magnetico in conseguenza degli urti individuali tra elettroni e ioni e di modi collettivi che si sogliono indicare col termine di instabilità. In altre parole, le numerose instabilità cui va soggetto un plasma in un campo magnetico possono portare a perdite di particelle e di energia attraverso il campo magnetico molto più rapidamente di quanto non derivi dagli urti individuali; questi meccanismi sono più importanti in regimi di alte temperature, in cui le frequenze di collisione divengono molto basse.

Le instabilità di un plasma vengono anche prese in considerazione per descrivere, ad esempio, l'insorgere di processi in cui l'energia si trasforma da magnetica in cinetica, o di meccanismi di accelerazione di particelle, o di uno stato di turbolenza del plasma, o di oscillazioni coerenti e così via. La denominazione di instabilità per una così larga varietà di fenomeni deriva dai procedimenti analitici che si adottano per descriverli e che seguono strettamente la descrizione analitica delle instabilità di un fluido. Infatti spesso si osserva che l'insorgere di un'instabilità in un plasma indica la transizione da uno stato O di equilibrio a uno stato I senza distruzione del sistema.

Lo stato di equilibrio si ottiene come soluzione della forma stazionaria delle equazioni usate per descrivere il plasma. Per esempio la descrizione fluida dello stato di equilibrio della configurazione indicata nella fig. 2, su intervalli di tempo più brevi del tempo di diffusione per collisioni, è data semplicemente da

dove T_i,e rappresenta la temperatura ionica o elettronica che si suppone costante, n la densità delle particelle e θ la direzione azimutale. Consideriamo ora una piccola perturbazione dello stato di equilibrio, tale che la densità totale delle particelle sia n_t = n + í, con í ≪ n, e trascuriamo nelle equazioni che descrivono il plasma tutti i termini quadratici in í e di ordine superiore in ∣ í/n ∣ . La dipendenza temporale di í è data allora da

í = ñ exp(−iωt);

se, dopo aver risolto rispetto a í le equazioni linearizzate del plasma, si trova che Im(ω) = γ > O, si è allora in presenza di un'instabilità. Questo indica evidentemente che il sistema tende ad allontanarsi dallo stato di equilibrio O, ma non dice nulla sulla natura dello stato 1. Per descrivere completamente la transizione bisognerebbe risolvere equazioni in cui i termini non lineari nella perturbazione í non vengano trascurati e ciò nella maggior parte dei casi è estremamente difficile. Ci sono tuttavia criteri per classificare le instabilità tenendo conto delle proprietà del nuovo stato 1. Una prima distinzione si può fare tra ‛macroinstabilità' e ‛microinstabilità'. Nelle prime sono coinvolti moti su larga scala che tendono a distruggere la configurazione iniziale del plasma e che, per esempio, sono descritti dall'insieme delle equazioni idromagnetiche (1)-(7). Alcune di queste instabilità sono, infatti, come vedremo, molto simili a quelle idrodinamiche che si creano allorché un fluido, di data densità, viene posto al di sopra di uno di più bassa densità in un campo gravitazionale diretto verso il basso.

Le microinstabilità si distinguono ulteriormente in instabilità cinetiche, quando occorre prendere in considerazione la funzione di distribuzione nello spazio delle velocità e quindi le relative equazioni cinetiche per questa funzione, e instabilità di tipo fluido, quando si possono descrivere mediante i momenti della funzione di distribuzione, come ad esempio la densità, la temperatura, ecc. A questa classe appartengono le instabilità dovute agli effetti di resistività del plasma. L'instabilità detta onda ionico-acustica (v. cap. 4), derivante dal formarsi di una corrente elettronica che scorre a una velocità u_e > (T_e/m_i)^1/2 in un plasma a elevata temperatura (m_i indica la massa degli ioni), va descritta invece con l'equazione di Vlasov e appartiene alla classe delle microinstabilità cinetiche.

Particolare importanza riveste il caso in cui la frequenza di oscillazione di una determinata microinstabilità è molto maggiore del suo tasso di accrescimento, cioè Re(ω) ≫ Im(ω). Instabilità di questo tipo sono anche indicate col termine di onde autoeccitate; si può descrivere l'interazione tra un'onda e un certo tipo di particelle, oppure tra onde differenti, mediante i procedimenti teorici di cui si fa normalmente uso in meccanica quantistica.

Va notato che tutte le macroinstabilità descritte dal sistema di equazioni (1)-(7) sono date da modi puramente crescenti, nel senso che appena prodotte - la loro dipendenza temporale è data da exp(−iωt). Una forma particolarmente importante di macroinstabilità è il cosiddetto ‛modo di scambio', che è molto simile alla ben nota instabilità di Rayleigh-Taylor della fluidodinamica.

Per illustrare quanto detto facciamo riferimento alla fig. 3: un bicchiere d'acqua è rovesciato (v. Chen, 1967) e all'inizio l'acqua è separata dall'aria da un pistone a tenuta senza né peso né attriti (la forza di gravità è rivolta verso il basso). In queste condizioni l'acqua è trattenuta dalla pressione dell'aria (fig. 3A). Una volta tolto il pistone, però, se si sviluppa una piccola increspatura, questa tende ad accrescersi, dato che la colonna d'acqua che preme verso il basso sulla parte convessa dell'increspatura è più alta di quella sovrastante la parte concava. Alla fine l'acqua cadrà dal bicchiere (fig. 3C).

Riferendoci ora alla fig. 4, consideriamo un plasma sostenuto contro la gravità da un campo magnetico diretto lungo l'asse z; all'inizio sul piano x = O la densità passa bruscamente a zero da un valore finito. Quindi, se si forma un increspatura, questa tende ad aumentare man mano che diminuisce l'energia potenziale gravitazionale del plasma, mentre l'energia magnetica di richiamo rimane immutata. Ciò si verifica in quanto, come segue dalla condizione E + (v ⋀ B)/c = O, il campo magnetico resta congelato nel plasma e la formazione di una increspatura provoca uno scambio e uno spostamento delle linee magnetiche, senza peraltro far variare l'energia magnetica, dato che il campo magnetico rimane costante.

Un plasma è soggetto a instabilità di scambio anche quando è contenuto in un campo magnetico non omogeneo, le cui linee di campo siano concave verso la regione di densità crescente. In questo caso la curvatura delle linee magnetiche sostituisce l'effetto del campo gravitazionale. Un'altra forma di macroinstabilità, che descriveremo nel cap. 5, è data dal ‛modo a serpentina' (o kink). Come vedremo, l'insorgere di questa instabilità dipende dalla distribuzione dei campi magnetici e delle correnti nel plasma.

Il modo di scambio dipende invece dalla densità di energia cinetica del plasma e rappresenta un'espansione del plasma attraverso il campo magnetico quando la direzione lungo la quale la pressione cinetica diminuisce coincide con una direzione lungo cui diminuisce anche la densità di energia magnetica. Ciò suggerisce che, per evitare l'insorgere di instabilità di scambio, occorra, per esempio, creare configurazioni con B minimo, ovvero una buca magnetica del tipo di quella che verrà descritta nel cap. 12.

4. Interazioni tra onde e particelle e smorzamento di Landau

Consideriamo per semplicità una funzione di distribuzione delle particelle f(v) unidimensionale, che descrive un plasma in cui sia stata eccitata un'onda con velocità di fase = w/k, dove k è il numero d'onda nella direzione di v. Le particelle con velocità compresa in un intorno di v' possono scambiare energia e quantità di moto con l'onda. Se però, come nel caso rappresentato nella fig. 5, il numero di particelle più lente dell'onda è maggiore di quello delle particelle più veloci, l'onda accelererà più particelle di quante non ne rallenti e quindi trasferirà energia alle particelle con velocità compresa in un intorno di v': come conseguenza si avrà uno smorzamento dell'onda. Landau nel 1946 previde teoricamente tale effetto per le onde di Langmuir; di qui il nome di ‛smorzamento di Landau' dato a processi di questo tipo.

Se invece la distribuzione di particelle è caratterizzata da una velocità macroscopica di flusso u, maggiore di v', come nella fig. 6, il numero delle particelle più veloci dell'onda è maggiore di quello delle particelle più lente e l'onda tende ad accrescersi: è questa l'origine della instabilità dovuta alla formazione di un'onda ionico-acustica cui si è accennato nel cap. 3.

Quando si è in presenza di un intenso campo magnetico, indicando con il simbolo la direzione a esso parallela, la condizione di risonanza tra onda e particelle diviene

ω − k_IIv_II + n⁰Ω = 0, (12)

dove n⁰ è un numero intero e Ω = eB/mc è la frequenza di ciclotrone della particella. Si può comprendere questa condizione osservando che l'energia e il momento dell'onda sono rispettivamente ℏω e ℏk. Si ha pertanto che il bilancio dei momenti nella direzione del campo magnetico è dato da

ℏk_II + mΔv_II = 0 (13)

e quello dell'energia da

ℏω + mv_IIΔv_II + ℏn⁰Ω = 0; (14)

v_IIΔv_II e ℏn⁰Ω rappresentano rispettivamente la variazione di energia delle particelle nella direzione parallela e perpendicolare al campo. Combinando la (13) e la (14) si ottiene la (12).

Va notato che la componente del momento perpendicolare al campo magnetico viene assorbita dal campo stesso.

Un caso particolarmente significativo si ha quando la frequenza dell'onda, ω, è molto più piccola della frequenza di ciclotrone. In queste condizioni non c'è quasi scambio di energia tra le particelle e l'onda, ma soltanto un cambiamento del passo dell'elica percorsa dalle particelle. Un processo di questo tipo costituisce quindi un meccanismo per trasformare l'energia acquistata dalle particelle nella direzione del campo magnetico, per l'azione ad esempio di un campo elettnco, in energia trasversale (di rivoluzione), in tutti i casi di interesse pratico in cui gli urti individuali delle singole particelle possano essere trascurati.

5. Configurazioni toroidali: confinamento a corrente diffusa

Le configurazioni toroidali di un plasma confinato in un campo magnetico hanno particolare importanza, sia perchè al momento attuale sembrano le più promettenti, in vista di una verifica sperimentale della realizzabilità scientifica di un reattore termonucleare, sia perché attraverso il loro studio si è giunti alla comprensione di processi fondamentali della fisica dei plasmi. In particolare consideriamo plasmi a basso β, in cui la densità di energia cinetica è molto più piccola di quella magnetica (β = 8πnkT/B²). Discuteremo nei dettagli la configurazione toroidale ‛a corrente diffusa' (v. Coppi e Rem, 1972), dati i progressi che sono stati fatti con tale tipo di confinamento magnetico negli ultimi anni; molte delle considerazioni che faremo si applicano altrettanto bene ad altre forme di confinamento.

La configurazione anzidetta consiste in un anello di pla sma di sezione circolare (v. fig. 7) immerso in un forte campo magnetico nella direzione toroidale, B_T, cui viene applicato un campo elettrico E_T, anch'esso in direzione toroidale, che genera una corrente totale I_T all'interno del plasma. Questa corrente a sua volta produce un campo magnetico poloidale B_p. La combinazione del campo B_p e del campo toroidale B_T genera linee di campo a forma di elica che giacciono su superfici magnetiche chiuse (fasci di superfici toroidali). Generalmente, quando si parla di configurazioni ‛a strizione' (comunemente chiamate pinches), ci si riferisce a situazioni in cui il plasma è sottoposto alla compressione da forze prodotte dalla corrente che vi viene indotta. La forza di compressione per unità di volume è data da j_T ⋀ B_p, dove j_T è la densità di corrente toroidale. Si tratta dello stesso tipo di forza che fa in modo che due fili paralleli si attraggano quando sono percorsi da correnti aventi lo stesso verso. Nelle configurazioni ‛a strizione' (sharp pinches) la corrente j_T lungo la colonna del plasma scorre in un sottile strato esterno. Al contrario, nelle configurazioni ‛a corrente diffusa' (diffuse pinches) la corrente è distribuita su tutta la sezione trasversale del plasma. I principali componenti per realizzare configurazioni a corrente diffusa consistono in un recipiente di forma toroidale in cui è posto il plasma, in una bobina per produrre il campo magnetico toroidale e in un trasformatore, per indurre il campo elettrico E_T del quale il plasma costituisce il secondario. Il recipiente in cui è posto il plasma si può considerare una camera a vuoto, in quanto le densità che interessano sono molto basse se paragonate a quelle di un gas a pressione e temperatura atmosferiche.

Un plasma in assenza di correnti non può rimanere in equilibrio in un campo magnetico toroidale, esattamente come un pallone a forma di toro senza tensione superficiale, che tenda a espandersi in ogni direzione, sia secondo il raggio minore r, sia secondo quello maggiore R. In presenza di una corrente toroidale l'equilibrio diventa possibile, poiché, in questo caso, l'espansione nella direzione radiale r è ostacolata dalla forza di contrazione per unità di volume j_T⋀B_p, mentre all'aumento del raggio R₀ si oppongono gli effetti dovuti a uno strato conduttore che circonda il plasma o a una forza j_TB_v associata a un campo magnetico verticale B_v opportunamente imposto. In assenza di un campo magnetico verticale, l'espansione causerebbe la compressione del campo poloidale B_p tra il plasma e l'involucro conduttore: nei tempi brevi, caratteristici degli esperimenti di contenimento di un plasma, il campo magnetico poloidale non riesce nè ad attraversare l'involucro nè a penetrare all'interno del plasma, dato che sono entrambi buoni conduttori. Il campo magnetico poloidale, così compresso, esercita sul plasma una forza che ne limita l'espansione in direzione di R. Per controllare direttamente la posizione del plasma, si applica un campo verticale anche quando un involucro di questo tipo sarebbe sufficiente a impedirne l'espansione.

La più importante instabilità macroscopica cui può andare incontro una configurazione a strizione distribuita è l'instabilità a serpentina (kink), che si manifesta quando la corrente nel plasma supera un certo valore, conosciuto come limite di Kruskal-Shafranov. Quando si raggiunge questo valore limite il campo magnetico poloidale è tale che una linea del campo attorno alla colonna del plasma si richiude su se stessa una sola volta dopo aver compiuto un giro. La colonna è quindi soggetta a spostamenti elicoidali che tendono a crescere (v. fig. 8) e che finiscono col distruggere la configurazione di equilibrio. In termini delle intensità dei campi magnetici poloidale e toroidale questo fenomeno si presenta quando il rapporto B_T/B_p diviene ugnale al rapporto tra il raggio maggiore e quello minore (rapporto di forma) R₀/α.

Oltre a quella menzionata, altri tipi di instabilità macroscopiche possono aver luogo in configurazioni toroidali a corrente diffusa (TCD). Con opportune distribuzioni di corrente all'interno del plasma si può tuttavia evitare che si verifichino, se (aB_T/R₀B_p) > q_s, dove q_s è il fattore di stabilità che si considera generalmente compreso tra 2,5 e 3. In pratica, a/R₀ è sempre minore di 1/3 e quindi la condizione suddetta si riduce a che B_p sia considerevolmente minore di B_T.

Come si è detto precedentemente, per valutare tutte le instabilità macroscopiche è sufficiente una teoria che consideri il plasma come un fluido conduttore, ignorandone l'aspetto particellare. Questo punto di vista non è più sufficiente alle alte temperature, tipiche dei plasmi termonucleari, quando il cammino libero medio per urto tra le particelle diviene maggiore delle dimensioni del sistema. Per illustrare un aspetto di questo problema consideriamo il moto di una particella carica nel campo magnetico di una configurazione toroidale a strizione distribuita. Come si è visto, dalla sovrapposizione di B_T e B_p si ottengono linee di campo magnetico a forma di elica che giacciono su di una superficie toroidale. Lungo una di queste linee l'intensità del campo magnetico varia, dato che B ≃ B_T ha una dipendenza da R del tipo 1/R (v. fig. 9), di modo che, seguendo la linea, si incontrano un massimo B_M e un minimo B_m d'intensità del campo magnetico a ogni giro intorno alla superficie magnetica. A causa di tale variazione d'intensità del campo magnetico, le particelle con bassa velocità lungo le linee di campo finiscono per restare intrappolate intorno a B_m, mentre quelle la cui componente della velocità nella direzione parallela è sufficientemente elevata non vengono intrappolate e si muovono lungo una linea di campo per tutta la sua lunghezza. Queste ultime particelle (circolanti) trasportano la corrente indotta dal campo elettrico.

La differenza tra particelle circolanti e particelle intrappolate può essere rappresentata proiettando il centro di rivoluzione di una loro traiettoria su una sezione trasversale. Nel primo caso si ha un cerchio completo lievemente spostato rispetto alla superficie magnetica; nel secondo una curva a forma di banana (v. fig. 10). È per questa ragione che il regime in cui si manifesta questa separazione delle particelle nelle due classi suddette prende il nome di regime ‛a banana'. In questo regime possono manifestarsi sia nuove instabilità sia nuove forme di trasporto di particelle e di energia attraverso il campo magnetico. Un aspetto preoccupante di questo regime è che, secondo la previsione teorica, le particelle con orbite a banana possono abbandonare il sistema attraverso un determinato meccanismo di instabilità. Gli esperimenti finora eseguiti sono giunti fin quasi al limite del regime ‛a banana' per gli elettroni, ma, per il momento, non si è trovata una prova chiara dell'insorgere di una simile instabilità.

Un'analisi teorica basata solo sugli effetti degli urti individuali mostra che la diffusione di particelle e di energia attraverso il campo magnetico non dipende da B_T, bensì da B_p, cioè dal campo generato dalla corrente. La principale funzione del campo toroidale B_T consiste perciò nell'impedire le macroinstabilità menzionate precedentemente e aumentarne l'intensità può solo produrre un effetto positivo per il contenimento del plasma, in quanto ciò permette di aumentare a sua volta il campo poloidale e quindi, nel caso di una configurazione a corrente diffusa, di aumentare la corrente. Questa è una caratteristica generale delle configurazioni toroidali e le esperienze finora eseguite l'hanno confermata.

6. Diffusione ‛classica', ‛neoclassica' e ‛anomala'

La diffusione di particelle e di energia attraverso il campo magnetico in un plasma, la resistenza elettrica, ecc., possono essere valutate con buona precisione tenendo conto soltanto dell'effetto degli urti individuali. I relativi coefficienti di trasporto vengono pertanto chiamati collisionali o ‛classici', per indicare che la loro natura è ben compresa. Per esempio, valutando su queste basi il coefficiente di diffusione delle particelle attraverso il campo magnetico nel caso di un plasma contenuto in un cilindro retto (v. fig. 2), si ha

D_el = ν_eiρ2_e,

in cui ν_ei è la frequenza d'urto elettrone-ione e ‛e il raggio di Larmor medio degli elettroni (ρ_e = v_t/Ω_e, con v_t velocità termica degli elettroni). L'espressione di D_el si ottiene considerando per gli elettroni un cammino casuale nel campo magnetico con passo medio uguale a ρ_e e frequenza ν_ei. Ne segue quindi che è D_el ∝ n/(Te^1/2B²) e che un plasma a temperatura elevata può essere contenuto facilmente all'interno di un forte campo magnetico.

Nel caso di una colonna di plasma toroidale, come quella indicata nella fig. 7, si trova che la diffusione è legata al cammino casuale dovuto agli urti delle particelle con orbite intrappolate intorno ai punti in cui il campo magnetico è minimo (v. Galeev e Sagdeev, 1968). I passi elementari di questo percorso casuale sono dati dai raggi delle orbite della banana, indicate nella fig. 10, la cui ampiezza è inversamente proporzionale al campo magnetico pobidale B_p. Il corrispondente coefficiente di diffusione, chiamato ‛neoclassico', è approssimativamente dato da

Questa espressione conferma che la diffusione derivante dagli urti individuali tra le particelle in una configurazione toroidale non è controllata dal campo magnetico toroidale, pur predominante, ma dal campo poloidale.

Osservazioni sperimentali su svariati metodi di confinamento hanno mostrato che effetti collettivi, quali microinstabilità, possono assumere un ruolo determinante nel trasporto di particelle e di energia attraverso il campo magnetico. Un caso di particolare importanza è la cosiddetta diffusione di Bohm, rappresentata dal coefficiente D_B ≃ (1/16)(cT_e/eB), che aumenta con la temperatura degli elettroni e non ha una forte dipendenza dal campo magnetico come nel caso della diffusione classica. Vari esperimenti effettuati con confignrazioni del tipo ‛stellarator' (v. cap. 9) hanno dimostrato così bene la presenza della diffusione di Bohm che a volte si è addirittura pensato che essa rappresentasse un aspetto inevitabile del contenimento toroidale.

Intorno alla prima metà degli anni sessanta si ottenne tuttavia un certo numero di risultati teorici che indicavano come si potessero chiamare in causa diverse microinstabilità per descrivere il manifestarsi, negli esperimenti citati, della diffusione di Bohm. Una gran parte di queste instabilità si verificava solo a condizione che il cammino libero medio di collisione delle particelle fosse più breve della lunghezza tipica delle linee del campo magnetico intorno al toro (v. Coppi e Rosenbluth, 1966). D'altra parte, lo stesso tipo di analisi teorica indicava che nei regimi con cammini liberi medi relativamente lunghi avrebbero dovuto manifestarsi mutamenti nelle caratteristiche del trasporto delle particelle e dell'energia attraverso il campo magnetico. Tale fatto, mentre implicava uno scostamento netto dalla diffusione di Bohm, prevedeva anche la possibilità di migliorare il contenimento del plasma. Queste previsioni teoriche furono fin dall'inizio confermate da tutta una serie di esperienze condotte con apparecchiature multipolari (aventi conduttori interni per il trasporto della corrente necessaria per generare il campo magnetico poloidale, di cui si dirà nel cap. 16) e con apparecchiature a corrente diffusa (v. cap. 8).

Così all'inizio degli anni settanta il problema essenziale delle ricerche sulla fusione e della fisica dei plasmi cominciò a non essere più quello del contenimento, ma quello del riscaldamento fino a temperature termonucleari.

Il passaggio dalla diffusione di Bohm a una in cui il tempo di confinamento aumenti con la temperatura è mostrato nella fig. 11. L'apparecchiatura ST ivi indicata è nata dalla conversione del grande Stellarator di Princeton in una configurazione a corrente distribuita.

Gli esperimenti più recenti, a cominciare da quelli effettuati nel 1974 con la macchina Alcator del MIT, hanno mostrato che il tempo di confinamento dell'energia tende a obbedire a una legge di scala, aumentando al crescere della densità delle particelle. Per questo abbiamo riportato nella fig. 12 i risultati di un'analisi svolta da Coppi e Mazzucato (v., 1971) riferendoli ai maggiori esperimenti in plasmi toroidali attualmente in corso. In particolare il coefficiente di diffusione dell'energia termica che porta a riprodurre i profili di temperatura ottenuti negli esperimenti è

ove ε_D ≃ 2 × 10^-3 è un coefficiente numerico, Ω_θe = eB_p(r)/m_ec è la frequenza di ciclotrone degli elettroni nel campo B_p(r) prodotto dalla corrente nel canale di raggio r,

Y_e = (D_ηω_pi/vt2_t)^2/5T_e

è una funzione debole della variabile spaziale e D_η = ηc²/4π è il coefficiente di diffusione resistiva del campo magnetico.

Le implicazioni del fatto che il tempo di confinamento dell'energia degli elettroni τ_e cresce con la densità sono varie. In particolare il parametro nτ_e, che è importante per la prova di fattibilità di un reattore a fusione, tende ad avere la dipendenza nτ_e ∝ n²a². Perciò è possibile realizzare alti valori di nτ_e non solo in esperimenti con grandi dimensioni, cioè caratterizzati da grandi valori di a², ma anche in esperimenti con piccole dimensioni e alte densità.

Sulla base di questa e di altre considerazioni, è stata suggerita una linea di esperimenti compatti, i cosiddetti ‛Ignitor', per lo studio del riscaldamento di un plasma, composto di deuterio e trizio, mediante particelle α da 3,5 MeV prodotte nelle reazioni di fusione. Poiché i valori di nπ_e previsti sono vicini a quelli richiesti per la prova di fattibilità di un reattore a fusione, con questi tipi di esperimenti è possibile in linea di principio studiare le condizioni nelle quali ci si avvicina all'¹accensione', cioè al regime in cui tutte le perdite di energia da parte del plasma sono compensate dal riscaldamento del plasma dovuto al rallentamento nel plasma stesso delle particelle α s0pracitate.

7. Il problema del riscaldamento

Il modo più semplice per riscaldare un plasma prodotto in un esperimento di contenimento toroidale consiste nello sfruttare la resistenza elettrica che il plasma presenta al passaggio della corrente. Tale tipo di riscaldamento è detto ohmico. Non è ancora chiaro quali siano i suoi limiti. Infatti questi sono attualmente oggetto di indagine al MIT di Cambridge e nei laboratori di Frascati, con le apparecchiature Alcator C ed FT, rispettivamente, e in diversi piccoli esperimenti di ricaldamento turbolento.

La resistenza di un plasma può essere dominata da effetti collisionali o da effetti collettivi; consideriamo il primo caso, che è abbastanza ben conosciuto.

Se si applica un campo elettrico E_T nella direzione di quello magnetico B_T, gli elettroni tendono ad acquistare quantità di moto nel verso opposto al campo E_T e gli ioni nel verso concorde. Gli elettroni, avendo massa minore, tenderanno ad acquistare velocità maggiori, in valore assoluto, di quelle degli ioni e quindi a portare la maggior parte della corrente; tuttavia ne' gli elettroni nè gli ioni sono accelerati liberamente, a causa degli urti attraverso i quali si scambiano quantità di moto rallentandosi reciprocamente; nasce in tal modo una resistenza.

Tale resistenza collisionale (v. Spitzer, 1962) è una funzione che decresce molto rapidamente con la temperatura degli elettroni ed è numericamente data da

ove Z è la carica degli ioni in unità elettroniche e T~ la temperatura degli elettroni espressa in keV; quindi, se si prendono in considerazione solo gli urti tra elettroni e ioni, un plasma alla temperatura di i keV dovrebbe presentare circa la stessa resistenza del rame a temperatura ambiente.

La potenza termica generata dalla corrente è data da P₁ = (2π²a²R₀)η_II j2_T, in cui η_II è la resistenza del plasma lungo il campo magnetico. La densità di corrente si può esprimere nella forma

con j_T in ampere/cm², B_T in gauss ed R₀ in centimetri; P_t si può pertanto riscrivere nella forma

Ne consegue che, se la resistenza η_el di un plasma è uguale semplicemente alla resistenza collisionale η_el la potenza trasferita dal trasformatore al plasma diminuisce sensibilmente al crescere della temperatura elettronica (a, R₀ e B_T sono fissi per una data apparecchiatura e q_s è limitato per ragioni di stabilità; v. cap. 5) e quindi per ottenere temperature più elevate di quelle ottenute finora è importante trovare meccanismi di riscaldamento la cui efficacia presenti una dipendenza dalla temperatura più favorevole di quella presentata dall'effetto Joule derivante dalla resistenza collisionale.

Un tale meccanismo può essere per esempio il trasferimento turbolento di quantità di moto dagli elettroni agli ioni che si verifica in condizioni di alta densità di corrente. Queste condizioni vengono realizzate in due modi principali: in condizioni stazionarie, con valori relativamente alti del campo magnetico B_T e bassi valori della lunghezza 2πR₀ della colonna di plasma, oppure in condizioni transienti, dando un fortissimo impulso di campo elettrico, della durata di alcuni microsecondi. Questo impulso produce una forte turbolenza, anche macroscopica, la quale non impedisce che successivamente la scarica si stabilizzi e perduri nel tempo.

A questo punto si devono fare due osservazioni: la prima è che la presenza nel plasma di impurezze pesanti come ferro o molibdeno aumenta la Z che compare al numeratore dell'espressione della resistenza η_el e quindi, per poter rivelare fenomeni non classici in un plasma di idrogeno, bisogna prestare molta attenzione alla purezza del plasma; la seconda è che la forma numerica della η_el è stata calcolata supponendo che la funzione di distribuzione degli elettroni nello spazio delle velocità avesse una forma ben determinata, detta di Spitzer e Härm; questa ipotesi è valida quando il valore del rapporto tra la velocità degli elettroni associata alla corrente, v_D = − j/ne, e la loro velocità termica

è molto piccolo (ξ = v_D/v_T > 0,02). Per valori più grandi del parametro di flusso ξ la funzione di distribuzione elettronica può essere significativamente diversa da quella di Spitzer e Härm e la resistenza minore di η_el; questo fatto può mascherare l'aumento di resistenza dovuto alla turbolenza.

Accanto a quello ohmico, classico o turbolento che sia, esistono vari sistemi di riscaldamento ausiliario. Quello fino a oggi più largamente sperimentato consiste nell'iniettare un fascio di atomi neutri molto energetici nella colonna di plasma. Gli atomi neutri, una volta iniettati, vengono ionizzati, si propagano lungo il campo magnetico e trasferiscono la loro energia alle particelle del plasma di fondo.

La tecnologia degli iniettori di neutri è in via di sviluppo, in quanto, per riscaldare un plasma con valori sufficientemente elevati del parametro di confinamento nτ_e (v. cap. 16), sono necessarie energie degli atomi neutri (circa 200 keV) molto superiori a quelle attualmente raggiungibili (circa 40 keV). Nella fig. 13 è rappresentato schematicamente un apparato per iniezione di neutri. Gli esperimenti in cui viene attualmente impiegato questo sistema di riscaldamento sono diversi; ricordiamo tra quelli a corrente diffusa il TFR di Fontenay aux Roses in Europa e il PLT di Princeton, dove sono state raggiunte le temperature ioniche più elevate. Il tipo di macchina in cui questo sistema di riscaldamento ha avuto un ruolo essenziale è quello a specchi magnetici (v. cap. 12).

Un modo completamente differente di affrontare il problema consiste nel riscaldare una colonna di plasma comprimendola adiabaticamente. Seguendo tale principio si è riusciti, a Princeton, con l'espenmento ATC, a comprimere un plasma toroidale riducendone simultaneamente i raggi maggiore e minore da 2,5 a 3 volte.

Una tecnica ancora diversa di riscaldamento ausiliario consiste nel fare assorbire al plasma energia sotto forma di onde elettromagnetiche. In questo caso si usano frequenze che variano, a seconda del tipo di risonanza del plasma che si sfrutta, da 1 kHz (frequenza di transito degli ioni) a centinaia di GHz (frequenza di ciclotrone degli elettroni). A seconda della frequenza scelta i problemi da affrontare cambiano radicalmente.

In corrispondenza con le frequenze di transito degli ioni esistono generatori molto potenti e l'antenna che li accoppia al plasma può essere situata al di fuori della camera a vuoto; attualmente l'efficienza di accoppiamento è bassa (dell'ordine dello 0,1%), ma si prevede che aumenti passando a plasmi più caldi e densi di quelli sui quali è stata finora sperimentata.

Con la frequenza delle onde di Alfvén (1 MHz) e di ciclotrone ionica (100 MHz) si debbono usare antenne interne alla camera metallica del plasma.

La frequenza ibrida inferiore (ω_LH ≃ √-Ω-_o-Ω-_ci) rientra nel campo delle microonde e quindi si possono usare guide d'onda per l'accoppiamento tra il generatore e il plasma. Le tecnologie per i generatori in questa banda di frequenze sono soddisfacenti sia per le potenze che per i rendimenti.

Alle più alte frequenze usate, cioè alla prima o alla seconda armonica della frequenza di ciclotrone degli elettroni, le proprietà del plasma sono meglio controllabili perché le lunghezze d'onda sono molto più piccole delle dimensioni del plasma stesso e quindi la penetrazione della radiazione può essere studiata con le tecniche matematiche dell'ottica geometrica, ma la tecnologia relativa ai generatori dev'essere ulteriormente sviluppata.

In un plasma di deuterio-trizio che abbia raggiunto temperature superiori a 4 keV, l'energia fornita al plasma dal rallentamento delle particelle da 3,5 MeV generate nelle reazioni di fusione diventa la forma più importante di riscaldamento quanto più ci si avvicina alle condizioni di accensione termonucleare (v. cap. 16).

Va notato infine un altro aspetto della dipendenza dalla temperatura - o meglio dal suo profilo nella direzione perpendicolare alle superfici magnetiche della resistività classica e della conducibilità termica dovuta agli urti degli elettroni, secondo cui si dovrebbe formare una corrente superficiale pellicolare. Dai calcoli effettuati con questi coefficienti di trasporto segue che la densità di corrente dovrebbe avere un massimo molto pronunciato vicino ai bordi del plasma (v. fig. 14) per tempi relativamente lunghi; un andamento dello stesso tipo si avrebbe per la temperatura degli elettroni. In tutti gli esperimenti, tuttavia, si è trovato che la densità di corrente diventa rapidamente una funzione che decresce lentamente con il raggio e ciò conferma che la distribuzione della densità di corrente non è controllata da effetti collisionali.

8. Esperimenti toroidali a corrente diffusa

La possibilità di produrre plasmi di interesse termonucleare in una configurazione a corrente diffusa è emersa in seguito ai risultati ottenuti nelle esperienze eseguite all'Istituto Kurchatov di Mosca con una serie di apparecchiature dette Tokamak (v. Artsimovich, 1972).

I principali componenti di questo tipo di apparecchiatura sono: una camera a vuoto metallica di forma toroidale, un magnete costituito da spire avvolte attorno ad essa, un trasformatore a nucleo di ferro o d'aria, il cui secondario è costituito dalla colonna di plasma contenuta nella camera toroidale, e una scocca conduttrice o delle bobine per generare un campo verticale. Spesso è presente anche un diaframma per limitare il raggio della scarica ed evitare che questa lambisca le pareti interne della camera toroidale. Il diaframma è costituito da un anello ad alta temperatura di fusione.

Nelle macchine toroidali a corrente diffusa il plasma viene prodotto nel modo seguente: si introduce nella camera a vuoto idrogeno (o deuterio) gassoso fino a raggiungere una pressione di circa 10^-4 torr. Una volta raggiunto il valore di pressione prestabilito, viene fatta passare nel primario del trasformatore una corrente che varia in modo tale da indurre nel gas un campo elettrico che inizialmente è molto intenso, per cui causa nel gas una ionizzazione a valanga, e poi si mantiene a livelli più bassi, sufficienti a sostenere la corrente creata all'inizio, che confina e riscalda il plasma. Per tutta la durata della scarica, che può variare da alcuni decimi di secondo ad alcuni secondi, il campo magnetico toroidale viene mantenuto a un valore costante.

Dagli inizi degli anni settanta, visti i promettenti risultati e la relativa semplicità degli esperimenti effettuati con configurazioni a corrente diffusa, si è avuta in tutto il mondo una vasta proliferazione di questo tipo di macchina. Questo ha permesso di esplorare un'ampia gamma di valori dei parametri che determinano le proprietà del plasma e quindi, da una parte, di formulare leggi di scala fenomenologiche per i processi di perdita delle particelle e dell'energia termica e, dall'altra, di identificare i processi fisici che le giustificano e ne indicano i limiti di validità.

Il primo grande passo, compiuto con i Tokamak T-3 e T-4 a Mosca, è stato la verifica che, in regimi di alta temperatura, il coefficiente di diffusione dell'energia non è nè per l'ordine di grandezza nè per la dipendenza dai vari parametri del plasma rappresentato dal coefficiente empirico di Bohm (v. cap. 6).

Altri fatti importanti messi in evidenza in quegli esperimenti sono stati i seguenti: a) il limite superiore che si può ottenere per la corrente di plasma è quello di Kruskal-Shafranov (v. cap. 5), avvicinandosi al quale insorge l'instabilità a serpentina (v. Coppi e Rem, 1972); in particolare si sono ottenuti recentemente valori del parametro di sicurezza q inferiori a 2, senza perdita di contenimento del plasma; b) il trasferimento di energia dagli elettroni agli ioni avviene per urti, cioè non coinvolge microinstabilità; analogamente la conducibilità termica ionica è coerente con quella prevista dalla teoria classica del trasporto, dovuta a collisioni ione-ione; c) la penetrazione del campo poloidale nella colonna di plasma è anomala, perché non si verifica il forte ‛effetto pelle' prevedibile in base all'alta conducibilità del plasma.

In seguito sono state costruite in tutto il mondo diverse macchine toroidali a corrente diffusa, con le quali si sono fatti e si stanno facendo grandi progressi, grazie anche alle tecnologie d'avanguardia impiegate sia nella costruzione che nei sistemi diagnostici.

Alcator A (v. fig. 15) è stato il primo esperimento della generazione successiva ai Tokamak russi che sia entrato in funzione. Inizialmente concepito per produrre alte temperature degli elettroni con densità relativamente basse (2,5 × 10¹⁴ cm^-3) e riscaldamento puramente chimico, ha permesso di identificare fenomeni nuovi e inattesi, grazie alla grande purezza del plasma prodotto (bassa concentrazione di elementi con Z > 1) e all'assenza di elettroni relativistici, nonché alla possibilità di variare ampiamente la densità e la corrente di plasma.

Si è scoperto in primo luogo che nei regimi a bassa densità inizialmente esplorati la funzione di distribuzione degli elettroni si discostava significativamente da quella di un plasma termico (che è una maxwelliana cui è sovrapposto un termine detto di Spitzer e Härm sbilanciato nel verso della corrente), per cui la resistività tendeva a diminuire rispetto a quella classica, mentre, quando il parametro di flusso ξ (v. cap. 7) superava un dato valore di soglia, veniva prodotto un nuovo regime. In questo regime, detto di slide-away (v. Boxman e altri, 1975), si sono manifestati e rivelati con inaspettata chiarezza fenomeni di trasferimento dell'energia dagli elettroni agli ioni, dovuti a effetti collettivi.

Aumentando la densità e uscendo da questo regime si è scoperto che il tempo di confinamento dell'energia elettronica aumentava proporzionalmente alla densità (come si è già indicato nel cap. 6). L'importanza di questa circostanza è aumentata dal fatto che la penetrazione delle particelle nella scarica è anomala, cioè, soffiando impulsi di gas con una valvola piezoelettrica durante la scarica, non si forma una zona di plasma freddo sul bordo della colonna di plasma, ma la densità cresce su tutta la sezione. Questo fatto ha permesso di raggiungere in Alcator valori del parametro di confinamento nτ_e pari a 3 × 10¹³ cm^-3s, quali non sono stati ancora uguagliati in alcun altro esperimento.

Ispirato a una concezione opposta a quella dell'Alcator è il PLT (v. fig. 16), di grandi dimensioni e con densità di corrente relativamente piccola. In questa macchina si sono ottenute temperature ioniche T_i = 6 keV mediante riscaldamento per iniezione di atomi neutri energetici, entrando cosi in un regime ‛a banana' (v. cap. 6) anche per gli ioni.

Molti altri risultati, meno spettacolari ma altrettanto importanti, sono stati ottenuti in questi e in altri esperimenti.

1. Si sono ottenute scariche che terminano senza violente disrupzioni, dovute a instabilità macroscopiche del plasma, e quindi senza indurre forti extratensioni nei circuiti di alimentazione delle bobine. Il controllo completo di questi fenomeni è essenziale per gli esperimenti della prossima generazione (v. cap. 11), nei quali si avranno correnti di milioni di ampere, quali sono richieste per il confinamento delle particelle a da 3,5 MeV prodotte nelle reazioni di fusione deuterio-trizio.

2. Sono stati sviluppati diversi metodi per l'eliminazione delle impurezze, cioè di ioni diversi da quelli del plasma di base. Tale ‛pulizia' è indispensabile per poter arrivare all'accensione di un reattore a fusione e anche perché la presenza di impurezze influenza in modo importante le proprietà di trasporto di un plasma e quindi, come è già avvenuto nella fisica dello stato solido, è necessario eliminarle per poter trarre indicazioni generalizzabili.

Il metodo più largamente usato è quello delle scariche di pulizia, costituite da piccoli impulsi di corrente ripetuti a distanza di uno o più secondi, che preparano la camera a vuoto e il diaframma; il loro effetto più importante è quello di eliminare l'ossigeno adsorbito dall'acciaio. Un'altro sistema impiegato per l'eliminazione delle impurezze leggere consiste nell'evaporazione di uno strato di titanio sulle pareti.

Per l'eliminazione delle impurezze pesanti si usano diaframmi costituiti da carbonio o acciaio inox in luogo di materiali più pesanti, oppure si cerca di produrre un mantello di gas freddo attorno alla colonna di plasma. In alcuni esperimenti viene impiegato un ‛divertore magnetico', costituito da un sistema di magneti che modificano la geometria del campo all'interno della camera toroidale, in modo tale che da un certo raggio in poi le linee di campo passino in una camera a vuoto ausiliaria, dove possono essere intercettate da un diaframma senza che gli ioni emessi da quest'ultimo vadano a inquinare il plasma.

Dato che la presenza di una sia pur piccola quantità di impurezze non sarà mai eliminabile completamente, è necessario conoscerne bene la dinamica e gli effetti; per questo il problema è oggetto di studio in diversi esperimenti.

3. Tramite misure di diffusione (scattering) di microonde è stato possibile rilevare la presenza di fluttuazioni, identificabili come onde di deriva (v. cap. 15), le quali dovrebbero permettere di arrivare a riconoscere la natura dei modi collettivi da cui dipendono i fenomeni di diffusione anomala dell'energia termica degli elettroni e delle particelle, già discussi nel cap. 6.

4. Si sono ottenuti risultati incoraggianti nei tentativi fatti per alzare il più possibile il rapporto β del plasma, usando scariche con sezioni non circolari ed effettuando un accurato controllo delle salite in corrente e delle densità di plasma. I massimi valori si sono ottenuti con le macchine T-11 di Mosca e ISX di Oak Ridge.

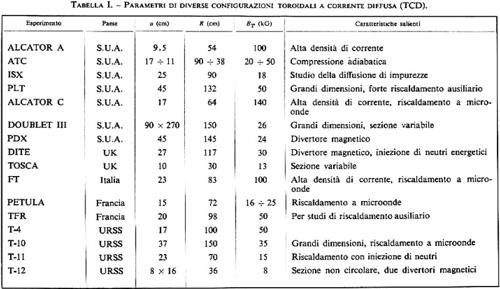
Nella tab. I sono riportati i parametri di diverse macchine TCD fra cui ricordiamo le più avanzate: l'Alcator A, di piccole dimensioni, alti campi magnetici (B_T ≤ 100 kG) e alte densità di corrente; l'Alcator C, che sta ora entrando in funzione, più grande del precedente e con forte riscaldamento a microonde; il PLT (Princeton), di grandi dimensioni e con un campo magnetico relativamente basso, con forte riscaldamento per iniezione di neutri energetici; il Doublet III (San Diego), di grandi dimensioni, capace di produrre scariche con sezioni fortemente non circolari e correnti fino a 3 MA; il DITE (Culham) con divertore magnetico e forte riscaldamento con neutri energetici; l'FT (Frascati; v. fig. 17) con alto campo e dimensioni relativamente grandi; il T-10 (Mosca), di grandi dimensioni e con riscaldamento per risonanza alla frequenza di ciclotrone degli elettroni.

9. La configurazione stellarator

Uno ‛stellarator' è una configurazione toroidale con una componente toroidale B_T del campo magnetico prodotto da un sistema di bobine simile a quello impiegato nella configurazione a corrente diffusa. In esso sia la trasformata rotazionale (definita nella fig. 18) che lo ‛svergolamento' delle linee di forza del campo magnetico sono prodotti da un avvolgimento multiplo a forma di elica che gira tutt'intorno alla colonna del plasma, come è mostrato nella fig. 19. Ricordiamo che per ottenere tale effetto nel caso della configurazione toroidale a corrente diffusa si usa la corrente indotta nel plasma stesso. In questo senso la configurazione stellarator è più flessibile, poiché il riscaldamento Joule dovuto alla corrente di plasma J_T è disaccoppiato dalla configurazione magnetica che provvede al contenimento ed è quindi adatto a operare in condizioni stazionane. Gli svantaggi sono, peraltro, rappresentati dal fatto che uno stellarator è una configurazione intrinsecamente tridimensionale: non presenta simmetria toroidale ed è quindi più difficile da analizzare teoricamente e notevolmente più complesso da costruire. Di fatto, una configurazione toroidale a corrente diffusa (TCD), grazie alla sua maggiore semplicità tecnica, si presta a svariate realizzazioni sperimentali che permettono di accedere con facilità al plasma, di applicare campi magnetici intensi, ecc.

Le ricerche sulle configurazioni stellarator, iniziate all'Università di Princeton, furono abbandonate nel 1970 a favore delle configurazioni TCD. D'altra parte questa linea di ricerca fu intrapresa ed è tuttora perseguita in laboratori della Gran Bretagna, della Germania, del Giappone e dell'Unione Sovietica.

Finora il più grande e più avanzato esperimento con una configurazione stellarator è stato effettuato con l'apparecchiatura Wendelstein VII, attualmente in funzione nei laboratori di Garching presso Monaco. I principali parametri del progetto originale sono: raggio maggiore del plasma R = 200 cm, raggio minore a variabile da 20 a 34 cm, campo magnetico toroidale (sull'asse) B_T = 40 kG.

10. Multipoli toroidali

Si chiamano comunemente ‛multipoli' (v. fig. 20) le configurazioni toroidali nelle quali il campo magnetico di contenimento viene prodotto da correnti che scorrono entro conduttori metallici posti all'interno del plasma: i multipoli presentano simmetria toroidale e, al contrario delle configurazioni TCD, permettono di disaccoppiare il processo di riscaldamento dalla configurazione magnetica di contenimento.

Attrezzature sperimentali con un numero differente di anelli all'interno sono state già messe a punto (v. fig. 21) ed è stato possibile ricavare una gran quantità di informazioni di base sulla fisica del contenimento di un plasma. Tra i vari risultati ottenuti vanno ricordati: la prima prova sperimentale chiara che la diffusione di Bohm non è una caratteristica dei plasmi a contenimento toroidale; l'osservazione dell'insorgere nel plasma di modi di oscillazione causati dalla presenza di particelle intrappolate; l'osservazione del cambiamento (v. Ohkawa, 1972) che si verifica nel processo di diffusione collisionale delle particelle (v. cap. 6) al passare da un regime in cui la frequenza di collisione è più grande della frequenza di transito delle particelle lungo le linee del campo magnetico a uno in cui sono dominanti gli effetti dovuti alle particelle intrappolate (corrispondente al regime a banana di cui si è parlato precedentemente), le quali, in queste condizioni, rimbalzano con una frequenza maggiore di quella collisionale (v. fig. 22). Nella fig. 20 è riportato lo schizzo di una configurazione lineare a ottupolo e le linee del campo magnetico indicate corrispondono al caso in cui non si è applicato alcun campo lungo l'asse della configurazione, mentre la fig. 21 si riferisce a una situazione in cui vi è un campo magnetico assiale tale da far muovere le particelle su orbite con una escursione radiale periodica, maggiore del raggio di rivoluzione intorno alle linee di campo.

11. La prossima generazione di esperimenti con plasmi termonucleari

Gli esperimenti attualmente in corso su plasmi toroidali stanno fornendo un complesso di informazioni in base alle quali si possono identificare parametri che potrebbero caratterizzare un reattore a confinamento magnetico. Tali parametri hanno un largo margine di incertezza, dato che i coefficienti di trasporto del plasma sono noti soltanto per regimi diversi da quelli per i quali ci si attende di poter arrivare all'ignizione (v. cap. 16) o che comunque possono condurre a condizioni di produzione netta di energia da fusione.

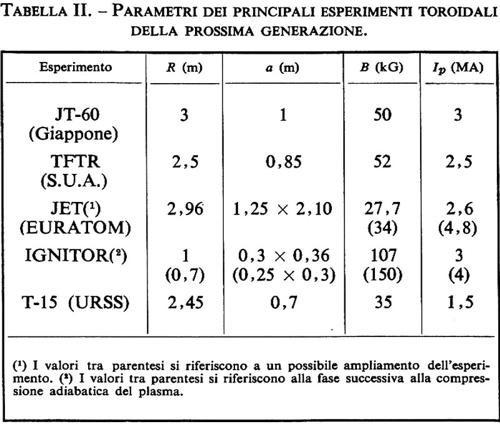
L'entrata in funzione delle principali macchine della prossima generazione è prevista per la prima metà degli anni ottanta. Nella tab. II sono indicati i principali parametri caratteristici di tali esperimenti.

Come per gli esperimenti della generazione attuale, così per quelli della prossima si possono distinguere due linee di ricerca: una orientata verso plasmi di grandi dimensioni confinati da campi magnetici relativamente bassi (JET, TFTR, JT-60) e l'altra verso dimensioni più piccole e campi magnetici piu intensi (Ignitor). Infatti la prima macchina per arrivare all'ignizione è stata proposta proprio su quest'ultima linea, in base ai risultati ottenuti con l'esperimento Alcator, già descritto nel cap. 8.

Le condizioni da soddisfare perché il plasma si autoriscaldi, oltre a quella relativa alla temperatura (v. cap. 16), sono due; entrambe possono essere, in linea di principio, soddisfatte sia in esperimenti di grandi dimensioni che in esperimenti compatti. La prima è che il parametro di confinamento nτ superi un certo valore (v. cap. 16) e la seconda che la maggior parte delle orbite delle particelle α prodotte nelle reazioni di fusione sia confinata all'interno del plasma; questa condizione si può tradurre in una condizione per la corrente totale che fluisce negli avvolgimenti del magnete: I_c ≥ 7 Aq_s megampere-spire, ove A è il rapporto di aspetto e q_s il fattore di stabilità (v. sopra, cap. 5). In questo modo si vede che la condizione in questione è indipendente dalle dimensioni dell'esperimento, in quanto può essere soddisfatta sia adottando magneti toroidali di dimensioni relativamente piccole con campi magnetici molto intensi, sia in una configurazione grande, con campo magnetico meno intenso. La prima condizione si può riscrivere in termini del prodotto n²a², tenendo conto del fatto che negli esperimenti svolti finora si è trovato che il tempo di contenimento dell'energia è proporzionale a na² (v. cap. 6); anche in questo caso esistono due vie indipendenti per avvicinarsi al valore di nτ richiesto: aumentare a², cioè la sezione del plasma, o aumentare la densità n; si è visto che quest'ultima possibilità è realizzabile in plasmi compatti e confinati da forti campi magnetici.

Sulla linea degli esperimenti compatti sono situabili diverse macchine di tipo ‛Ignitor' (v. fig. 23), dal nome della prima macchina di questo tipo per la quale i parametri principali sono stati definiti nella tab. II.

Tali esperimenti offrono la possibilità di studiare il comportamento di un plasma fortemente riscaldato da particelle a prodotte in reazioni di fusione, affrontando spese e tempi di realizzazione molto minori di quelli necessari per le grandi macchine precedentemente indicate. In particolare l'Ignitor è stato concepito per funzionare con densità di plasma dell'ordine di 10¹⁵ cm^-5, di un ordine di grandezza più grandi di quelle previste ad esempio per il JET; quindi, anche alla temperatura di ignizione, il plasma si troverà in regimi di collisionalità (v. cap. 6) già esplorati con gli esperimenti della generazione attuale. Questo permette di prevedere la forma che avranno i coefficienti di trasporto delle particelle e dell'energia termica nel plasma meglio che per i regimi di bassa collisionalità a cui funzioneranno le grandi macchine, perché non si ha una sufficiente conoscenza dei fenomeni collettivi che potrebbero insorgere a quei regimi.

D'altra parte, dati i valori di densità di plasma che caratterizzeranno l'Ignitor, non sarà possibile usare riscaldamento ausiliario con neutri energetici come è previsto per le grandi macchine; il riscaldamento ohmico (molto forte grazie all'alta densità di corrente) sarà complementato da compressione adiabatica ed eventualmente da riscaldamento a microonde (v. cap. 7).

Riferendoci agli esperimenti di grandi dimensioni (v. Bickerton, 1979) ricordiamo che il JT-60 (v. tab. II) è stato progettato per raggiungere i parametri di plasma che sono considerati sufficienti per avere ignizione senza però immettere trizio. Pertanto lo studio di problemi quali il confinamento e il rallentamento delle particelle a prodotte in reazioni di fusione D-T non può essere affrontato in tale esperimento.

Il TFTR è stato progettato per funzionare con trizio. In tal caso si prevede di ottenere dal plasma tanta energia da reazioni termonucleari quanta ne è fornita mediante iniezione di atomi neutri energetici (verrà iniettato deuterio in un plasma di trizio). Tale obiettivo sarà perseguito nel regime detto a due componenti, nel quale la resa neutronica dipende soprattutto dall'energia degli atomi neutri iniettati. Dato il basso rendimento energetico totale del sistema a due componenti, si prevede che il suo uso debba rimanere limitato a soli scopi dimostrativi.

Il JET (v. fig. 24) è la più grande tra le macchine di prossima attuazione. Tra i suoi obiettivi più ambiziosi vi è quello di raggiungere temperature fino a 10 keV, per poter studiare l'interazione tra plasmi caldi e le pareti della camera toroidale, i processi di trasporto in regimi di bassa collisionalità (v. cap. 6), i massimi valori ottenibili per il parametro β e, infine, gli aspetti più caratteristici dei plasmi di deuterio e trizio.

Tra gli esperimenti di grandi dimensioni ricordiamo infine il T-15, che verrà realizzato nell'Unione Sovietica. Il progetto di questa macchina prevede l'impiego di un magnete superconduttore per produrre il campo magnetico toroidale e di impianti per il riscaldamento ausiliario del plasma con iniezione di atomi neutri energetici e con onde elettromagnetiche alla frequenza di ciclotrone degli elettroni.

12. Geometrie a estremi aperti: specchi magnetici

I sistemi a specchi magnetici rappresentano uno dei principali metodi per contenere un plasma. Nella fig. 25 è rappresentata la configurazione più semplice di questo tipo: essa consiste di una colonna aperta di plasma in cui il campo magnetico aumenta in corrispondenza delle estremità. L'intensificarsi del campo incurva le traiettorie delle particelle, che si avvicinano in circonferenze sempre più strette, ed esercita una forza che finisce con il produrre la riflessione delle particelle dalle estremità della colonna. La presenza intorno alla Terra delle fasce di Van Allen è un'ottima prova della possibilità di contenere particelle con specchi di questo tipo. D'altra parte la configurazione descritta nella fig. 25 va incontro a instabilità macroscopiche di scambio del tipo di quelle descritte nel cap. 3. Per eliminare tale forma di instabilità bisogna aggiungere alle bobine di base dello specchio un altro sistema di spire, si da creare un opportuno campo magnetico che aumenti in tutte le direzioni allontanandosi dal centro della regione di confinamento. Nella fig. 26 sono indicati i profili delle superfici magnetiche di questa configurazione e la spira ‛a cucitura di palla da tennis' che la produce (v. Fowler e Post, 1966).

Nonostante fosse stata indicata teoricamente parecchi anni prima, la prima prova sperimentale della realizzabilità di questa configurazione non si ebbe che nel 1961, quando M. S. Joffe e i suoi collaboratori all'Istituto Kurchatov di Mosca dimostrarono che si otteneva così un notevolissimo miglioramento nel contenimento del plasma.

Da allora il principale obiettivo di ricerca, nello studio degli specchi magnetici, fu quello di trovare un metodo per eliminare sia le varie forme di microinstabilità responsabili di un'ulteriore diffusione delle particelle, oltre a quella dovuta agli urti individuali, sia le perdite alle estremità aperte del sistema. Un progresso continuo in tale campo ha fatto sì che nell'apparecchiatura sperimentale 2X-IIB, realizzata al Livermore Laboratory dell'Università di California, si siano ottenuti plasmi con densità dell'ordine di 2 × 10¹⁴ cm^-3, tempi di contenimento di circa 0,5 ms e temperature ioniche di circa 14 keV.

La fig. 27 mostra una versione migliorata dell'apparecchiatura 2X, chiamata 2X-II. Il pregio delle configurazioni in cui si fa uso di specchi sta nel fatto che esse sono più facili da studiare rispetto a quelle toroidali, sia sul piano teorico che su quello sperimentale. Inoltre in linea di principio un reattore a fusione a specchi (v. cap. 16) potrebbe venir progettato in dimensioni relativamente ridotte rispetto a quelle che vengono generalmente prese in considerazione per sistemi toroidali. Ricordiamo infine che sono in via di sviluppo nuove configurazioni di confinamento che impiegano una coppia di specchi (‛tandem di specchi') alle estremità di una colonna cilindrica di plasma.

13. Sistemi lineari e toroidali con β finito

Le configurazioni precedentemente descritte sono state realizzate nella maggior parte dei casi per ottenere plasmi con valori relativamente bassi del parametro β = 8πnk(T_e + T_i)/B². Può essere utile ricordare che il parametro β dà anche una valutazione dell'efficienza con cui il campo magnetico viene utilizzato per confinare un plasma di data pressione. In particolare, studi sulla possibilità di realizzare un reattore ‛economico' (v. cap. 16) indicano che è necessario ottenere valori medi di β che superino il 5 ÷ 10%.

Esistono diversi sistemi caratterizzati dall'avere densità di energia cinetica del plasma dello stesso ordine di grandezza della densità dell'energia magnetica. La più semplice apparecchiatura sperimentale di questo tipo viene detta ‛a corrente azimutale' (o theta-pinch, perché con θ si suole indicare la coordinata azimutale). Il suo modo di funzionare è il seguente: un gas ionizzato (generalmente deuterio) viene posto in un solenoide formato da una sola spira attraverso cui si fa passare bruscamente, in direzione azimutale, la corrente fornita da un condensatore; di conseguenza, nello spazio all'interno del solenoide insorge rapidamente un campo magnetico parallelo all'asse, che spinge verso l'interno la superficie del plasma producendo un'onda d'urto e quindi un riscaldamento degli ioni e degli elettroni. A questa fase ne segue una di quiescenza, nella quale il campo magnetico nel solenoide si stabilizza su un valore costante. In questa situazione il plasma è confinato in una configurazione a forma di sigaro dalle cui estremità esso sfugge gradualmente lungo le linee magnetiche, indicate da una freccia nella fig. 28.

Finora con configurazioni di tipo theta-pinch si è giunti a temperature di circa 5 keV, densità di 10¹⁶ ÷ 10¹⁷ particelle/cm³ e tempi di contenimento dell'ordine di 10 microsecondi. Si è accertato che i tempi di contenimento sono limitati a tali valori dalle perdite delle particelle dalle estremità (v. Ribe, 1972). Si è perciò rivolta l'attenzione verso versioni toroidali del theta-pinch; la più grande di queste macchine è la Scyllac, installata presso i laboratori di Los Alamos (v. fig. 29). La mancanza di una simmetria assiale in questo esperimento rende pienamente tridimensionale il problema dell'equilibrio macroscopico e praticamente impossibile fare previsioni esatte riguardo al funzionamento; l'esperimento ha poi dimostrato l'esistenza di configurazioni quiescenti, ma caratterizzate da tempi di contenimento estremamente brevi.

Un tipo diverso di configurazione ad alto β è quello toroidale a corrente distribuita e a campo invertito (reversed field pinch); in questa configurazione l'effetto del plasma sul campo toroidale è talmente forte da cambiarne il segno da un certo raggio in poi. L'instaurarsi di questa inversione può essere spontaneo o stimolato dall'esterno, ma richiede comunque il passaggio attraverso una situazione macroscopicamente instabile, superata la quale si ha una fase quiescente la cui durata nel tempo è limitata dal fatto che il campo magnetico generato dal plasma si diffonde provocando il ritorno a condizioni instabili.

Nell'esperimento Zeta, eseguito presso i laboratori di Harwell, si sono osservati già nel 1968 valori del tempo di contenimento compresi fra 3 e 10 ms e del parametro β compresi fra 10 e 40%. In seguito sono stati realizzati esperimenti di dimensioni più ridotte (HBTX I, presso i laboratori di Culham; Eta Beta I ed Eta Beta II, all'Università di Padova), per studiare meglio il fenomeno dell'inversione del campo magnetico (cosiddetta RFP).

Particolarmente promettenti sono i risultati dell'esperimento Eta Beta II, nel quale la configurazione RFP è stata realizzata con una forte riduzione dei livelli di fluttuazione dei campi magnetici, ottenendo un miglioramento del tempo di confinamento e quindi un aumento della temperatura del plasma. Sono state raggiunte temperature elettroniche di 100 eV, superando le limitazioni precedentemente imposte dall'irraggiamento prodotto dalle impurezze leggere (come l'ossigeno).

14. Fusione a confinamento inerziale

Un possibile sistema per realizzare la fusione termonucleare controllata è basato sul confinamento inerziale, che consiste nel riscaldare il combustibile termonucleare in tempi brevi rispetto a quelli che impiega per disperdersi. Questo processo è quello che si attua nella bomba H, nella quale la miscela di combustibile D-T viene riscaldata dall'esplosione di materiale fissile; quest'ultimo modo di realizzare il riscaldamento è intrinsecamente distruttivo e contaminante, per cui le ricerche si sono concentrate su altri sistemi adatti a produrre grandi densità di potenza assorbibile dal combustibile termonucleare.

Tali sistemi si possono dividere in due grandi classi: quelli che utilizzano laser e quelli che utilizzano fasci di particelle.

La fusione laser è al momento la più avanzata, per il fatto che su tale linea sono stati effettuati esperimenti con forte produzione di neutroni di origine termonucleare e quindi si è potuta studiare meglio l'interazione fascio laser-bersaglio.

Per rendersi conto dei problemi da risolvere per realizzare un reattore a fusione laser, si consideri il bilancio energetico, rappresentato in un diagramma di Basov (v. fig. 30): il laser genera un'energia E con efficienza η; se il bersaglio ha un guadagno k, al generatore di energia elettrica arriva un'energia kE, che viene convertita con efficienza α e in parte restituita al laser. Per avere una produzione netta di energia elettrica bisogna avere un guadagno k > (αη)^-1, che è dell'ordine di 100. Un obiettivo intermedio è quello di realizzare il ‛pareggio energetico' (break-even), definito da k = 1. Al fine di raggiungere tale obiettivo sono in via di sviluppo laser con potenza di 100 TW ed energia di 100 kJ per impulso.

Il miglioramento delle prestazioni della sorgente laser non è però il solo problema: bisogna anche comprendere meglio i dettagli dell'interazione del fascio con il bersaglio, per ottimizzare il progetto di quest'ultimo.

Un bersaglio per fusione laser è costituito fondamentalmente da un guscio sferico di vetro contenente il combustibile. A seconda delle dimensioni del guscio si distinguono due tipi di bersaglio: a compressione esplosiva e a compressione isoentropica o ablativa. Nel primo tipo il guscio ha un diametro di 100 μ e uno spessore di pochi μ; all'interno il combustibile è contenuto sotto forma gassosa, a una pressione che può variare da 1 a 100 atmosfere. L'impulso laser è brevissimo, da 10 a 100 ps, e causa l'esplosione del guscio, parte del quale va verso l'esterno e parte verso l'interno, dove comprime e riscalda il combustibile gassoso. In questo modo si possono raggiungere alte temperature, ma non alte compressioni del combustibile e, siccome il tasso di reazioni di fusione e quindi la potenza uscente aumentano all'aumentare della densità, il guadagno ottenibile con tale tipo di bersaglio è insufficiente per raggiungere il pareggio.

Nel secondo tipo il guscio è più spesso e viene investito da un impulso laser più lungo, per cui viene completamente ablato senza esplodere. La struttura interna è più complessa che nel primo tipo, essendo presenti un tampone di materiale pesante, ad esempio oro, per trasmettere l'impulso dall'ablatore al combustibile, e una serie di strati di combustibile, mentre il centro è vuoto.

Dato il carattere non esplosivo della compressione, va evitato l'insorgere di instabilità che distruggano la simmetria sferica: questo richiede una precisione nella concentricità dei gusci e nella lavorazione delle superfici tale da rendere necessario lo sviluppo di nuove tecnologie.

La forma dell'impulso laser in questo caso è molto importante; i suoi requisiti si possono rendere meno restrittivi con un'accurata progettazione della stratificazione del bersaglio; per questo motivo l'ottimizzazione del guadagno k richiede un grosso lavoro di simulazione numerica, che a sua volta implica la conoscenza della fisica dell'assorbimento del fascio laser, dell'ablazione, della conduzione di quantità di moto e di calore verso l'interno e della combustione termonucleare.

Per acquisire queste conoscenze vengono impiegate negli esperimenti diagnostiche raffinatissime, basate principalmente su tecniche interferometriche, per la misura della distribuzione di densità, e sull'analisi dell'emissione di raggi X e di neutroni, per la determinazione della distribuzione di temperatura.

È stato calcolato (v. Stickley, 1978) che per verificare la superiorità della compressione ablativa sono necessarie potenze di decine di terawatt, che saranno disponibili solo eccezionalmente negli esperimenti che stanno entrando ora in funzione e regolarmente invece in quelli della prossima generazione; è evidente che questa verifica costituirà una pietra miliare nell'avanzamento verso un possibile reattore a fusione con laser.

Esistono attualmente due tipi di laser che sembrano in grado di essere perfezionati fino a soddisfare i requisiti per il pareggio: uno a stato solido (Nd, neodimio, con λ = 1,06μ) e uno a gas (CO₂, anidride carbonica, con λ = 10,6μ). Questo secondo, in particolare, per il suo più alto rendimento (2 ÷ 10%), sembra l'unico utilizzabile per la produzione economica di energia elettrica. Il laser a neodimio sembra invece destinato esclusivamente a uso sperimentale; ha richiesto un grosso sviluppo tecnologico, perchè effetti non lineari nel mezzo attivo e altre cause impedivano di ottenere grandi densità di potenza. Questi effetti sono stati eliminati con un accurato filtraggio spaziale dei modi trasversali del fascio laser e con l'uso di componenti ottici ultrapuliti.

Attualmente è il laser a CO₂ che richiede uno sviluppo tecnologico: l'energia per impulso che può fornire è grande, ma la durata e la forma dell'impulso non sono ancora ben controllati; si teme inoltre che, per la sua frequenza relativamente bassa, questo tipo di laser possa eccitare microinstabilità nell'ablatore, con produzione di elettroni energetici che preriscalderebbero il combustibile impedendo una buona compressione. Come rimedio potrebbe risultare necessario operare una moltiplicazione armonica della frequenza.

Altri tipi molto promettenti di laser sono in fase di sviluppo: alcuni, come quello a KrF hanno rendimenti fino al 20%, il che implica una grossa riduzione dell'energia per impulso richiesta (a parità di potenza elettrica prodotta e di guadagno del bersaglio). Questi laser hanno lunghezze d'onda che cadono tipicamente nel vicino ultravioletto, un fatto questo molto positivo per l'accoppiamento con il bersaglio, che rende però la vita media per emissione spontanea dei livelli eccitati usati per l'azione laser molto più breve dei tempi di pompaggio che in genere si usano. Sarà quindi necessario impiegare metodi di pompaggio diversi per raggiungere le potenze necessarie affinché questi laser possano risultare utili per produrre energia da fusione nucleare.

I principali esperimenti in corso nel campo della fusione laser sono lo Shiva (Lawrence Livermore Laboratory), che impiega un laser a vetro-neodimio con potenza di 30 TW ed energia di 15 kJ per impulso, e l'Helios (laboratori di Los Alamos), basato su un laser ad anidride carbonica da 10 TW e 10 kJ.

Negli Stati Uniti sono stati proposti due laser più potenti di quelli ora menzionati: il Nova (Livermore), al vetroneodimio, con potenza di 300 TW ed energia di 300 kJ per impulso, e l'Antares (Los Alamos), ad anidride carbonica, con potenza di 200 TW ed energia per impuso di 100 kJ. Entrambi questi laser serviranno a ottenere il pareggio energetico, che è considerato la prova della fattibilità scientifica della fusione laser; il raggiungimento di questo obiettivo è condizionato dal successo dell'impiego di bersagli a compressione ablativa.

L'interesse per l'uso di fasci di particelle in luogo di laser dipende dal loro alto rendimento, dall'alta efficienza di assorbimento nel bersaglio e dal basso costo della tecnologia relativa; in particolare nell'Unione Sovietica è stata data la priorità alla fusione con fasci di particelle rispetto alla fusione laser.

L'accelerazione di fasci di particelle è concettualmente molto semplice: richiede la formazione di un impulso di alta tensione che si applica a un tubo a vuoto con due elementi, anodo e catodo, dai quali si possono estrarre rispettivamente ioni ed elettroni; un acceleratore di questo tipo, detto a diodo (v. fig. 31), può funzionare sia come acceleratore di elettroni sia come acceleratore di ioni leggeri (v. particelle elementari: Acceleratori di particelle; v. Yonas, 1979).

Sono stati risolti diversi problemi, il più importante dei quali è stato il trasporto fino al diodo di impulsi di tensione che sono dell'ordine di diversi milioni di volt; queste tensioni sono sufficienti a strappare dalla superficie del catodo elettroni che, se raggiungessero l'anodo, dissiperebbero l'energia dell'impulso; per evitare che questo succeda si isola magneticamente la linea di trasmissione. Per capire nei dettagli questo processo di isolamento è stato necessario un lungo lavoro di simulazione numerica, ma la sua natura è semplice: l'impulso stesso produce un campo magnetico che avvolge il catodo (usualmente costituito da una sbarra metallica posta tra altre due che costituiscono l'anodo) e deflette gli elettroni facendo sì che solo una piccola parte di essi riesca a raggiungere l'anodo. Alla fine della linea gli elettrodi sono conformati in modo tale che gli elettroni possano essere strappati dal catodo e raggiungere l'anodo; appena questo processo s'innesca si ha la formazione di uno strato di plasma sulle superfici di entrambi gli elettrodi, perché parte del materiale si ionizza per urto con gli elettroni; il plasma sull'anodo costituisce una fonte di ioni che vanno a neutralizzare la carica spaziale degli elettroni evitando così che si respingano a vicenda.

A valle del problema della formazione del fascio di elettroni c'è quello del suo trasporto fino al bersaglio; questo problema è stato risolto facendo propagare in aria il fascio guidato da un canale di plasma, attualmente prodotto dall'esplosione di un filamento di tungsteno e probabilmente in futuro da un impulso laser (v. fig. 32).

L'accelerazione di fasci di ioni si ottiene invertendo la polarità in un diodo del tipo appena descritto, a condizione di inibire la corrente elettronica che assorbirebbe quasi tutta l'energia disponibile; questa inibizione è realizzata impiegando un campo magnetico di intensità sufficiente a deflettere gli elettroni ma non gli ioni.

Gli ioni offrono diversi vantaggi rispetto agli elettroni: a parità di energia cinetica il cammino nel bersaglio è più breve e, siccome non sono relativistici, è possibile accumulare i fasci, cioè comprimerli in pacchetti, aumentando la potenza sul bersaglio. Il problema più importante che resta da risolvere è la focalizzazione: le aree su cui si riesce a concentrare i fasci sono ancora troppo estese.

I principali laboratori interessati alla fusione con fasci di particelle sono la Sandia di Albuquerque e l'Istituto Kurchatov di Mosca.

Nei primi e in funzione dal 1975 l'acceleratore Proto I, in grado di fornire 1 TW di potenza, attualmente impiegato per studi su fasci di ioni; nel 1977 è entrato in funzione anche Proto II, da 8 TW, destinato a fornire dati per completare il progetto del prossimo esperimento, che dovrebbe essere costituito da 36 moduli in grado di fornire una potenza totale di 60 TW; con quest'ultima macchina si prevede di avviare esperienze per l'accensione di bersagli entro il 1985.

I primi neutroni da fusione con fasci di elettroni sono stati ottenuti all'Istituto Kurchatov, dove è attualmente in funzione l'acceleratore Angara I da 1 TW e dove è in fase di costruzione Angara V da 100 TW, che dovrebbe entrare in funzione nel 1984; parallelamente vengono sviluppati bersagli ad altissimo guadagno (k > 1.000).

L'impiego di fasci di ioni pesanti è la tecnica più recente: si cerca di adattare alle esigenze della fusione gli acceleratori di alta energia sviluppati per le ricerche sulle particelle elementari; al momento attuale è allo studio la fattibilità e l'economicità di un sistema di acceleratori che fornisca le correnti necessarie per avere sul bersaglio una potenza sufficiente per accenderlo.

Un reattore a confinamento inerziale presenta il grande vantaggio, rispetto a un reattore a confinamento magnetico, che il combustibile occupa un volume piccolo e non è circondato da complessi magneti. Il problema tecnico principale è la protezione dei materiali strutturali e dell'ultimo elemento di focalizzazione del fascio, sia esso laser o particellare, dal flusso di neutroni termonucleari. Una possibile soluzione di questo problema può venire dall'impiego di un mantello di litio liquido che scorre lungo le pareti della camera di reazione; assorbendo i neutroni, il litio protegge le pareti; inoltre, essendo liquido, può fungere da trasportatore di calore, mentre le reazioni nucleari indotte in esso dai neutroni rigenerano il trizio.

15. Esperimenti di base nella fisica dei plasmi

Gli esperimenti di cui abbiamo parlato finora, benché offrano la possibilità di studiare aspetti fondamentali della fisica dei plasmi, riguardano soprattutto la realizzazione e il contenimento di plasmi ad alta temperatura, data l'importanza che questi rivestono nella ricerca sulla fusione termonucleare controllata. D'altra parte è stata costruita tutta una gamma di apparecchiature sperimentali di piccole dimensioni per studiare e isolare aspetti significativi della fisica dei plasmi, come ad esempio la propagazione di onde, la produzione di microinstabilità, la formazione di onde d'urto, le interazioni onda-particella, le proprietà di trasporto, ecc. Questi esperimenti, pur non avendo assorbito che una piccola parte degli investimenti finanziari destinati alla fisica dei plasmi e pur non essendo altrettanto famosi quanto le apparecchiature precedentemente descritte, hanno tuttavia aperto una nuova fase nella fisica dei plasmi. Infatti, sono stati proprio questi esperimenti che hanno fornito il primo accordo preciso tra predizioni teoriche e osservazioni sperimentali. Si può ricordare come fino alla prima metà degli anni sessanta la teoria dei plasmi procedesse indipendentemente dalla necessità di predire e spiegare risultati sperimentali. D'altronde gran parte degli esperimenti di vaste proporzioni fu proposta o realizzata più sulla base dell'intuizione che su solide basi teoriche, oppure come conseguenza di un indirizzo di ricerca che si era consolidato nella tradizione di certi istituti.

Come esempio possiamo citare quelle che vengono denominate ‛macchine per plasma quiescente' (spesso chiamate anche ‛macchine Q'), nelle quali viene prodotto plasma a bassa temperatura in mezzo a due dischi caldi di tungsteno, mediante un processo di ionizzazione per contatto di un fascio di plasma di cesio o di potassio. La colonna di plasma e le linee del campo magnetico sono dritte (v. fig. 33) e di conseguenza alle estremità il plasma non è confinato; il rifornimento di ioni ha luogo per ionizzazione e quello degli elettroni attraverso l'emissione dai dischi terminali. Si può dimostrare che questa emissione di elettroni permette anche di sopprimere le instabilità di scambio discusse nel cap. 3. Nella colonna di plasma si possono allora verificare microinstabilità cosiddette ‛universali' o ‛di deriva', caratterizzate da fluttuazioni della densità e del campo elettrico che si accrescono a spese dell'energia termica degli elettroni nella direzione del campo magnetico.

Se il cammino libero medio collisionale degli elettroni è più breve della lunghezza della colonna del plasma, questo processo di trasferimento di energia può manifestarsi a causa del valore finito della resistività elettrica dello stesso plasma e della sua conducibilità termica lungo le linee del campo magnetico. Come si è visto nel cap. 2, in questo caso infatti il moto delle particelle può risultare disaccoppiato da quello delle linee del campo magnetico. Si può inoltre dimostrare che gli urti ione-ione (v. Coppi e altri, 1967), che danno il contributo principale alla viscosità nella direzione trasversa rispetto alle linee del campo magoetico, tendono a smorzare i modi di deriva. Inoltre questa viscosità trasversale è proporzionale al quadrato del raggio di rivoluzione degli ioni, di modo che è possibile variarla tenendo fissa la temperatura del plasma e variando il campo magnetico. Ne segue, come è indicato nella fig. 34, che è possibile controllare la produzione dei vari modi di oscillazione e, studiando il loro insorgere, paragonare le osservazioni sperimentali con i risultati della teoria linearizzata di cui si è parlato nel cap. 3.

16. Realizzabilità scientifica della fusione termonucleare controllata

Indicheremo brevemente i principali traguardi che bisogna raggiungere per dimostrare la realizzabilità scientifica di un reattore termonucleare.

Il primo è rappresentato dalla cosiddetta temperatura di accensione ideale o temperatura critica, alla quale l'energia generata nel plasma attraverso il processo di fusione pareggia le perdite di energia per radiazione di Bremsstrahlung causate dalle collisioni a breve distanza tra elettroni e nuclei. A titolo illustrativo, nella tab. III sono riportate le temperature critiche per due importanti reazioni di fusione. Un altro requisito è dato dal prodotto del tempo di confinamento dell'energia per la densità: esso deve essere sufficientemente grande da indurre una produzione netta di energia. Questo corrisponde al cosiddetto criterio di Lawson, che si deriva dalla fisica dei processi di fusione, combinato con alcune valutazioni dell'efficienza dei processi di recupero dell'energia in un ipotetico reattore a fusione.

Questi fatti sono descritti nella fig. 35. È evidente che la reazione deuterio-trizio (D-T) è la più facile da ottenere a causa della sua bassa temperatura di innesco.

(I capitoli 7, 8, 11, 13 e 14 sono stati scritti in collaborazione con il dr. Paolo Buratti della Scuola Normale Superiore di Pisa).

bibliografia

Alfvén, H., Cosmical electrodynamics, London 1950.

Artsimovich, L.A., Tokamak devices, in ‟Nuclear fusion", 1972, XII, pp. 215-252.

Bickerton, R. J., The Tokamarks TFTR, JT-60 and JET, in Physics of plasma close to thermonuclear conditions, Varenna 1979.

Boxman, G. J. e altri, Low and high density operation of Alcator, in Controlled fusion and plasma physics, Lausanne 1975, vol. II, p. 14.

Brueckner, K. A., Jorna, S., K.M.S. Fusion Inc., Reort KMSF-U97, Ann Arbor 1973.

Callen, J., Coppi, B., Dagazian, R., Gajewski, R., Sigmar, D., Collective modes in high-current-carrying confined plasmas, in Plasma physics and controlled thermonuclear research 1971, International Atomic Energy Agency, Wien 1971, vol. II, pp. 451-477.

Chandrasekhar, S., Hydrodynamic and hydromagnetic stability, Oxford 1961.

Chen, F. F., The leakage problem in fusion reactors, in ‟Scientific American", 1967, CCXVII, pp. 76-88.

Coppi, B., Hendel, H. W., Perkins, F., Politzer, P. A., Interpretation of experiments on collisional drift modes, in Proceedings of the symposium on quiescent plasmas, CNEN, Frascati 1967, pp. 201-211.

Coppi, B., Mazzucato, E., Anomalous plasma resistivity at low electric fields, in ‟Physics of fluids", 1971, XIV, pp. 134-149.

Coppi, B., Rem, J., THe tokamk approach in fusion research, in ‟Scientific American", 1972, CCXXVII, pp. 65-75.

Coppi, B., ROsenbluth, M. H., Collisional interchange instabilities in shear and ζdl/B stabilized systems, in Plasma physics and controlled thermonuclear research, International Atomic Energy Agency, Wien 1966, vol. I, pp. 617-641.

Cowling, T. G., Magnetohydrodynamics, New York 1957.

Fowler, T. K., Post, R. F., Progress toward fusion power, in ‟Scientific American", 1966, CCXV, pp. 21-31.

Galeev, A. A., Sagdeev, R. Z., Transport phenomena in a collisionless plasma in a toroidal magnetic system, in ‟Soviet physics: JETP", 1968, XXVI (1967), pp. 233-240.

??? Hearings on controlled thermonuclear research, Joint Committee on Atomic Energy, U.S. Government printing office, vol. I, Washington 1972.

Hirsch, R. L., Laser and relativistic beam research program, in Hearings on controlled thermonuclear reserach, Washinton 1972, part 1, pp. 109-115.

Langmuir, I., The interactoin of electron and positive ion space charges in cathode sheaths, in ‟Physical review", 1939, XXXIII, pp. 954-990.

Leontovich, M. A., reviews of plasma physics, voll. I-V, New York 1965-1971.

Lin, C. C., Stellar dynamical theory of normal spirals, in Lectures in applied mathematics, New York 1967, vol. IX, pp. 66-97.

Montgomery, D. C., Tidman, D. A., Plasma kinetic theory, New York 1964.

Nuckolls, J., Emmet, J., Wood, L., Laser-induced thermonuclear fusion, in ‟Physics today", 1973, XXVI, 8, pp. 46-53.

Ohkawa, T., Fusion research at Gulf General Atomics, in Hearings on controlled thermonuclear research, Washington 1972, part 1, pp. 124-133.

Petschek, M. E., Magnetic field annihilation, in Symposium on the physics of solar flares, NASA, Washington 1963, pp. 425-439.

Piddington, J. H., Cosmic electrodynamics, New York 1969.

Ribe, F. L., The Los lamos theta-pinch program, in Hearings on controlled thermonuclear research, Washington 1972, part 1, pp. 94-108.

Schmidt, G., Physics of high temperature plasmas, New York 1966.

Simon, A., Thompson, W. B., Advances in plasma physics, voll. I-IV, New York 1968-1972.

Spitzer, L. Jr., Physics of fully ionized gases, New York 1962.

Stickley, C. M., Laser fusion, in ‟Physics today", 1978, XXXI, 5, pp. 50-58.

Yonas, G., Energia da fusione con fasci di particelle, in ‟Le scienze", 1979, CXX, pp. 11-23.

Plasmi in astrofisica di Yaguri B. Zeldovich

sommario: 1. Problemi astrofisici legati ai plasmi. a) Le stelle e il Sole in particolare. b) La corona solare. c) I relitti delle supernove. d) Il gas interstellare. e) L'Universo primordiale. 2. Classificazione dei plasmi in astrofisica. a) Plasmi caldi in equilibrio termico. b) Plasmi diluiti a bassa temperatura. c) Plasmi degeneri: materia fredda e densa. d) Plasmi degeneri relativistici. e)Plasmi relativistici in equilibrio ad alta temperatura. f) Plasmi otticamente sottili. g) Plasmi magnetizzati otticamente sottili. 3. Proprietà dei plasmi importanti per l'astrofisica. a) Opacità di un plasma in equilibrio. b) Conducibilità elettrica. c) Campi magnetici nei plasmi. d) La condizione di neutralità elettrica. e) Oscillazioni del plasma. f) Plasmi dominati dalla radiazione. □ Bibliografia.

1. Problemi astrofisici legati ai plasmi

Quasi tutti i corpi celesti, stelle, pulsar, galassie, quasar - come pure la materia rarefatta che li separa, vale a dire il gas interstellare e il gas intergalattico -, possono essere classificati come plasmi di vario tipo, con l'unica eccezione dei pianeti che si sono solidificati raffreddandosi. Per plasma si intende uno stato della materia in cui il grado di ionizzazione sia abbastanza elevato da far si che le interazioni elettromagnetiche tra le particelle cariche siano determinanti per la dinamica del sistema (v. sopra, plasmi in fisica). Secondo le moderne vedute cosmologiche, la struttura dell'Universo che noi oggi osserviamo, cioè le galassie, i quasar, gli ammassi, non è altro che il risultato di un'evoluzione, dal momento che si ritiene che in tempi remoti non vi fosse altro che un plasma caldo e uniformemente distribuito.

Dopo queste considerazioni ben si comprende l'importanza che la teoria dei plasmi assume in vari campi dell'astronomia e dell'astrofisica. In questo articolo passeremo in rassegna le caratteristiche specifiche dei plasmi che formano i corpi celesti e la materia rarefatta.

a) Le stelle e il Sole in particolare

Il Sole consiste di una miscela di gas composta per il 70% all'incirca da idrogeno, per il 28% da elio e per il 2o% da elementi più pesanti. La densità media del Sole è di circa i g/cm³ (con densità di 100 g/cm³ al centro), mentre la temperatura varia da 15.000.000 °K al centro a circa 5.760 °K alla superficie. In queste condizioni tutti gli atomi sono completamente ionizzati nelle zone interne del Sole, dove si ha quindi un plasma totalmente ionizzato. La regione centrale, che comprende circa il 10% della massa totale, è anche la zona in cui hanno luogo le reazioni nucleari che trasformano l'idrogeno in elio e che sono la sorgente dell'energia che il Sole irradia nello spazio circostante.

Alla superficie, dove si forma la radiazione che noi osserviamo direttamente, l'elio è invece allo stato neutro, mentre l'idrogeno e altri elementi sono parzialmente ionizzati, per cui si può ancora parlare di plasma. È proprio la presenza di atomi neutri e di ioni con parte degli elettroni ancora legati che determina le caratteristiche spettrali della radiazione solare.

Gli strati compresi tra il nucleo centrale, dove avvengono le reazioni nucleari, e la superficie, da cui viene emessa la radiazione, si trovano in condizioni fisiche intermedie. La luminosità del Sole è determinata dal processo di diffusione dell'energia attraverso questi strati.

La situazione nelle altre stelle di tipo normale è simile a quella del Sole: non vi sono cioè parti della stella in cui tutti gli elettroni sono legati ai nuclei, ciò che impedirebbe di considerare la materia allo stato di plasma. La differenza rispetto al Sole è soltanto quantitativa. Nelle stelle giganti la temperatura centrale raggiunge 1,5-2,0 × 10⁶ °K, mentre la densità è dell'ordine di 10⁴ g/cm³. In queste condizioni diviene possibile la combustione nucleare dell'elio in carbonio, un processo più difficile a realizzarsi che non la combustione dell'idrogeno. La temperatura superficiale di queste stelle si abbassa a 2.000-3.000 °K di modo che il grado di ionizzazione è piuttosto basso.

b) La corona solare

Osservazioni astronomiche del Sole effettuate durante le eclissi totali avevano rivelato già in passato la presenza di una certa quantità di gas luminoso che circonda il Sole estendendosi fino a qualche milione di chilometri, cioè a una distanza maggiore del raggio solare. Studi moderni hanno provato l'esistenza di un flusso di plasma proveniente dal Sole, il cosiddetto vento solare. Si tratta di un plasma rarefatto ad altissima temperatura (circa 2 × 10⁶ °K), la cui fonte di energia è certamente il Sole stesso. D'altronde bisogna notare che la parte più importante dell'energia emessa dal Sole, cioè la radiazione a una temperatura di circa 5.760 °K, non può certo riscaldare la corona fino a temperature di milioni di gradi. Questo riscaldamento è invece causato da sorgenti di energia assai più modeste, onde acustiche per esempio, che però permettono di raggiungere temperature altissime. A causa della sua bassa densità, la corona irradia debolmente, meno dello 0,0001% dell'emissione totale del Sole: essa rimane però la sorgente predominante della radiazione solare, nella gamma delle radioonde e in quella della radiazione penetrante (raggi X, protoni, elettroni), che può mettere in pericolo la vita degli equipaggi dei veicoli spaziali. Il flusso di plasma caldo che inizialmente forma la corona raggiunge la Terra e interagisce con il campo magnetico e con la ionosfera dando luogo a importanti fenomeni, come le tempeste magnetiche e le aurore polari.

c) I relitti delle supernove

Gli astronomi antichi e medievali ci hanno tramandato descrizioni del fenomeno delle stelle supernove. Si tratta di un processo di eccezionale violenza che si manifesta con l'apparizione inaspettata di una nuova stella. In alcuni casi la nuova stella risulta così brillante da poter esser vista anche di giorno, ma dopo un tempo breve, di qualche mese, si affievolisce e scompare.

Nella posizione in cui appare una supernova si osserva, per qualche migliaio di anni, la radiazione luminosa emessa da un particolare tipo di nebulosa. Moderni studi (Gordon, Ship, Shklovskij) hanno rivelato che tale radiazione viene emessa da elettroni relativistici (cioè dotati di velocità assai prossime a quella della luce) che si muovono su traiettorie a forma di spirale in un campo magnetico. Anche altri corpi celesti emettono questo tipo di radiazione, detta di sincrotrone dal nome dell'acceleratore di particelle in cui essa può essere facilmente osservata. L'analisi della radiazione emessa dai quasar permette di considerare plausibile l'ipotesi che anche tali oggetti emettano radiazione di sincrotrone. Questi casi sono altrettanti esempi di plasmi rarefatti, relativistici e magnetizzati.

d) Il gas interstellare

Lo spazio che separa una stella dall'altra nella nostra galassia non è vuoto. In media esso contiene un elettrone e un protone ogni 10 centimetri cubici, alla temperatura, relativamente modesta, di 10.000 °K.

La radiazione emessa da questo plasma rarefatto è assai debole. Si è avuta prova della sua esistenza recentemente, attraverso lo studio della propagazione delle onde radio provenienti dalle pulsar. La velocità di propagazione delle radioonde in un plasma è infatti leggermente minore di quella della luce nel vuoto e dipende in modo caratteristico dalla frequenza. I singoli impulsi emessi dalle pulsar coprono uno spettro di frequenze piuttosto largo e hanno una durata compresa tra 10^-3 e 10^-1 secondi. Il tempo totale del tragitto è dell'ordine di qualche migliaio di anni, ma per le onde radio è di 10-100 secondi maggiore che non per la luce. Questa differenza è facilmente misurabile e fornisce indirettamente il valore della densità elettronica lungo il cammino.

Una parte del gas interstellare è concentrata in nubi, più dense e più fredde del gas circostante (di densità dell'ordine di 10 o 100 atomi/cm³ e temperatura di circa 100 °K). Queste nubi sono debolmente ionizzate per effetto della radiazione cosmica e dei raggi X: se tale materia fredda e oscura possa ancora essere considerata un plasma è solo una questione di terminologia.

e) L'Universo primordiale

Secondo le moderne teorie cosmologiche, l'Universo deve avere subito un'evoluzione. Nello stato iniziale la temperatura doveva raggiungere valori elevatissimi e la materia doveva essere dispersa uniformemente con una densità enormemente maggiore di quella attuale. A causa dei valori estremi della temperatura, la densità della radiazione doveva superare quella della materia. Un tale stato, in cui la materia è stemperata in un campo di radiazione, si chiama ‛plasma dominato dalla radiazione'. A partire da questo stato iniziale l'Universo si sarebbe evoluto, espandendosi. La cosmologia che si basa su questo modello è nota comunemente come cosmologia del 'big-bang', ossia della grande esplosione.

In stadi successivi la materia si sarebbe gradualmente andata aggregando fino a formare galassie e stelle, mentre la radiazione primordiale sarebbe tuttora distribuita uniformemente. La presenza di questa ‛radiazione cosmica residua' (o background radiation) è stata rivelata e il suo spettro coincide con quello di un corpo nero alla temperatura di 2,7-3 °K.

Secondo le teorie cosmologiche, nei primi secondi dopo l'esplosione, il plasma doveva consistere di una miscela di tutti i tipi di particelle e antiparticelle, oltre che, naturalmente, di radiazione. L'abbassamento della temperatura e l'annichilazione di particelle e antiparticelle che accompagnarono l'espansione avrebbero contribuito a formare successivamente un plasma cosmico, composto di radiazione (fotoni, neutrini e antineutrini) e di una piccola quantità di materia ordinaria (protoni, elettroni, nuclei di elio). In questo stadio la forte interazione tra radiazione e materia avrebbe impedito la condensazione di quest'ultima in entità separate, cioè in galassie e stelle. Lo stadio successivo avrebbe avuto inizio dopo circa 100.000 anni, cioè quando protoni ed elettroni si sarebbero legati per formare atomi neutri. Da quel momento si sarebbero potute formare le galassie, con la materia non più in stato di plasma.

Quanto abbiamo detto non pretende certamente di essere un resoconto dettagliato delle nostre conoscenze sui vari oggetti che sono stati ricordati, stelle; Universo primordiale ecc., ma vuole indicare soltanto brevemente la presenza di plasmi nei vari sistemi, mettendo in rilievo le differenti condizioni fisiche in cui si può presentare il plasma nell'Universo, sia ai giorni nostri, che nel lontano passato.

2. Classificazione dei plasmi in astrofisica

Come abbiamo visto, i plasmi si possono presentare in situazioni e condizioni molto diverse. Le condizioni fisiche prevalenti nei diversi tipi di plasma permettono di classificarli nel modo seguente.

a) Plasmi caldi in equilibrio termico

Consideriamo una certa quantità di plasma, cioè di elettroni e ioni, confinata in un dato volume e mantenuta a una data temperatura. In un tale plasma hanno luogo processi di vario tipo: collisioni tra due elettroni, con conseguente variazione delle velocità, e collisioni tra elettroni e ioni, con eventuale emissione di radiazione elettromagnetica (cioè creazione di fotoni). La radiazione può anche essere assorbita (cioè i fotoni possono essere distrutti) nelle collisioni elettroniche oppure può venire diffusa.

Nonostante la complessità di tutti questi processi è piuttosto semplice predire quale sarà lo stato finale del sistema. Se i fotoni, come gli elettroni e gli ioni, sono confinati nel volume considerato, si raggiungerà uno stato di equilibrio termodinamico. In tale stato tutti i processi che sono stati enumerati seguitano ad aver luogo, ma si bilanciano reciprocamente: per esempio, l'emissione di radiazione viene esattamente compensata dall'assorbimento. Questo avviene con una densità di energia e uno spettro della radiazione che hanno un valore e una forma ben definiti. La densità numerica di fotoni (cioè il numero di tali particelle per centimetro cubo) all'equilibrio, è data da n_f ≃ 20 T³, dove T è la temperatura assoluta. L'energia media di un fotone è hν ≃ 3kT (dove k 1,38 × 10^-16 erg/°K è la costante di Boltzmann), cosicché la densità d'energia diviene ε_r ≃ 8 × 10^-15T⁴ erg/cm³. Quest'ultima è da confrontare con la densità d'energia, ε, legata al moto termico degli elettroni e dei nuclei. Per un plasma completamente ionizzato è ε = 3/2 nkT, dove n, densità numerica di particelle, è legata alla densità di materia ρ_m dalla relazione

in cui Z è il numero atomico e A il peso atomico.

I plasmi in equilibrio termodinamico si possono quindi dividere in due classi: quelli in cui sono dominanti la densità d'energia dovuta alla materia e la densità numerica delle particelle (ciò che avviene per T ⟨ T₁, con T₁ = 1,5 × 10⁷ ρm^1/3) e quelli in cui sono invece dominanti la densità di energia della radiazione e la densità numerica dei fotoni (T > T₁). Nella figura è riportato un diagramma illustrativo dei domini di definizione dei vari tipi di plasma.

Il confronto fra la densità di massa della radiazione, = ρ_r = ε_r/c² = 8,7 × 10^-35 T⁴, e la densità di massa della materia, ρ_m, definisce un altro confine nella figura, cioè T₂ = 5,9 × 10⁸ ρm^1/4. Per T > T₂ la densità di materia è maggiore di quella di radiazione, mentre per T > Τ₂ è vero l'opposto e siamo in presenza di un plasma dominato dalla radiazione.

b) Plasmi diluiti a bassa temperatura

Nella regione di temperature molto basse (e basse densità) troviamo la materia ordinaria, cioè nuclei con elettroni fortemente legati: non si hanno plasmi di alcun tipo. La temperatura T₃ a cui la ionizzazione comincia a farsi sensibile è dell'ordine di 5.000-10.000 °K per la maggior parte degli atomi e delle molecole. Un'importante eccezione a questa regola è costituita dai vapori dei metalli alcalini, sodio, potassio, rubidio e cesio, che hanno elettroni debolmente legati. Per tali sostanze T₃ è dell'ordine di 2.000 °K, ma la loro abbondanza in natura è scarsa e tale è anche la loro importanza in astrofisica.

La formula approssimata che dà la densità elettronica, n_e, in un plasma a bassa temperatura è

n_e = 7 × 10¹⁰ √-n-_a 10^-2.520J/T

dove n_a è la densità (numerica) degli atomi e J l'energia di ionizzazione espressa in elettronvolt (pari a 13,6 eV per l'idrogeno, a 5,4 eV per il sodio, ecc.).

c) Plasmi degeneri: materia fredda e densa

Una densità molto grande può, almeno in parte, avere lo stesso effetto di un'elevata temperatura, può cioè indebolire il legame tra nuclei ed elettroni e trasformare la materia ordinaria in plasma.

Nelle condizioni ordinarie di temperatura, pressione e alte densità (comprese tra 0,5 e 20 g/cm³), caratteristiche dei normali solidi e liquidi, parte delle sostanze sono dielettriche o semiconduttrici e parte metalliche. Se i metalli possano essere chiamati plasmi o no, è ancora una volta una questione di terminologia; quel che è certo è che i metalli conducono l'elettricità e che, quindi, almeno parte dei loro elettroni sono in grado di muoversi liberamente al loro interno: si può quindi parlare di effetti di plasma nei metalli. Aumentando notevolmente la pressione esterna (oltre cento milioni di atmosfere = 10¹⁴ dine/cm²), fino a comprimere la materia in volumi parecchie volte più piccoli di quelli che occupa normalmente, si trova che tutte le sostanze presentano caratteristiche metalliche, le differenze chimiche tra le varie sostanze scompaiono e il comportamento della materia è governato dal principio di Pauli, secondo il quale, applicato agli elettroni, ‛due elettroni non possono mai trovarsi nello stesso stato'. Pertanto, se si cerca di confinare un gran numero di elettroni in un piccolo volume, essi devono via via occupare livelli energetici sempre più alti e quindi, anche per temperature vicine allo zero assoluto, la loro energia cinetica e la loro pressione raggiungono valori notevoli. Le stelle nane, per esempio, prive di sorgenti di energia nucleare, sono sostenute dalla pressione dovuta allo stato di degenerazione degli elettroni a bassissima temperatura. In un tale stato degenere la pressione è data approssimativamente da p = 3 × 10¹²ρm^5/3, con p in dine/cm² e ρ_m in g/cm³, ed è indipendente dalla temperatura.

Grande contributo allo studio della fisica del gas degenere di elettroni fu dato da E. Fermi, che elaborò la teoria dei metalli considerandoli sistemi di elettroni degeneri; il massimo livello energetico occupato da questi elettroni viene detto ‛livello di Fermi' e la corrispondente energia ‛energia di Fermi', ecc. Gli elettroni sono un esempio particolare di ‛fermioni', come i protoni, i neutroni, i muoni, ecc.

Una proprietà assai importante degli elettroni degeneri è quella di non emettere radiazione, sebbene possano collidere anche ad energia elevata con i nuclei. Per emettere radiazione, come è noto, un elettrone deve passare a uno stato di energia inferiore; questa transizione però è proibita dal principio di Pauli, essendo il secondo stato energetico già occupato da altri elettroni.

Lo stato rimane degenere fin quando l'energia kT associata al moto termico non supera l'energia di Fermi degli elettroni. Ciò fornisce un nuovo limite di temperatura, T₄: per T ⟨ T₄ il plasma è degenere, per T > T₄ si ha un normale plasma caldo (v. § a). La formula approssimata per T₄, valida per 10² ⟨ ρ_m ⟨ 8 × 10⁶ g/cm³, è data da T₄ = 8 × 10⁴ ρm^2/3. Anche questo limite è riportato nella figura.

d) Plasmi degeneri relativistici

A densità ρ_m > ρ₁ = 2 × 10⁶ g/cm³ l'energia di Fermi degli elettroni degeneri è maggiore dell'energia di riposo m_ec² (con m_e ≃ 9 × 10^-28 g massa elettronica). In pratica ciò significa che a tali densità, anche a bassissime temperature, gli elettroni si muovono con velocità vicina a quella della luce e si dicono quindi elettroni ‛relativistici'. Quando la loro energia raggiunge il valore critico di circa 40 m_ec² = 20 MeV, essi incominciano a interagire con i nuclei, trasformando i protoni in neutroni. Di conseguenza a densità maggiori di ρ₂ ≃ 10¹² g/cm³ il plasma degenere si trasforma in un liquido composto di neutroni. Si ritiene che le pulsar consistano, almeno in parte, di un tale liquido neutronico. Soltanto gli strati esterni di una pulsar (dove pressione e densità sono minori che all'interno) sono formati invece da un plasma relativistico con elettroni degeneri e nuclei nello stato ordinario.

e) Plasmi relativistici in equilibrio ad alta temperatura

Anche a basse densità è possibile avere elettroni di alta energia, per effetto di temperature elevate. Energie dell'ordine dell'energia di riposo degli elettroni (m_ec² ≃ 8 × 10^-7 erg) corrispondono a una temperatura T₅ = 6 × 10⁹ °K. In condizioni di equilibrio si ha, corrispondentemente, una densità di radiazione (cioè di fotoni) ρ_r = 8 × 10^-36 T⁴, che, per T > T₅, dà ρ_r > 10⁴ g/cm⁵. L'aspetto nuovo di un plasma relativistico in equilibrio termico è dato da un'abbondante produzione di particelle e antiparticelle. Quando T > T₅, per esempio, si producono coppie di elettroni e positoni e le rispettive concentrazioni di equilibrio sono dello stesso ordine di grandezza della densità fotonica, in modo che la densità totale risulta triplicata, ρ_e±,γ = 3ρ_r. In linea di principio coppie di elettroni e positoni sono presenti anche a temperatura minore, ma solo in piccola quantità (proporzionale a 10^{-0,43 T5/T}, cioè a e^-T5/T). Inoltre si ha anche una certa produzione di neutrini e antineutrini principalmente per effetto della reazione e⁺ + e^- → ν + ν̄. In astrofisica i processi nei quali si ha produzione di neutrini danno origine alle due seguenti situazioni caratteristiche.

1. I neutrini possono uscire con grande facilità dalla regione centrale di una stella. Una tale regione può venire dunque trattata come un plasma in equilibrio solo con riferimento alle particelle e ai fotoni, ma non ai neutrini e agli antineutrini. La produzione di questi e il loro successivo deflusso rappresentano in realtà un meccanismo che comporta una perdita di energia e quindi provoca un raffreddamento del plasma.

2. Su scala cosmologica, in un Universo senza confini, permeato di plasma, non si ha perdita di neutrini. Quei neutrini che nascono in un certo volume e che successivamente ne escono vengono completamente rimpiazzati dai neutrini che fluiscono nella stessa regione dallo spazio circostante. Di conseguenza in cosmologia si ammette l'esistenza di un plasma in completo equilibrio, nel quale sono compresi anche i neutrini. Ciò aumenta ancora la densità totale, per ogni data temperatura, di un fattore pari a circa 1,5 o 2.

Una conclusione importante che deriva da quanto si è detto è che attualmente l'Universo è permeato non solo dalla radiazione elettromagnetica residua a 2,7 °K, ma anche da una radiazione di fondo neutrinica a 2 °K. La piccola differenza tra le due temperature per i due tipi di radiazione è dovuta a sottili effetti che si manifestano durante l'annichilazione di e⁺ ed e⁻.

La verifica sperimentale della prevista esistenza di una radiazione di fondo neutrinica (corrispondente a 200 particelle per cm³ e a un'energia di 10^-3 eV/cm³) è molto importante, ma altrettanto difficile, e finora non è stata tentata. (Un tempo si riteneva che la massa di riposo del neutrino fosse esattamente eguale a zero. Oggi si stanno eseguendo misure sperimentali al riguardo. Una massa di riposo anche minima, di soli 10 ÷ 30 eV, muterebbe grandemente la nostra concezione cosmologica).

f) Plasmi otticamente sottili

La densità del plasma nella corona solare, nella nebulosa del Granchio e nello spazio interstellare della nostra galassia è molto bassa, essendo compresa tra 10^-1 e 10⁶ elettroni/cm³. Un plasma così diluito è trasparente alla radiazione visibile e in genere a qualunque tipo di radiazione, eccezion fatta per le radioonde di maggior lunghezza d'onda. In questi casi non esiste una situazione di equilibrio: la radiazione emessa nei processi di collisione fra elettroni e nuclei può uscire liberamente dal plasma, poiché la probabilità che venga assorbita o diffusa è minima. In ogni istante la densità di radiazione è trascurabile rispetto a quella che si avrebbe in condizioni di equilibrio. Anche nel caso che la densità ρ e la temperatura T del plasma corrispondano a uno stato della regione in cui domina nettamente la radiazione (v. fig.), in un plasma otticamente sottile questa può liberamente uscire dal plasma senza esser così più in grado di raggiungere una densità dominante rispetto a quella della materia. Questo è possibile quando si pensi che per un plasma la proprietà di essere otticamente sottile non dipende solo dai valori di ρ e T, ma anche dalla dimensione lineare, R, caratteristica del volume occupato.

La probabilità che la diffusione della radiazione sia piccola è espressa dalla condizione ρ_mR > 3g/cm² (per l'idrogeno completamente ionizzato). Per esempio, se consideriamo il gas interstellare di densità ρ_m ≃ 10^-24 g/cm³, distribuito su un volume di dimensione lineare R = 10 chiloparsec = 3 × 10²² cm, pari al raggio della Galassia, otteniamo ρR ≃ 3 × 10^-2 g/cm², che è un valore cento volte minore di quello critico.

La condizione che esprime invece una probabilità piccola di assorbimento della luce è più complicata, poiché dipende dalla frequenza della radiazione e dalla temperatura, oltre che dalla densità e dalle dimensioni. Essa, comunque, risulta soddisfatta nel caso degli oggetti celesti menzionati.

Che la corona solare sia trasparente è un fatto ovvio: in caso contrario la sua brillanza sarebbe confrontabile con quella del disco centrale.

Da quanto detto segue l'importanza dei plasmi otticamente sottili in astrofisica. La loro proprietà più importante è la continua emissione di radiazione, che nel caso più semplice ha luogo durante le collisioni degli elettroni con i nuclei. I fotoni emessi hanno un'energia media paragonabile a quella degli elettroni. L'intensità della radiazione, in erg cm^-3 s^-1, è data da W = 10^-27 n_en_nZ²T^1/2, dove n_e è la concentrazione elettronica, n_n quella dei nuclei, Z la carica dei nuclei e T la temperatura assoluta. La perdita di energia è dunque proporzionale al quadrato della densità. Un plasma rarefatto irradia perciò assai debolmente e il tempo necessario perché si raffreddi è grande anche su scala astronomica. In un plasma più denso il tempo di raffreddamento è corrispondentemente minore, così che un plasma denso e sottile può sopravvivere a lungo solo se è alimentato da una qualche sorgente di energia. Il tempo di raffreddamento, espresso in anni, è τ ≃ 10⁴ T^1/2/n. Per il gas interstellare (n = 0,1 e T = 10⁴ °K) si ottiene τ = 10⁷ anni. Il tempo di raffreddamento caratteristico della corona solare è invece molto minore.

A temperature basse, minori di 10⁵ °K, lo spettro di emissione è costituito prevalentemente di righe, nella regione del visibile e dell'ultravioletto, così che si può far uso dell'analisi spettrale per determinare la composizione e la temperatura del plasma; a temperature molto elevate hanno luogo altri processi. La produzione di coppie particella-antiparticella in un plasma otticamente sottile è fortemente limitata dalla scarsità di fotoni presenti. In un plasma otticamente sottile i positoni cominciano a essere relativamente abbondanti solo a temperature dell'ordine di 10¹¹ °K, in confronto ai 5 × 10⁹ °K necessari per un plasma in equilibrio. Plasmi di interesse astrofisico otticamente sottili con una certa concentrazione di positoni non sono ancora stati scoperti.

g) Plasmi magnetizzati otticamente sottili

Assai spesso, in situazioni di interesse astrofisico, il plasma è permeato da un campo magnetico, il quale fa sì che le traiettorie delle particelle siano a forma di spirali, risultanti dalla sovrapposizione di un moto rettilineo lungo le linee del campo e di un moto rotatorio intorno ad esse. In assenza di campo magnetico le particelle del plasma sfuggirebbero rapidamente dal volume originariamente occupato; il campo, invece, limita la perdita di particelle e rende stabile la configurazione del plasma. Il ruolo dei campi magnetici è particolarmente importante proprio per i plasmi rarefatti e otticamente sottili.

Il moto circolare degli elettroni in un campo magnetico è accompagnato dall'emissione di radioonde, la cosiddetta ‛radiazione di sincrotrone'. Per elettroni non relativistici la frequenza ν della radiazione è uguale alla frequenza di girazione ed è dell'ordine di 3 × 10⁶ Hz. Gli elettroni relativistici emettono a lunghezze d'onda minori, cioè a frequenze più elevate: la loro emissione è massima alla frequenza

ν_m = 4,6 × 10⁶ HE²,

dove E è l'energia degli elettroni, espressa in MeV, H è l'intensità del campo magnetico, espressa in gauss, e ν è la frequenza, espressa in hertz.

Nel caso delle pulsar si è avanzata l'ipotesi che il campo H sia così intenso e gli elettroni così energetici da produrre, mediante il meccanismo di sincrotrone, anche luce visibile (ν = 10¹⁵ Hz) e raggi X (ν compresa tra 10¹⁹ e 10²⁰ Hz). Il valore del campo magnetico, dell'ordine di 10¹² gauss, si ricava dall' osservazione delle righe dello spettro X di una pulsar.

Gli elettroni relativistici, in presenza dì radiazione di bassa frequenza, possono perdere la loro energia interagendo con i fotoni. Il processo fisico attraverso cui si realizza questo effetto è la diffusione di fotoni da parte di elettroni: esso fu previsto per primo da Thomson e studiato poi da Compton per mezzo di raggi X. Quando si hanno raggi X ed elettroni lenti, come nella materia ordinaria, il fotone cede una parte della propria energia all'elettrone. Invece, nel caso di una collisione frontale di un elettrone relativistico con un fotone, si ha un trasferimento di parte dell'energia dell'elettrone al fotone diffuso; questo processo viene indicato col nome di effetto Compton inverso. La frequenza v₁ dei fotoni dopo la diffusione e la frequenza ν₀ prima della diffusione sono legate dalla relazione

ν₁ = ν₀ (E/m_ec²)²,

dove E è l'energia dell'elettrone. Gli elettroni relativistici, interagendo con fotoni radio o infrarossi, producono con questo meccanismo luce visibile e anche raggi X.

Nei plasmi molto rarefatti (mezzo interstellare nella Galassia e mezzo intergalattico) le interazioni degli elettroni relativistici con i fotoni hanno un'importanza maggiore che non quelle degli elettroni con i nuclei. A causa delle perdite di energia, gli elettroni più energetici, con E > 10⁹ m_ec², vengono rapidamente eliminati dai raggi cosmici. Vogliamo far notare qui che la radioemissione delle pulsar, quando si tenga conto delle piccole dimensioni della regione emittente, è sicuramente troppo forte per essere attribuita al moto di singoli elettroni in un campo magnetico. Questo punto verrà ripreso nel prossimo capitolo.

3. Proprietà dei plasmi importanti per l'astrofisica

a) Opacità di un plasma in equilibrio

Nella fisica solare e stellare l'opacità del plasma è una delle proprietà più importanti. La quantità di energia che una stella irradia nell'unità di tempo dipende dall'opacità e in minor misura dalle proprietà nucleari, in quanto la generazione di energia dovuta alle reazioni nucleari si regola in modo da compensare le perdite energetiche dovute all'opacità. Questa è causata dalla diffusione di fotoni: la concentrazione di fotoni di qualsiasi frequenza è maggiore là dove la temperatura è maggiore e quindi la propagazione casuale dei fotoni in tutte le direzioni porta a un flusso medio di energia dalle regioni di temperatura alta verso quelle di temperatura più bassa. Il flusso di energia per unità di tempo e per unità di area, tra due superfici a temperature T₁ e T₂ e distanti x₁ − x₂, è dato da

dove T = ½(T₁ + T₂) è la temperatura media. Il coefficiente numerico dipende dalla composizione del plasma ed è stato calcolato nel caso del Sole.

Il cammino che i fotoni percorrono dipende dal coefficiente di assorbimento. A temperature elevate diventa importante la diffusione dei fotoni da parte di elettroni liberi. In tal caso si ha

Per decidere quale formula usare, conviene calcolare il flusso mediante le due formule e prender poi quella che dà il valore più piccolo.

b) Conducibilità elettrica

La conducibilità elettrica di un plasma in equilibrio dipende dall'esistenza di elettroni liberi. Sotto l'azione di un campo elettrico gli elettroni acquistano in media una certa velocità in direzione del campo, ma questo processo è disturbato dalle collisioni con gli ioni e gli atomi. In un plasma fortemente ionizzato la conducibilità elettrica risulta indipendente dalla densità. In questo caso la conducibilità (in ohm^-1 cm^-1) è data da

σ ≃ 10^-6T^3/2Z^-1.

Alle temperature tipiche dei plasmi, la conducibilità è dell'ordine di quella dei migliori conduttori metallici, argento e rame, a temperatura ambiente.

c) Campi magnetici nei plasmi

L'elevata conducibilità elettrica dei plasmi fa sì che, in condizioni stellari o galattiche, i campi magnetici generati dalle correnti che scorrono entro il plasma posseggano proprietà di notevole importanza. La resistenza elettrica tenderebbe a ridurre tali correnti, ma la conseguente diminuzione del campo magnetico genera una forza elettromotrice che tende a opporsi agli effetti dovuti alla resistenza. Ne risulta che la diminuzione di correnti e di campi, anche in un periodo di 10¹⁰ anni (il cosiddetto tempo cosmologico), è del tutto trascurabile nei più comuni oggetti astronomici. Questo fatto si esprime dicendo che il campo magnetico è ‛congelato' nel plasma. Nel corso dell'evoluzione stellare, quando una stella ordinaria raggiunge lo stadio di nana o di stella di neutroni, il flusso magnetico, cioè il prodotto del campo per la superficie caratteristica della stella, si conserva. Il campo, dell'ordine di un gauss sulla superficie del Sole, salirebbe a 10⁶ gauss per le dimensioni tipiche di una nana e a 10¹² gauss per una stella di neutroni. Questa è la spiegazione che Kardashev e Ginzburg dettero della presenza di forti campi magnetici in stelle di alta densità, ancor prima della scoperta delle pulsar.

d) La condizione di neutralità elettrica

In qual misura è lecito considerare un plasma come una miscela di due gas, quello degli ioni, pesante, e quello degli elettroni, praticamente senza massa? Non può avvenire che in alcuni casi, per esempio sotto l'azione della gravità, essi vengano separati in modo tale che gli ioni si concentrino in una certa regione e gli elettroni in un'altra? Le collisioni tra ioni ed elettroni non sono infatti così frequenti, soprattutto nei plasmi rarefatti e otticamente sottili, da impedire una tale separazione di ioni ed elettroni. La chiave per la comprensione del comportamento di un plasma è data dalle forze elettriche.

Un plasma è in media neutro finché in esso la densità degli ioni, moltiplicata per la loro carica, uguaglia ovunque l'analoga quantità relativa agli elettroni. Uno sbilanciamento, anche molto piccolo, tra le due densità porta subito alla formazione di cariche, campi elettrici e forze di valore altissimo. Per esempio, il Sole contiene circa 10⁵⁷ elettroni e 10⁵⁷ protoni. Se il numero degli elettroni superasse quello dei protoni dello 0,001%, la carica che si formerebbe sarebbe pari a 10³³ coulomb e il campo elettrico alla superficie varrebbe 3 × 10²³ volt/cm. La forza elettrostatica esercitata su un protone alla superficie sarebbe di 1012 dine, mentre lo stesso protone subisce una forza gravitazionale di sole 10^-19 dine. Ne consegue che uno sbilanciamento, apparentemente modesto, dello 0,001% è totalmente impossibile. I plasmi cosmici contengono sempre un ugual numero di cariche positive e negative e il plasma risulta elettricamente neutro.

e) Oscillazioni del plasma

Il problema della separazione delle cariche elettriche può essere posto anche in un'altra forma: ci si può chiedere infatti quale sarebbe l'evoluzione dello stato di un plasma in cui si verificasse una deviazione dalla neutralità elettrica. Langmuir ha dimostrato che in queste condizioni gli elettroni comincerebbero a muoversi in modo da neutralizzare la carica eccedente, ma a causa della loro inerzia continuerebbero poi nel loro movimento. Si instaurerebbero così delle oscillazioni a una frequenza caratteristica, detta ‛frequenza di Langmuir':

ν₀ = 9 × 10³ √-n,

dove ν₀ è data in hertz ed n, densità numerica media degli elettroni, in cm^-3. Una teoria precisa delle oscillazioni di un plasma rarefatto venne sviluppata da Vlasov e alcuni punti delicati vennero chiariti con acutezza da Landau.

L'esistenza di una frequenza caratteristica del plasma è di enorme importanza in astrofisica. Quando si considera la propagazione di radioonde, si trova che la velocità di propagazione è

v = c(1 −ν0²/ν²)^1/2

(dove v è la velocità di gruppo; la velocità di fase, u, sarà tale che uv = c²).

Per ν > ν₀ la formula ora scritta conduce a valori immaginari di v; la ragione fisica di questo fatto è assai chiara: onde con frequenza minore di ν₀ (cioè con lunghezza d'onda nel vuoto maggiore di c/ν₀) non possono propagarsi in un plasma avente densità n e frequenza di Langmuir ν₀; se queste onde incidono dallo spazio esterno su una regione in cui vi è il plasma, esse subiscono un effetto di riflessione totale. Questo fatto è importante per le comunicazioni radio: le onde radio possono infatti raggiungere tutti i punti della Terra grazie alla riflessione che subiscono da parte della ionosfera terrestre. D'altra parte le più lunghe fra le radioonde che provengono dallo spazio esterno vengono esse pure riflesse dalla ionosfera e ciò limita le possibilità della radioastronomia effettuata con strumenti al suolo a frequenze corrispondenti a lunghezze d'onda λ > 30 metri. Ponendo i ricevitori a bordo di satelliti artificiali si riesce a estendere lo spettro fino a λ ≃ 3 km. Oltre queste lunghezze d'onda la ricezione diventa molto difficile per effetto del plasma che forma il cosi detto ‛vento solare'.

Numerose ricerche effettuate di recente hanno mostrato che vi sono diversi agenti in grado di eccitare in un plasma oscillazioni con la frequenza caratteristica di Langmuir. Queste possono essere provocate da correnti intense, dall'azione meccanica di onde d'urto, da turbolenza, ecc.

Un plasma in cui siano state eccitate delle oscillazioni è, sotto molti aspetti, diverso da un plasma uniforme in equilibrio. Il moto collettivo di gruppi numerosi di elettroni può produrre un'intensa radiazione di frequenza doppia 2ν₀. La radioemissione delle pulsar è certamente dovuta al moto collettivo di gruppi numerosi di elettroni o di ioni o di elettroni e ioni. È anche possibile che la corrente indotta nel plasma dal campo magnetico rotante della stella di neutroni sia in grado di eccitare le oscillazioni del plasma. Anche la radiazione infrarossa delle quasar, recentemente scoperta, potrebbe essere connessa con oscillazioni del plasma, anche se, in questo caso, non si può escludere che sia dovuta all'emissione di singoli elettroni.

In un plasma che si trovi in uno stato eccitato, piccoli gruppi di particelle veloci possono assorbire energia dalle oscillazioni; è possibile che questo sia un meccanismo per la generazione dei raggi cosmici. Lo studio di un plasma eccitato con tutti i processi non lineari che in esso hanno luogo è il punto focale dell'astrofisica moderna.

f) Plasmi dominati dalla radiazione

Le proprietà di un plasma in cui prevalga la radiazione, come quello che si sarebbe avuto nelle fasi iniziali dell'evoluzione dell'Universo, sono molto importanti per la cosmologia.

Le forze gravitazionali sono causa di instabilità caratteristiche, in una distribuzione uniforme di materia; dovunque si abbia un aumento di densità, questa tende ancora a crescere a causa dell'aumentata attrazione gravitazionale: questo fenomeno era stato previsto già da Newton. È importante però tener conto che la pressione della radiazione si oppone alla tendenza della materia ad aggregarsi in oggetti distinti. Infatti, a causa delle frequenti interazioni tra fotoni ed elettroni, un aumento locale della densità di materia è accompagnato da un aumento della densità di radiazione e, di conseguenza, della pressione della radiazione. Quest'ultima può addirittura invertire il moto della materia che tendeva ad aggregarsi e produrre invece delle oscillazioni acustiche. Tra queste, quelle di piccola lunghezza d'onda sono fortemente attenuate per effetto della viscosità radiativa e solo quelle di lunghezza d'onda maggiore si mantengono nel tempo. Dopo la ricombinazione delle particelle, quando la radiazione non interferisce più con la materia divenuta neutra, la scala delle tipiche condensazioni di materia è fissata dalle onde acustiche sopravvissute ai periodi precedenti. Si vede quindi che, come conseguenza delle condizioni imposte dall'attenuazione radiativa, si formano aggregati di materia la cui massa è dell'ordine di 1014 masse solari, un valore cioè vicino a quello osservato per la massa degli ammassi di galassie. In questa teoria la strutturazione su scala più piccola, dalle galassie fino alle singole stelle, avviene successivamente a partire dal protoammasso già formato.

La teoria del plasma ha avuto un'importanza fondamentale durante tutta la secolare storia dell'astronomia. Le attuali conoscenze sulla struttura stellare si basano sulla teoria dei plasmi in equilibrio. Le proprietà del gas interstellare sono quelle caratteristiche di un plasma otticamente sottile. Le pulsar ci forniscono un esempio di forti eccitazioni collettive in un plasma magnetizzato e percorso da correnti. La cosmologia infine può essere inquadrata nel contesto dell'evoluzione di un plasma caldo costituito di particelle e antiparticelle.

(Si ringrazia il prof. Claudio Chiuderi per l'aggiornamento dell'articolo).

bibliografia

Akasofu, S.-J., Chapman, S., Solar-terrestrial physics, Oxford 1972.

Arzimovich, L.A., Sagdeev, R. Z., Plasma physics for physicists, Moskva 1979.

Gibson, E. G., The quiet sun, NASA 1973.

Kaplan, S. A., Pikelner, S. B., Physics of the interstellar matter, Moskva 1979.

Moffat, H. K., Magnetic field generation in electrically conducting fluids, Cambridge 1978.

Osterbrock, D.E., Astrophysics of gaseous nebulae, San Francisco 1974.

Parker, E. N., Cosmical magnetic fields, Oxford 1979.

Peebles, P. J. E., Physical cosmology, Princeton N. J., 1971.

Shlovskij, I. S., Supernovae, Moskva 1976.

Spitzer, L., The physics of fully ionized gases, Princeton, N. J., 1953.

Spitzer, L., Diffuse matter in space, New York 1968.

Weinberg, S., The first three minutes, New York 1977.

Zeldovich, Y.B., Novikov, I.D., Relativistic astrophysics, vol. I, Stars and gravitation, vol. II, Structure and evolution of the Universe, Chicago 1975-1981.

Zeldovich, Y.B., Rayzer, Y. B., The physics of shock waves and high temperature hydrodynamics, Moskva 1964.