poligono
poligono
poligono regione finita di piano delimitata da una poligonale piana chiusa. I segmenti che compongono la poligonale sono detti lati del poligono, i loro estremi vertici. La poligonale riferita al poligono è detta contorno del poligono.
Un poligono è detto intrecciato se due suoi lati non consecutivi si intersecano; un poligono non intrecciato è detto semplice. Un poligono semplice ha tanti angoli e tanti vertici quanti sono i suoi lati. Il poligono col minor numero di lati è il triangolo. Un poligono tale che tutti i suoi punti siano in uno stesso semipiano rispetto a ciascuna delle rette dei lati è detto poligono convesso, in caso contrario è detto poligono concavo. Un poligono concavo non può avere meno di quattro lati e deve possedere almeno un angolo maggiore di un angolo piatto. Esempio classico di poligono concavo è lo gnomone. Un particolare tipo di poligono intrecciato è quello stellato, di cui è un caratteristico esempio il pentagramma (→ pentagono). Se le bisettrici degli angoli interni di un poligono convesso passano tutte per uno stesso punto K esiste una e una sola circonferenza, detta circonferenza inscritta nel poligono, avente per centro K e tangente ai lati del poligono che, in tal caso, è detto poligono circoscritto alla circonferenza. Se gli assi dei lati di un poligono convesso passano tutti per uno stesso punto H, esiste una e una sola circonferenza, detta circonferenza circoscritta al poligono, avente per centro H e passante per tutti i vertici del poligono che, in tal caso, è detto poligono inscritto nella circonferenza.
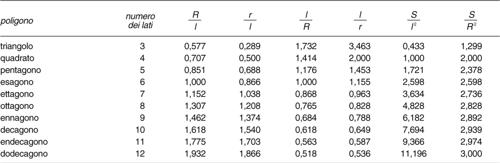
Un poligono convesso avente tutti i lati e tutti gli angoli di uguale misura è detto poligono regolare (per esempio, il quadrato); esso è equilatero ed equiangolo ed è sempre inscrivibile e circoscrivibile a una circonferenza (per la costruzione con riga e compasso dei poligoni regolari si veda → costruzione con riga e compasso). Le due circonferenze, inscritta e circoscritta a un poligono regolare, sono concentriche e il loro centro è detto centro del poligono. Il raggio della circonferenza circoscritta è detto raggio del poligono. In un poligono circoscrivibile a una circonferenza, il segmento di perpendicolare dal centro a un lato è detto apotema. Anche per poligoni (concavi) stellati si può definire una caratteristica di regolarità: un poligono regolare stellato è un poligono ottenuto per → stellazione da un poligono regolare quando tutti i segmenti esterni a esso tracciati hanno la stessa lunghezza.
I segmenti che congiungono due vertici non consecutivi sono detti diagonali del poligono e, per un poligono di n lati, sono in numero di n(n − 3)/2; in ogni vertice convergono (n − 3) diagonali. La somma degli angoli interni di un poligono convesso dipende dal numero n dei suoi lati e, in gradi, è uguale a (n − 2) ⋅ 180°, mentre la somma degli angoli esterni di un poligono convesso è pari a 360° qualunque sia il numero dei suoi lati. Per angolo esterno di vertice A si intende l’angolo supplementare all’angolo interno di vertice A, formato da uno dei lati che concorrono in A con la retta contenente l’altro lato concorrente in A. L’area di un poligono circoscrivibile a una circonferenza è data dal semiprodotto del perimetro per l’apotema.
A seconda del numero dei lati, delle ampiezze degli angoli e della uguaglianza o non uguaglianza tra lati o tra angoli un poligono convesso assume diversi nomi: triangolo, quadrilatero, pentagono, triangolo isoscele, triangolo rettangolo, quadrato, rombo ecc. L’area di un poligono è la misura della sua superficie nel piano, il perimetro di un poligono è la somma delle lunghezze dei suoi lati. Si dicono poligoni isoperimetrici due o più poligoni di uguale perimetro. Si dicono poligoni equiestesi due o più poligoni di uguale area. Due poligoni sono congruenti o uguali se esiste una isometria tale che a ogni punto del primo poligono corrisponda biunivocamente un punto dell’altro così che tutti i lati e gli angoli corrispondenti abbiano uguali misure; due poligoni sono simili se hanno angoli corrispondenti uguali e lati corrispondenti proporzionali; sono equivalenti se hanno la stessa area. Per stabilire se due poligoni con lo stesso numero di lati sono uguali o simili si scompongono in triangoli, tracciando tutte le diagonali da due vertici omologhi, e si applicano poi i criteri di congruenza o di similitudine dei triangoli a ogni coppia omologa risultante dalla scomposizione (→ congruenza, criteri di (per i triangoli)). Per particolari poligoni esistono formule che permettono di calcolarne l’area a partire dalla misura di alcuni elementi del poligono dato (→ area). Per esempio, l’area di un triangolo è data dal semiprodotto della base per l’altezza, l’area di un parallelogramma dal prodotto di base e altezza ecc.
In geometria proiettiva, è detto poligono piano completo la figura individuata da n punti di un piano (vertici), a tre a tre non allineati, e dalle n(n − 1)/2 rette che li congiungono a due a due.