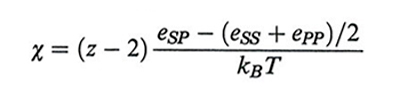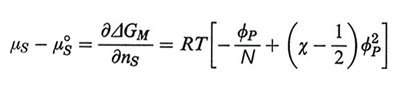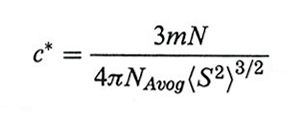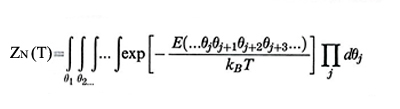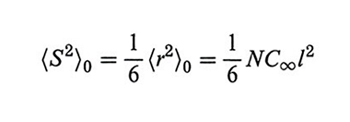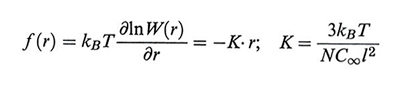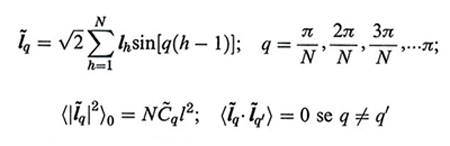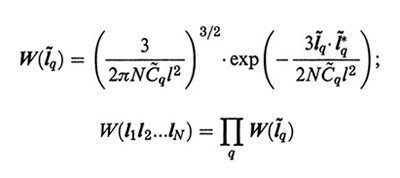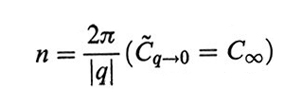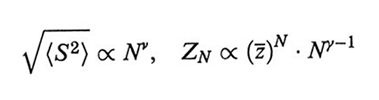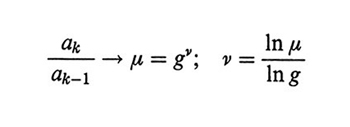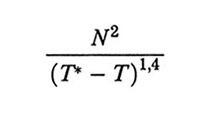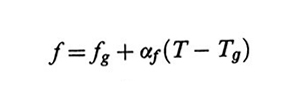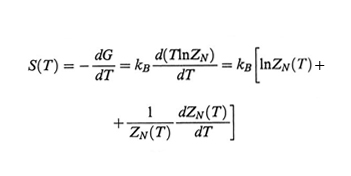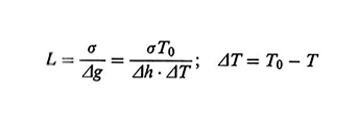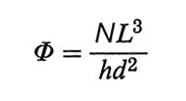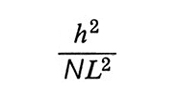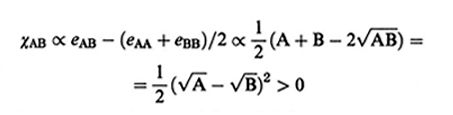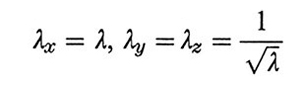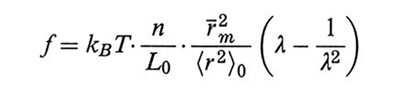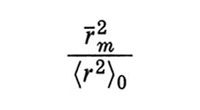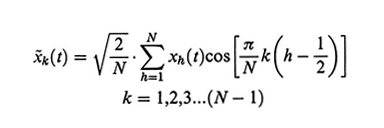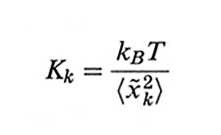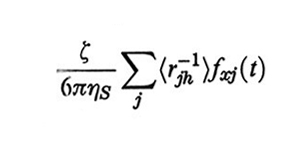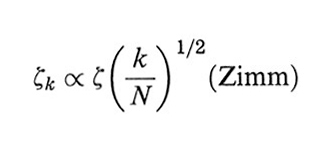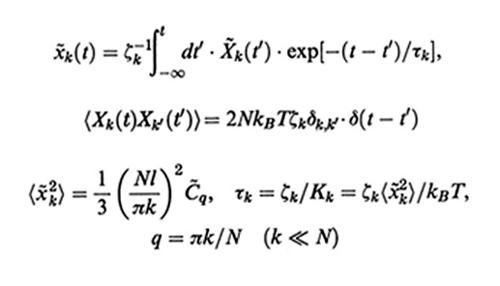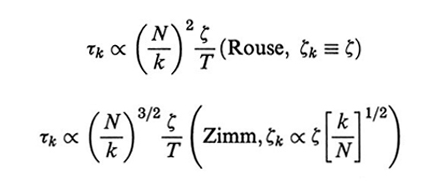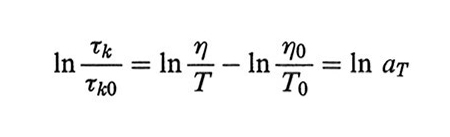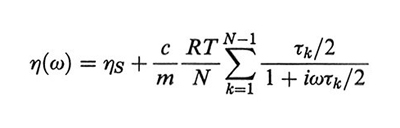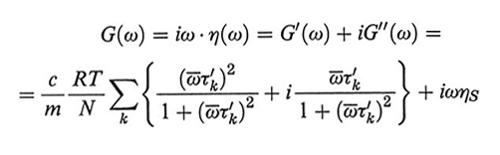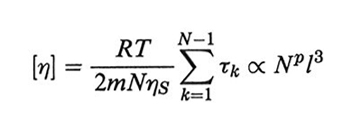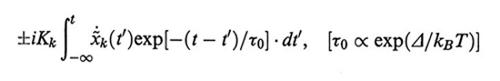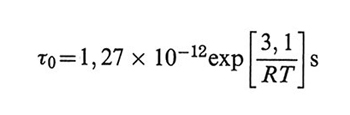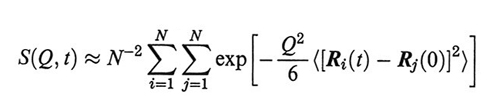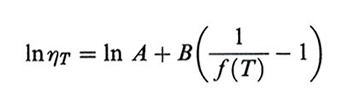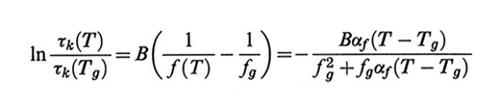Polimeri

Polimeri

Aspetti chimico-fisici

SOMMARIO: 1. Introduzione. 2. Le proprietà chimico-fisiche dei polimeri all'equilibrio: a) polimeri in soluzione; b) polimeri in massa. 3. Le proprietà dinamiche dei polimeri: a) soluzioni diluite; b) polimeri fusi e soluzioni concentrate. 4. Prospettive future. □ Bibliografia.

1. Introduzione

I polimeri - componenti fondamentali di molte sostanze, sintetiche o naturali - sono materiali tra i più innovativi del mondo moderno. Secondo la definizione della IUPAC (International Union of Pure and Applied Chemistry), "un polimero è una sostanza composta da molecole caratterizzate dalla ripetizione multipla di una o più specie di atomi o gruppi di atomi (unità di ripetizione costituzionali) legate l'una all'altra in quantità sufficiente a produrre un insieme di proprietà che non variano in modo apprezzabile per l'aggiunta di una o alcune unità". Quando la generica unità deriva dalla trasformazione chimica di una molecola originaria, detta monomero, essa può essere denominata unità monomerica. Ad esempio, nel caso del polietilene [...−CH₂−CH₂−CH₂−CH₂−...] l'unità monomerica à −CH₂−CH₂−, in quanto deriva dal monomero etilene CH₂=CH₂, mentre la più piccola unità di ripetizione costituzionale è −CH₂−. Nel seguito supporremo per semplicità che l'unità di ripetizione corrisponda a un solo legame di catena e che ogni catena abbia N legami.

Le macromolecole polimeriche possono essere lineari o ramificate. Se non ci sono gruppi reattivi che possano produrre legami tra le diverse macromolecole, il polimero si dice 'termoplastico', perché la forma esterna dei manufatti può essere modificata mediante riscaldamento. Se invece le macromolecole contengono gruppi reattivi, il polimero può appartenere alla classe delle 'resine termoindurenti', le quali, a temperature abbastanza elevate, formano un reticolo tridimensionale di legami covalenti che ne determina il progressivo indurimento. Nel seguito ci occuperemo essenzialmente di polimeri termoplastici e ci limiteremo per semplicità alle catene lineari.

fig. 1

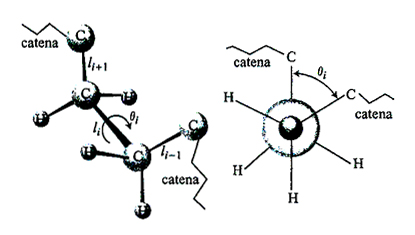
La struttura stereochimica di una macromolecola lineare è determinata dalla sua costituzione, o modo di concatenazione tra i suoi atomi, e dalla sua configurazione, o modo di successione dei centri di stereoisomeria. Questi ultimi possono essere atomi che portano due sostituenti diversi (e possono, quindi, disporsi in due possibili modi rispetto alla catena, come nel caso del polipropilene), oppure doppi legami che possono avere configurazione cis o trans. La forma effettivamente assunta dalla macromolecola (ad esempio rettilinea, a elica, o più o meno ripiegata) è invece definita 'conformazione' ed è specificata dall'insieme degli angoli di rotazione interna θ_i (v. fig. 1). Lunghezze e angoli di legame si possono di regola ritenere fissi dato che le costanti elastiche delle forze di richiamo all'equilibrio hanno valori relativamente elevati.

Nel seguito si presenterà un'analisi teorica di alcuni importanti aspetti chimico-fisici dei polimeri. Non saranno invece discussi i risultati di simulazioni al calcolatore, pur se attualmente rappresentano un efficacissimo strumento complementare di analisi, in rapida espansione.

2. Le proprietà chimico-fisiche dei polimeri all'equilibrio

a) Polimeri in soluzione.

fig. 3

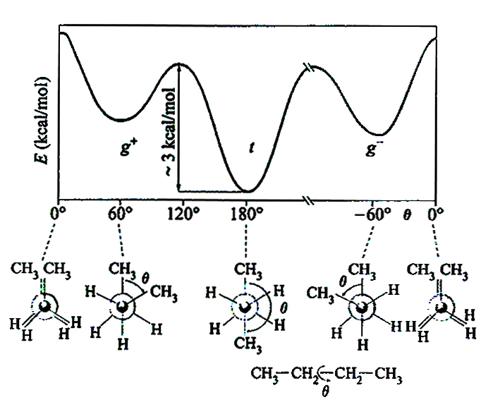
1. Il segmento statistico. - Verranno in genere considerate soluzioni diluite, cioè tali che i gomitoli generati dalla conformazione casuale delle diverse macromolecole non si sovrappongano e ognuna di esse contribuisca in modo additivo alla proprietà misurata, ad esempio la viscosità o lo scattering della luce. I valori più probabili dell'angolo di rotazione interna θ attorno al generico legame di catena corrispondono a minimi locali dell'energia - ad esempio le configurazioni t (trans) g⁺ e g^- (gauche positiva o negativa) nel caso di un polimero idrocarburico; v. fig. 2 - dovuti soprattutto all'interazione tra gli elettroni di legame. L'energia conformazionale è anche influenzata da interazioni tra atomi non legati, come ad esempio quelle espresse dai potenziali Lennard-Jones; ne deriva una correlazione tra i vettori di legame successivi l_i, cioè un valore non nullo del prodotto scalare medio 〈l_i • l_i+k〉 che, comunque, da un certo valore di k in poi diminuisce sempre con continuità. Il segmento statistico può essere definito come una sequenza di k* legami, tale che k* sia il minimo valore di k al di sopra del quale il prodotto scalare ha valore trascurabile. La porzione di catena compresa nel segmento statistico si può ritenere statisticamente indipendente dalla precedente e dalla seguente; nella fig. 3, ad esempio, i vettori L₁, L₂, L₃ sono tra loro scorrelati in quanto 〈L_i • L_j〉 = 0 per i ≠ j.

Il concetto di segmento statistico permette di dare una descrizione omogenea, o generale, della catena polimerica considerata molto lunga: tutte le catene in soluzione diventano statisticamente simili se si identifica l'unità di scala con la radice quadratica media L della lunghezza dei loro segmenti statistici. La catena che ne risulta può essere descritta come un gomitolo statistico generato dai segmenti statistici che, in successione, percorrono un cammino casuale (random walk).

2. La teoria Flory-Huggins. - Nello studio termodinamico delle soluzioni è cruciale il calcolo dell'entropia del sistema. La teoria Flory-Huggins utilizza il metodo reticolare, che permette di contare le configurazioni spaziali delle molecole in base al riempimento delle celle di un reticolo regolare. Ogni cella del reticolo può ospitare una molecola di solvente oppure un segmento statistico del polimero (v. fig. 4), e segmenti consecutivi debbono essere collocati in celle adiacenti. Utilizzando il modello di soluzione regolare, per cui a tutte le configurazioni viene data la stessa probabilità (o peso) anche se non hanno necessariamente la stessa energia, si ottiene

∆S_M = - R(n_slnϕ_s + n_Plnϕ_P).    (1)

Gli indici S e P corrispondono a solvente e polimero, n_X e ϕ_X sono rispettivamente il numero di moli e la frazione in volume (v. Flory, 1953); quest'ultima sostituisce la frazione molare che appare nella teoria delle soluzioni. Indicando con e_SS, e_PP ed e_SP le energie di interazione tra celle adiacenti contenenti solvente o polimero, e con z il numero di coordinazione del reticolo (z = 6 nel reticolo cubico), il parametro χ di Flory è definito come

formula  (2)

Tenendo conto della (1) e assumendo ϕ_P ≪ 1, il potenziale chimico del solvente è

formula (3)

dove N è il numero di segmenti statistici nella catena e μ_S⁰ è il potenziale chimico del solvente puro. Il termine in ϕ_P² è legato alle interazioni fra coppie di segmenti della catena, e pertanto, se χ = 1/2 tali interazioni sono assenti (idealità della soluzione; v. sotto, punto 3). Il termine lineare in ϕ_P è lo stesso che si ha per le sostanze ordinarie; poiché le normali proprietà colligative dipendono da (μ_S - μ_S⁰, per χ = 1/2 o per piccoli valori di ϕ_P esse discendono solo dalla concentrazione molare del polimero, indipendentemente dal suo peso molecolare. Pertanto dalla loro misura si può ricavare la media numerale M_n del peso molecolare, ovvero la media che si ottiene dando lo stesso peso a catene di diversa lunghezza.

3. Le soluzioni diluite e la soluzione ideale. - Se indichiamo con 〈S²〉 il raggio quadratico medio di girazione di una catena, una soluzione è diluita se la sua concentrazione c (g/l) è inferiore al valore critico c* per cui si ha il contatto tra i gomitoli polimerici:

formula,  (4)

dove m ed N sono rispettivamente la massa molare per legame di catena e il numero di legami, mentre N_Avog è il numero di Avogadro. Abbiamo visto che, se χ = 1/2 (cioè se la soluzione è lievemente endotermica), si annulla l'interazione a coppie tra segmenti diversi della catena. Si può dire che l'espansione di catena dovuta al volume escluso (impossibilità di rioccupare celle già attraversate) viene compensata da un corrispondente effetto di contrazione. La temperatura Θ per la quale ciò si verifica è anche detta ideale ed è specifica della coppia solvente-polimero: si parla in tal caso di polimero imperturbato. In questo stato, su una scala spaziale sufficientemente grande, la catena segue un cammino casuale e la distanza quadratica media tra due suoi punti è proporzionale alla lunghezza di catena che li separa. Se r è la distanza tra gli estremi, N ed l il numero dei legami di catena e la loro lunghezza, rispettivamente, si ha

〈r₂〉₀ = NC∞l²  (5)

dove il suffisso 0 indica lo stato ideale e C_∞ è il rapporto caratteristico, calcolabile assumendo che l'energia della catena sia dovuta a contributi locali indipendenti. La funzione di partizione Z_N(T) - che permette di ottenere le diverse medie statistiche - è data da

formula  (6)

dove E(...θ_j θ_j+1θ_j+2θ_j+3…) è l'energia della generica conformazione della catena, definita dagli angoli di rotazione interna θ_j. Di norma i termini energetici più importanti sono dovuti a coppie di rotazioni successive, e si può scrivere:

E(...θ_j θ_j+1θ_j+2θ_j+3…) = ...+ E(θ_j θ_j+1)  + E(θ_{j +1}θ_j+2) + E(θ_j+2θ_j+3) + ...   (6a)

L'energia E(θ_jθ_j+1) è generalmente calcolata con i metodi della meccanica molecolare. Il metodo degli stati isomerici rotazionali, proposto da Paul John Flory (v., 1969) e dalla sua scuola e largamente applicato, consiste nel calcolare l'integrale configurazionale come somma sui soli minimi energetici locali; la funzione di partizione è una somma di potenze di matrici i cui elementi sono i pesi statistici w(θ_jθ_j+1) = exp [-E(θ_jθ_j+1)/k_BT] (v. Lifson, 1959). (Nel caso dei copolimeri statistici nasce il delicato problema, detto copolymer problem, in sostanza ancora aperto, di calcolare la funzione di partizione media tenendo conto della distribuzione statistica delle unità comonomeriche). È possibile ottenere l'integrale configurazionale in modo completo mediante rappresentazione di w(θ_jθ_j+1) in doppia serie di Fourier; il metodo delle matrici di correlazione che ne deriva può essere vantaggioso quando, in unità k_BT, i minimi di energia sono larghi o mal definiti (v. Allegra e Immirzi, 1969). I valori usuali di C_∞, sia sperimentali, sia calcolati tramite le medie statistiche, sono compresi tra ~ 5 e alcune decine, crescendo per polimeri più rigidi. La lunghezza L del segmento statistico è ottenuta da C_∞ supponendo che la lunghezza Nl di massima estensione della catena sia eguale alla lunghezza totale NL di tutti i segmenti connessi tra loro. Si ha

formula.  (7)

La distanza quadratica media testa-coda tra gli estremi della catena allo stato ideale 〈r²〉₀ è importante sul piano sperimentale perché è legata in maniera semplice al raggio di girazione quadratico medio 〈S²〉₀, misurabile mediante light scattering:

formula.  (8)

La densità di probabilità 4πr²W(r) che la distanza testa-coda |r| abbia il valore r è ottenibile dal teorema del limite centrale; essa permette, come vedremo, di calcolare la forza attrattiva che la catena può esercitare su due punti materiali collegati alle sue estremità. Se il numero N di segmenti è grande, la distribuzione di probabilità della variabile aleatoria r = L₁ + L₂ + … + L_N è una gaussiana, con media e varianza date rispettivamente dalla somma delle medie e delle varianze dei vettori L_k. Si ottiene, con l'uso della (7) e di 〈L_k〉 = 0, 〈L_k²〉 = L²:

formula.  (9)

La forza ± f(r) necessaria a mantenere gli atomi estremi della catena alla distanza r è data da

formula,  (10)

da cui si vede che la catena ideale si comporta come una molla hookeana perfetta.

Per descrivere la statistica delle conformazioni locali della catena, è necessario introdurre i modi normali, definibili come

formula  (11)

La densità di probabilità W(l₁l₂…l_N) che la conformazione della catena sia l₁...l_N è data dal prodotto di tutte le probabilità gaussiane dei modi normali:

formula  (11

a)

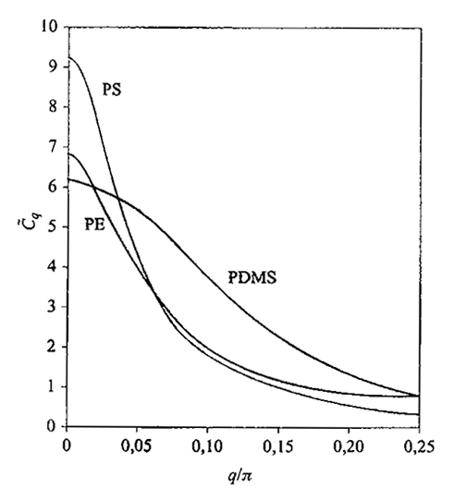
Il rapporto C~_q generalizza C_∞ in quanto ne rappresenta il valore effettivo quando si considerano sequenze di catena con un numero finito di legami

fig. 5

La fig. 5 riporta i grafici di C~_q calcolati per alcuni polimeri: la presenza di un picco stretto all'origine (q ~ 0) implica la tendenza alla rigidità locale della catena, in quanto per sequenze abbastanza corte l'asse medio della catena tende a persistere nella sua direzione: per queste distanze di osservazione si ha la cosiddetta worm-like chain. Questa proprietà viene meno quando la sequenza di catena che si considera è più lunga di

formula

legami, dove q* è la coordinata del punto di flesso di C~_q, nel qual caso si ha il vero e proprio modello a cammino casuale (random walk). Come vedremo nella dinamica, la funzione C~_q è anche legata alla forza elastica dei modi locali di deformazione della catena.

Flory (v., 1953) ha dimostrato che lo stato ideale si realizza in buona approssimazione in un polimero fuso o amorfo; l'argomento basilare è che in tale stato un segmento del polimero non può 'capire' se i segmenti circostanti appartengano o no alla sua stessa catena, e pertanto si orienta in modo casuale. La previsione è stata ampiamente confermata da esperimenti di scattering di neutroni su campioni parzialmente deuterati.

4. Lo stato di buon solvente. - In questo caso si ha χ<1/2 e le interazioni polimero-solvente sono energeticamente favorite (v. eq. 3). Nel caso di polimeri che non hanno forti interazioni polari, come ad esempio polietilene, polipropilene e polistirolo, questa condizione si verifica per T > Θ, ma per polimeri polari può accadere l'inverso. Le catene sono circondate da molecole di solvente e aumentano il loro volume effettivo (solvatazione); le conformazioni relativamente espanse sono le più probabili, perché la catena riesce in questo caso a ridurre l'effetto del volume escluso, ovvero l'auto-intersezione dei suoi segmenti nello spazio. Dopo un primo studio pionieristico e fondamentale di Flory (v., 1949), il difficile problema del volume escluso è stato oggetto di un gran numero di studi ed è stato trattato anche con metodologie raffinate, come le tecniche del gruppo di rinormalizzazione introdotte da Kenneth Wilson per lo studio della teoria dei campi (v. Wilson e Kogut, 1974).

Il risultato di Flory è esprimibile con un'unica legge di potenza che lega il raggio quadratico medio di girazione 〈S²〉 al numero N di legami della catena (per N grandi), qualunque sia il valore di χ < 1/2:

〈S²〉 = K(χ) ∙ N^6/5;   (12)

il valore di χ influenza soltanto il pre-fattore K. La linea logica di Flory è semplice: indichiamo con α > 1 il coefficiente di espansione lineare della catena rispetto allo stato ideale (α = 1); l'espansione implica un aumento di energia libera di tipo elastico. Assumendo che tutte le distanze fra atomi della catena si distribuiscano in modo gaussiano, come avviene nello stato ideale, l'energia libera elastica è approssimativamente eguale alla seguente espressione (positiva per α ≠ 1):

Gel = 3/2KbT(α²- 1 - ln α²),   (13)

mentre l'energia libera dovuta alle interazioni fra i segmenti è data da

G_intra ∝ N∙(densità)∝V^1/2/α³  (14)

Scrivendo G = G_el + G_intra e ponendo ∂G/∂α = 0, per N grandi si ottiene α ∝ N^1/10. Ricordando dalla (8) che 〈S²〉₀ ∝ N, si ha 〈S²〉 = 〈S〉₀ • α² = K • N^6/5, cioè il risultato (12). A meno di fattori logaritmici relativamente deboli, che descrivono ulteriori aumenti delle distanze tra segmenti vicini nella sequenza di catena, il risultato di Flory è stato sostanzialmente confermato in studi successivi, considerando tutti i modi normali di deformazione entro l'approssimazione gaussiana (v. eqq. 11 e 11a); oggi sappiamo che il valore esatto dell'esponente è 2ν = 1,176 (v. eq. 17).

fig. 6

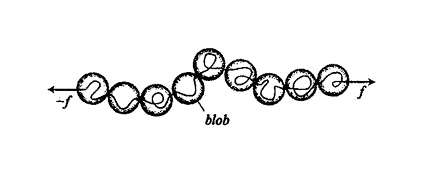
Nell'ambito della teoria del gruppo di rinormalizzazione, in un buon solvente una macromolecola con N → ∞ è considerata un sistema critico, nel senso che le interazioni, repulsive, coinvolgono tutte le coppie di segmenti comunque grande sia il loro numero. Ne derivano alcune leggi di scala, ovvero relazioni tra grandezze fisiche del sistema sotto forma di leggi di potenza valide a tutte le scale, i cui esponenti sono detti esponenti critici. La giustificazione concettuale delle leggi di scala è data dalla auto-similarità della catena: essa appare sempre simile a se stessa se vista da diverse distanze di osservazione, purché abbastanza grandi. L'auto-similarità viene meno se la scala di osservazione diventa comparabile alla lunghezza del segmento statistico, perché allora le sequenze di catena non sono influenzate dagli effetti del volume escluso. Per queste sequenze è stato suggerito il termine blobs (v. fig. 6); la dimensione dei blobs può essere valutata, ad esempio mediante l'analisi dei modi normali di deformazione. È naturale che tale dimensione sia sempre più piccola quanto più grande è la forza del solvente, espressa dal termine (1/2 - χ) nella (3). Tra gli esponenti critici più importanti ci sono ν e γ, definiti, per una catena di N legami (N → ∞), da

formula  (15)

dove Z_N è la funzione di partizione (ovvero, in questo caso, il numero di configurazioni permesse) e ž è un numero dell'ordine di qualche unità, dipendente dal tipo di reticolo impiegato.

I metodi di rinormalizzazione possono essere applicati seguendo la strategia della rinormalizzazione iterativa o quella della rinormalizzazione analitica, che descriveremo brevemente (v. de Gennes, 1979; v. des Cloizeaux e Jannink, 1987).

Nel caso della rinormalizzazione iterativa si raggruppano i segmenti in N/g sottounità, dove g è un numero intero opportuno, quindi si raggruppano le sottounità in nuove sottounità g-volte più grandi, e così via iterativamente. Per ogni iterazione k (= 1,2,3...) si calcola sia la dimensione media a_k delle sottounità che l'energia di interazione e_k di ognuna di esse. Per k tendente a infinito, la densità di energia rinormalizzata u_k = e_k/a_k^d (d = 3 nello spazio ordinario) tende a un valore costante che corrisponde al punto fisso u* della procedura di rinormalizzazione. In queste condizioni, detto μ il limite del rapporto a_k/a_k-1, l'esponente ν definito nella (15) è dato da

formula  (16)

e una stima ragionevole si può ottenere già dalle prime iterazioni.

Nella rinormalizzazione analitica, poiché in quattro dimensioni (d = 4) l'effetto di volume escluso è nullo, le opportune grandezze medie della catena si calcolano come serie di perturbazioni nella variabile ε = 4 - d a partire dal loro valore a ε = 0. In genere i calcoli vengono condotti utilizzando il modello di Landau-Ginzburg (v. Landau e Lifshitz, 1958), che utilizza l'espressione dell'energia libera nello spazio reciproco, coniugato allo spazio reale tramite trasformata di Fourier; il vettore coniugato k corrisponde all'inverso della dimensione della catena: si calcolano le interazioni intramolecolari per diversi diagrammi topologicamente distinti, che corrispondono a contatti multipli tra i segmenti. Valori divergenti, dovuti alle coppie di segmenti vicini tra loro, vengono eliminati introducendo dapprima una distanza di troncamento (regolarizzazione) e poi eliminando tale distanza attraverso un numero finito di rinormalizzazioni (v. Freed, 1987; v. des Cloizeaux e Jannink, 1987). Gli esponenti critici, tra cui ν e γ (v. eq. 15), vengono calcolati per una catena infinitamente lunga tramite il limite |k| → 0. Nel caso tridimensionale (ε = 1) Jean-Claude Le Guillou e Jean Zinn-Justin (v., 1985) hanno ottenuto:

ν = 0,5880 ± 0,0010;  γ = 1,1615 ± 0,0011   (17)

Sulla base di elaborazioni numeriche in 3 dimensioni, Cyril Domb e altri (v., 1965) hanno proposto la seguente distribuzione W(R) della distanza tra due atomi la cui radice quadratica media sia R̄:

formula  (18)

Questa distribuzione ha trovato conferma anche in studi teorici; i parametri θ e δ sono da considerarsi esponenti critici. In uno studio basato sull'analisi dei modi normali, con ampiezze x distribuite secondo la densità di probabilità esponenziale non gaussiana exp(-αx²-βx⁴), ottimizzando l'energia libera della catena si sono ottenuti i risultati θ = 0,37, ν = 0,593 (v. Allegra e Colombo, 1994). Mentre ν è in buon accordo con la (17), il valore di θ proposto si discosta alquanto da quello ottenuto da altri autori. Ad esempio, de Gennes (v., 1979) propone l'equazione νθ = γ - 1 da un'analisi statistica fondata sulla probabilità di contatto fra due atomi della catena disposti su un reticolo, ottenendo così θ = 0,27 dai dati della (17).

fig. 7

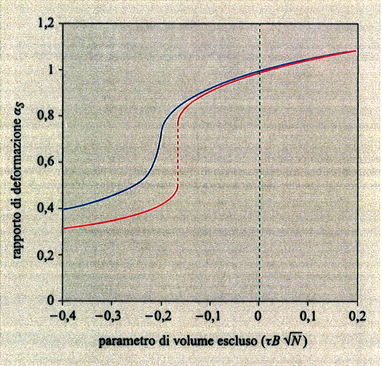
5. Polimeri in cattivo solvente: collasso, separazione di fase. - Se il solvente è cattivo (χ > 1/2), cioè per T < Θ con polimeri poco polari, la soluzione tende a separarsi in due fasi (v. fig. 7). Nella fase più concentrata le catene sono vicine allo stato imperturbato; infatti, le interazioni fra coppie di atomi sono scarsamente modificate da un'espansione o una contrazione dei gomitoli polimerici, dal momento che essi si sovrappongono. Nella fase diluita le catene sono contratte (collassate) e la loro concentrazione è spesso così bassa che è difficile avere dati attendibili da light scattering, ad esempio, per la debolezza del segnale. Inoltre, come è stato dimostrato sperimentalmente (v. Chu e altri, 1988 e 1995) e come sarà discusso più avanti, la cinetica della contrazione delle catene è non solo assai lenta, ma è inoltre complicata dall'aggregazione tra le catene, il cui tempo caratteristico è confrontabile con quello della contrazione stessa.

fig. 8

fig. 9

fig. 10

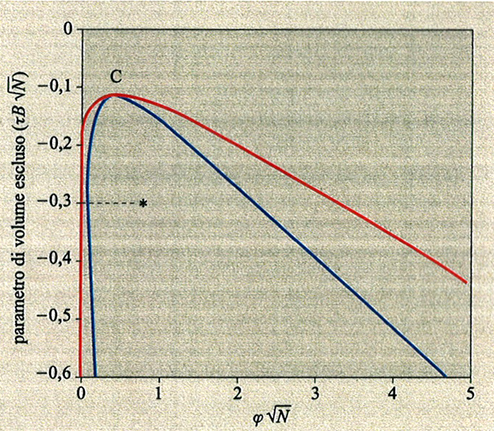
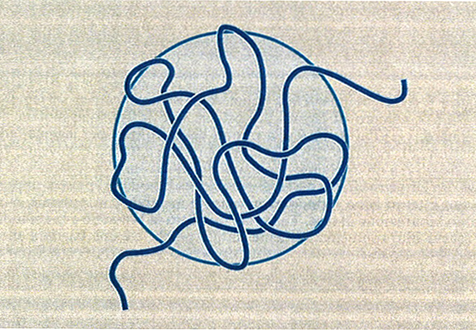
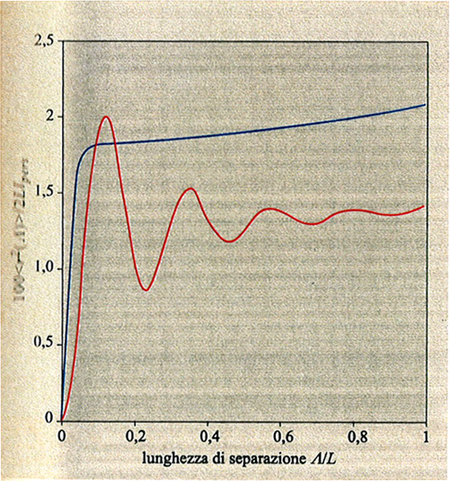
La fig. 8 mostra il grafico del rapporto α_S = S̄ /S₀ (S̄ e S̄₀ sono i raggi medi di girazione della catena isolata alle temperature T e T = Θ, rispettivamente) al variare del parametro di volume escluso τ B√N, con τ = (T - Θ)/T (v. anche fig. 7). È interessante notare che, nel limite termodinamico N → ∞, tutti e tre gli stati (collassato T < Θ, ideale T = Θ ed espanso T > Θ) si realizzano in un unico intorno infinitesimo della temperatura Θ, giustificando così la denominazione di temperatura tricritica. L'espansione (T > Θ) e il collasso (T < Θ) non sono tra loro simmetrici, perché la prima avviene con gradualità, mentre il collasso è più brusco e ha il carattere di una transizione del primo ordine se la catena è relativamente rigida e sottile (curva rossa in fig. 8). Il′ja Lifshitz e collaboratori (v. Grosberg e Khokhlov, 1994) hanno dimostrato che la variazione di entalpia ΔH al collasso è proporzionale a √N, e non a N come ad esempio nelle normali trasformazioni liquido-gas. Di conseguenza, per intervalli di temperatura di pochi gradi al di sotto e al di sopra di Θ, le differenze di energia libera tra stato imperturbato e stato collassato sono inferiori a k_BT; questo conduce a grandi fluttuazioni nella dimensione della catena, in contrasto con le normali transizioni del primo ordine. La configurazione statistica della catena nel globulo collassato (v. fig. 9) è diversa a seconda che il rapporto tra il raggio medio S̄ e la lunghezza del segmento statistico L sia molto maggiore di 1 oppure dell'ordine di 1. Nel primo caso (ad es. polistirolo ad alto peso molecolare, comportamento flessibile) la distanza quadratica media <r²(Λ)> tra due atomi separati da una lunghezza di catena Λ cresce rapidamente fino a un determinato valore e rimane quasi costante con l'aumentare di Λ (v. fig. 10); i terminali di catena sono di preferenza spinti sulla superficie, o fuori di essa (v. fig. 9). Nel secondo caso (catena localmente rigida), come si vede dalla curva rossa in fig. 10, si hanno oscillazioni i cui massimi corrispondono a segmenti statistici successivi. È interessante menzionare il fatto che i dati medi presi dalla struttura cristallina di una trentina di frammenti globulari di diverse proteine sono in discreto accordo con questo grafico, e ciò suggerisce che il cosiddetto folding delle proteine possa essere considerato una specie di fluttuazione statistica rispetto al comportamento medio di una catena omogenea collassata.

La cinetica della catena che collassa è stata studiata teoricamente, tra gli altri, da Pierre-Gilles de Gennes (v., 1985), Alexander Y. Grosberg (v. Grosberg e altri, 1988) e Fabio Ganazzoli (v. Ganazzoli e altri, 1995). I primi due autori considerano un meccanismo a due stadi: nel primo stadio (per il quale de Gennes usa la metafora della 'salsiccia che si rigonfia') la catena si contrae longitudinalmente e si accresce lateralmente; nel secondo la catena si ristabilizza tramite un complesso meccanismo, disfacendo i propri nodi e riequilibrandosi con movimenti 'a rettile' lungo il proprio asse (reptation). Sia nel lavoro di de Gennes che in quello di Grosberg il tempo caratteristico complessivo risulta essere proporzionale a (T* - T), dove T* e T sono, rispettivamente, la temperatura critica del collasso e quella effettiva. Anche secondo l'analisi di Ganazzoli - che è invece basata sulla risoluzione numerica delle equazioni di moto dei vari modi normali (v. eq. 11) - il collasso della catena è separabile in due fasi: mentre nella fase di induzione solo i modi normali locali (q grande) contraggono significativamente le loro ampiezze quadratiche medie, così che la dimensione della catena non varia apprezzabilmente, nella seconda fase il collasso complessivo è estremamente veloce, probabilmente dovuto a un meccanismo autocatalitico. Il tempo caratteristico è proporzionale a

il che indica che il collasso è tanto più veloce quanto più la temperatura si avvicina a T*, entro limiti appropriati. I dati sperimentali di Benjamin Chu e collaboratori (v. Chu e altri, 1995) sembrano in buon accordo con questo quadro. Sorprendentemente, alcuni di questi dati possono essere interpretati ammettendo che globuli comprendenti più di una catena (clusters) possano avere un diametro inferiore a quello di una catena singola. Infatti, la variabile termodinamica che determina il collasso è x = (Θ - T) √N (v. fig. 8) e la formazione di un cluster aumenta il valore efficace di N, accrescendo pertanto x per valori della temperatura fissati (v. Grosberg e Khokhlov, 1994; v. Raos e Allegra, 1996).

6. Le soluzioni concentrate, i gel. - Quando la concentrazione della soluzione supera il valore c*, corrispondente all'inizio della sovrapposizione tra i gomitoli polimerici, la conformazione media delle singole catene tende verso lo stato ideale, mentre la qualità del solvente diventa sempre meno importante. A titolo di esempio, il valore di c* può essere facilmente calcolato nel caso di solvente atermico (cioè, di fatto, buon solvente) in cui la catena avverte l'espansione di volume escluso (χ = 0; v. eq. 3). Poiché c* è proporzionale all'inverso del volume occupato dalla singola catena, dalle equazioni (4) e (12) si ha

c*∝ N/Sˉ̄³∝ 1/[N^4/5 C^3/2∞l³].  (19)

Un polimero può manifestare la tendenza ad assorbire molto solvente dando luogo a un gel; si tratta di solito di polimeri e solventi polari. Le proprietà elastiche dei gel sono simili a quelle delle gomme vulcanizzate (v. sotto, §b, punto 5); nel primo caso il reticolo polimerico è stabilizzato da allacciamenti temporanei fra le catene, nel secondo da giunzioni permanenti in forma di legami chimici dovuti alla vulcanizzazione.

7. I polimeri in spazi confinati. - Lo studio del confinamento di macromolecole entro spazi, cilindrici o sferici, limitati da superfici parallele è attualmente ritenuto rilevante per la scienza dei nanomateriali. Uno dei primi studi sistematici in questo campo (v. Casassa, 1967) è stato suggerito dalla cromatografia a esclusione dimensionale (size-exclusion chromatography). Usando il metodo dell'equazione di diffusione applicata al cammino casuale della catena, viene calcolata l'energia necessaria a confinare tra pareti piane parallele una lunga catena in un solvente ideale. A partire da queste basi teoriche è possibile studiare la correlazione fra volume di eluizione, cioè il volume di soluzione che deve passare in una colonna cromatografica, e il peso molecolare della frazione del polimero che si osserva in corrispondenza: più grande è la catena, più piccolo il suo volume di eluizione, perché essa non riesce a inserirsi nelle microcavità del riempimento cromatografico e quindi viene espulsa rapidamente dalla colonna. Successivamente Edmund DiMarzio (v., 1965 e 1971) ha dimostrato che si possono ottenere i precedenti risultati con un modello di catena su reticolo cubico, risolvendo il problema agli autovalori della corrispondente matrice di transizione. Se le pareti hanno un potenziale attrattivo per gli atomi della catena, esiste una temperatura di transizione

formula,

dove ε è il potenziale attrattivo (< 0) per ogni sito del reticolo a contatto con una parete. Per T < T* la catena infinita si concentra (collassa) in vicinanza delle pareti, per T = T* essa occupa lo spazio tra le pareti con densità uniforme, e per T > T* viene respinta dalle pareti concentrandosi nello spazio intermedio.

Mentre negli studi di Edward Casassa e di DiMarzio il polimero è considerato in soluzione ideale, Jan Scheutjens e Gerard Fleer (v., 1979 e 1980) affrontano anche il problema del volume escluso, dimostrando tra l'altro che i terminali di catena si estendono verso la zona intermedia tra le pareti a differenza dei segmenti centrali. Utilizzando ancora il modello reticolare e vincolando in maniera autoconsistente la densità del polimero nelle diverse zone della fenditura, questi autori studiano la percentuale di superficie ricoperta e la frazione di polimero adsorbito, per diverse lunghezze della catena. Altri autori (v. Wang e altri, 1987) utilizzano metodi basati sulla rinormalizzazione per studiare il comportamento di una catena in presenza di una parete, assumendo che sia penetrabile o meno, attrattiva o repulsiva. È stato studiato, sia analiticamente che mediante simulazioni, il caso di catene adsorbite da superfici con asperità (v. Baumgärtner e Muthukumar, 1987), e il caso di catena in buon solvente tra pareti attrattive (v. Allegra e Colombo, 1996), dimostrando che, per opportuni valori della temperatura e del volume escluso, il polimero, a seconda della larghezza della fenditura, può esercitare a sua volta una forza attrattiva sulle pareti oppure una forza sempre repulsiva, in accordo qualitativo con le accurate osservazioni di Jacob Klein (v., 1996; v. Klein e Luckham, 1984). Recentemente è stato affrontato il problema dell'energia necessaria a confinare tra pareti parallele sia singole catene che reticoli bi- e tridimensionali (v. Allegra e Raos, 2002).

b) Polimeri in massa

fig. 11

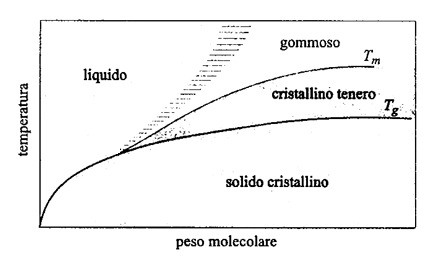
1. Gli stati viscoso e vetroso. - I polimeri possono presentarsi in molteplici stati fisici, e quindi con diverse proprietà, al variare della temperatura e del peso molecolare. Nella fig. 11 è rappresentato il diagramma di fase di un polimero con struttura stereochimica regolare, che può quindi cristallizzare: per alti pesi molecolari e a temperature crescenti si osservano in successione uno stato cristallino relativamente fragile, uno stato cristallino tenero e uno stato gommoso. Nel diagramma di fase di un polimero incapace di cristallizzare perché ha una struttura irregolare (come il comune polistirolo atattico da imballaggi), manca la curva che fornisce la temperatura di fusione T_m, e l'area sopra la curva T_g corrisponde a un materiale gommoso, quella sottostante a un solido vetroso amorfo (ciò vale anche per la porzione amorfa di un polimero semicristallino). A temperature abbastanza alte il polimero tende a fluire come un liquido, tanto più viscoso quanto più alto è il suo peso molecolare. Negli stati amorfi (vetroso, gommoso, viscoso) le catene sono di norma nello stato imperturbato e quindi, per alti pesi molecolari, la loro conformazione su grande scala è ben descritta da un cammino casuale. Questo risultato teorico è stato confermato da misure di scattering di neutroni, da cui risulta che il raggio di girazione quadratico medio 〈S²〉₀ segue un andamento in buon accordo con l'equazione (8).

fig. 12

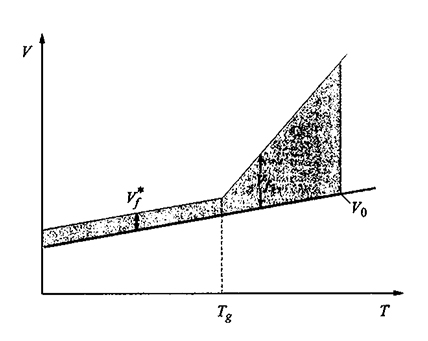
Lo stato vetroso è caratterizzato da una struttura così compatta da ostacolare fortemente lo spostamento relativo di molecole o di ampie porzioni di esse. Nel caso dei polimeri, nello stato vetroso sono generalmente consentite le rotazioni di gruppi laterali, ad esempio −CH₃, attorno al legame che li unisce alla catena, ma non i movimenti della catena principale. In tale stato esiste quindi un alto grado di cooperatività, perché ogni molecola o porzione di essa blocca lo spostamento delle circostanti, che a loro volta bloccano le vicine, e così via. Ne deriva un effetto a lungo raggio, e ci si potrebbe attendere che il passaggio dallo stato amorfo a quello vetroso sia una transizione del secondo ordine. In realtà, l'opinione prevalente è che tale transizione sia controllata da fattori cinetici e che non si tratti di una trasformazione di equilibrio; infatti, il valore della temperatura di transizione T_g risulta tanto più basso quanto più lento è l'esperimento che lo rileva. Diversi autori ritengono che, pur non essendo T_g una grandezza di equilibrio, debba esistere una temperatura di equilibrio T₂ - in linea di principio rilevabile con esperimenti estremamente lenti - definita come il limite inferiore di T_g. In particolare, con un importante teorema C. Austen Angell (v., 1970) ha dimostrato la necessità che esista la temperatura limite T₂, evitando la conclusione assurda (nota come 'paradosso di Kauzman') che alle basse temperature l'entropia dello stato vetroso sia inferiore a quella del cristallo. La descrizione più comunemente accettata per il passaggio vetro-amorfo nei polimeri è quella detta del volume libero, definito come la parte di volume che eccede il valore minimo V₀ consentito alla temperatura considerata; se il polimero è capace di cristallizzare, V₀ è identificabile col volume dello stato cristallino. Con riferimento al grafico sperimentale volume specifico-temperatura mostrato in fig. 12, si assume che il contributo del volume libero V_f sia costante per T 〈 T_g (= V_f*) e che esso vari linearmente come indicato in figura per T 〉 T_g. Passando al volume libero frazionario f = V_f/V₀, per T ≥ T_g si ha

formula  (20)

dove α_f è il coefficiente di espansione differenziale. Alla temperatura vetrosa T_g corrisponde dunque il minimo valore possibile del volume libero frazionario f_g. Benché sia T_g che f_g possano cambiare a loro volta con la velocità dell'esperimento, i loro valori vengono identificati con quelli ottenuti secondo procedure standard.

Gibbs e DiMarzio (v., 1958) per primi hanno collegato teoricamente la transizione vetrosa ideale (alla temperatura T₂) alle proprietà conformazionali di un polimero. Secondo questi autori si ha stato vetroso quando l'entropia effettiva del polimero si annulla; essa è data dal contributo entropico delle catene isolate allo stato imperturbato, diminuito dell'entropia di volume escluso, cioè dovuta a stati non realizzabili per sovrapposizione tra atomi. L'entropia di una catena isolata comprendente N legami è data da

formula  (21)

dove la funzione di partizione Z_N(T) è definita dalla (6). L'entropia di volume escluso è calcolata tramite le probabilità di campo medio (mean-field). Il volume libero f_g è importante perché riduce la sovrapposizione fra atomi e, quindi, l'entropia di volume escluso. I risultati appaiono in ragionevole accordo coi dati sperimentali.

fig. 14

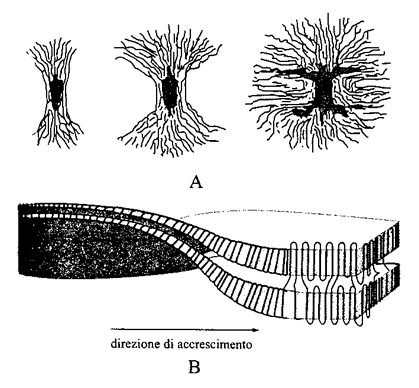
2. Lo stato cristallino. - Si possono distinguere due modalità di cristallizzazione di un polimero: cristallizzazione da massa fusa oppure da soluzione. Nel secondo caso, se la soluzione è molto diluita, si possono ottenere delle lamelle cristalline isolate il cui spessore è attorno ai 10 nm (v. fig. 13), mentre la larghezza può essere di diversi µm. Sorprendentemente, le catene polimeriche non sono orientate parallelamente al piano medio della lamella, ma sono all'incirca perpendicolari a esso. Se il polimero cristallizza da massa fusa, si ottengono lamelle strette e allungate, dette fibrille, che si aggregano in unità morfologiche più grandi (dell'ordine del µm; v. fig. 14), dette sferuliti. Le fibrille tendono a svilupparsi in direzione radiale e a deformarsi in senso elicoidale. È generalmente accettato che la struttura lamellare e il suo spessore siano da attribuire a fattori cinetici, poiché la struttura termodinamicamente più stabile dovrebbe essere quella di catene completamente estese. Lo spessore L delle lamelle ottenute a una temperatura T dipende da ΔT = T₀ - T, all'incirca come (ΔT)^-1; T₀ è la temperatura di fusione del cristallo ideale (v. fig. 15). Varie teorie sono state proposte per spiegare questa dipendenza, la più nota delle quali è quella dovuta a John D. Hoffman (v. Lauritzen e Hoffman, 1960; v. Hoffman, 1983). Secondo tale teoria, che si basa sul concetto di nucleazione secondaria superficiale, la formazione di una lamella è il risultato di una sequenza di eventi elementari, vale a dire la deposizione di un segmento della catena sulla superficie laterale. Detta l la lunghezza del segmento, la corrispondente variazione di energia libera ΔG_l può essere scritta come

ΔG_l  = σ - lΔg,   (22)

dove σ è l'energia libera associata al ripiegamento della catena dovuto alla deposizione di un segmento, e Δg è il valore dell'energia libera di fusione di un segmento di lunghezza unitaria; si ha Δg = Δh (T₀ - T)/T₀, dove Δh è l'entalpia di fusione. Se l è troppo piccolo, il ripiegamento è instabile perché ΔG_l è positivo. Il minimo valore di l (indicato con L) che consente la deposizione si ha quando ΔG_l = 0, e quindi

formula  (23)

fig. 16

Se si applica uno sforzo di trazione lungo le fibre di un polimero che cristallizza, si può ottenere una fibra cristallina orientata (v. fig. 16). Gli assi delle catene tendono a essere tutti paralleli alla direzione dello stiro, il che comporta un notevole aumento della resistenza meccanica del campione.

3. Lo stato liquido-cristallino. - È lo stato fisico in cui le catene sono tra loro parallele, ma la rotazione attorno al loro asse è sostanzialmente distribuita in modo casuale. Per vari polimeri lo stato liquido-cristallino può essere raggiunto entro un determinato intervallo di temperatura: a temperature inferiori a quelle nell'intervallo il polimero è cristallino, a temperature superiori è fuso. Si ritiene che questi polimeri possano essere ripartiti tra due classi-limite, l'una comprendente polimeri intrinsecamente rigidi, l'altra polimeri flessibili aventi un'elevata proporzione di gruppi laterali; questi ultimi sono i cosiddetti condis (per conformationally disordered) crystals (v. Wunderlich e Grebowicz, 1984; v. Wunderlich e altri, 1988), in cui la disposizione degli assi delle catene è spesso di tipo pseudo-esagonale e la cui struttura è probabilmente stabilizzata per ragioni entropiche. Il passaggio tra lo stato liquido-cristallino e quello fuso è generalmente quasi atermico, in accordo con la mancanza di interazioni specifiche fra le catene in entrambi gli stati.

fig. 17

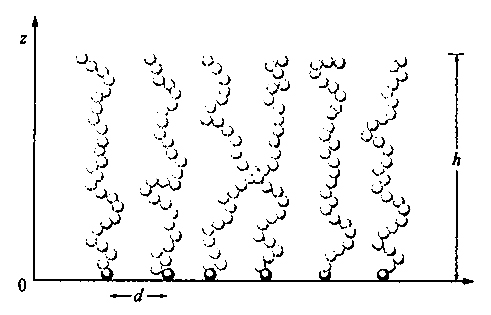
4. Polimeri vincolati a superfici. Copolimeri a blocchi. - La presenza di una superficie impenetrabile impone alla catena del polimero dei vincoli, di tipo sia entropico che energetico: se una catena flessibile si avvicina a una parete fino a distanze eguali o minori del suo raggio di girazione medio S̄, le possibili conformazioni si riducono di numero. Per minimizzare questa perdita entropica le catene più corte del polimero si disporranno a contatto della parete e, in una data catena, preferibilmente i gruppi terminali, che non impongono vincoli a segmenti successivi di catena. Se molte catene di eguale lunghezza sono aggraffate a una superficie con i loro terminali alla stessa distanza (v. fig. 17), l'energia libera di ognuna di esse è la somma dell'energia di volume escluso e dell'energia elastica. In unità k_BT, l'energia di volume escluso per catena è data da Nχ ∙ Φ, dove

è la frazione di volume occupato dalla catena stessa, N ed L sono il numero dei segmenti statistici e la loro lunghezza (v. eq. 7), h l'altezza delle catene e d la loro distanza. L'energia elastica dovuta alla lunghezza h della catena è invece proporzionale a

Minimizzando l'energia libera complessiva rispetto a h, si ha

formula  (24)

da cui si deduce che l'altezza h dello strato di polimero è direttamente proporzionale alla lunghezza di catena (N), invece che alla potenza N_3/5 come nella normale espansione dovuta al volume escluso. Si deve notare che anche in solvente ideale, dove le interazioni a due corpi sono compensate da quelle a tre corpi, che impongono la costanza del covolume, si ottiene la stessa dipendenza di h da N (v. Lodge e Muthukumar, 1996).

I copolimeri a blocchi sono caratterizzati da lunghe sequenze di unità A e B legate in modo covalente (del tipo ...−A−A−A−A−A−B−B−B−B−...). Assumendo che la temperatura sia sempre maggiore di quella di fusione di entrambi i polimeri, l'equilibrio del sistema è sempre raggiunto quando le unità A e B si separano in dominî distinti (microseparazione di fase). La ragione della separazione è legata a due ordini di considerazioni: a) la differenza tra l'energia di interazione fra unità diverse e_AB e la media tra unità eguali (e_AA + e_AB)/2 è sempre positiva (tranne il caso di interazioni di tipo ionico o fortemente polare, che qui non interessa); infatti si ha e_AB ∝ - √A • B, A, B〉 0 (v. Israelachvili, 1991²), e pertanto (v., per analogia, eq. 2)

formula (25)

e di conseguenza i contatti fra unità dissimili AB saranno ridotti al minimo; b) l'entropia di miscelazione tra le unità A e B tende a zero, in quanto l'entropia di mescolamento S_m tra le 'catene' è trascurabile perché il loro numero è relativamente piccolo. La separazione di fase, quindi, evita un costo energetico al prezzo di un trascurabile svantaggio entropico.

fig. 19

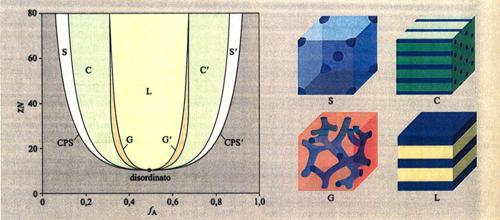
La dimensione tipica dei dominî è dell'ordine di 10 ÷ 100 nm. Nonostante entrambi i polimeri allo stato puro siano al di sopra della rispettiva temperatura di fusione, il sistema mantiene la sua stabilità macroscopica a causa dei legami chimici tra i microdominî (A) e (B); questi legami creano veri vincoli topologici (v. fig. 18). Perfino miscele di polimeri puri A_N e B_M possono essere rese compatibili dalla presenza del copolimero corrispondente. Studi teorici di campo medio autoconsistente sulla morfologia di copolimeri a due blocchi A_N - B_M hanno prodotto il diagramma di fase di fig. 19, dove i simboli S, C, G, L corrispondono, rispettivamente, alle strutture topologiche sferica, cilindrica, giroide, lamellare. La struttura giroide è un'interessante struttura bicontinua (entrambi i dominî sono connessi), ad alta simmetria, con curvatura media abbastanza piccola da permettere di ridurre la tensione interfacciale. La struttura giroide è molto frequente nei sistemi soffici condensati.

fig. 20

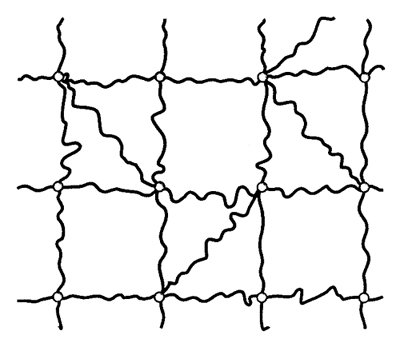
5. Reticoli polimerici. L'elasticità della gomma. - Come abbiamo visto nell'eq. (10), una lunga macromolecola agisce come una perfetta molla di richiamo sui suoi punti estremi. Un reticolo polimerico (v. fig. 20) è costituito da un insieme di catene macromolecolari allacciate tra loro da giunzioni, cioè da legami chimici permanenti, come nelle gomme ordinarie, o da associazioni dovute a interazioni polari o legami idrogeno (come nei gel; v. sopra, §2, punto 6). Come per la catena singola, l'elasticità del reticolo deriva dal fatto che lo stato indeformato ha entropia massima: ogni deformazione fa nascere una forza di richiamo che tende a riportare il sistema nel suo stato iniziale; le giunzioni garantiscono che si conservi la connessione tra le catene. Gli esperimenti condotti su campioni gommosi mostrano che la forza di richiamo è, con buona approssimazione, proporzionale alla temperatura assoluta T; ciò conferma la sua natura entropica ed è in accordo con l'ipotesi che la forza totale sia dovuta all'azione congiunta di forze entropiche delle singole catene. In realtà, l'estensione di un campione gommoso comporta un cambiamento delle conformazioni di catena anche su scala locale e, quindi, una variazione di energia. In particolare, nel caso di sequenze polietileniche (...−CH₂−CH₂−CH₂−...) la maggiore estensione ha come conseguenza un aumento delle rotazioni trans rispetto a quelle gauche, e quindi una diminuzione di energia (v. fig. 2); l'effetto che ne deriva è però generalmente trascurabile.

La teoria classica della gomma - elaborata principalmente da Werner Kuhn (v. Kuhn e Grün, 1942), da Hubert M. James e Eugene Guth (v., 1943) e da Flory (v. Flory e Rehner, 1943), nota come teoria KJGF dalle iniziali dei suoi autori - si fonda su un modello di reticolo costituito da catene fantasma (phantom network), cioè prive di volume e capaci di attraversarsi a vicenda mantenendo le reciproche connessioni. Un simile modello non riesce però a giustificare il volume proprio del campione gommoso. Si può infatti dimostrare che, per l'azione di contrazione dovuta alle catene, il sistema dovrebbe collassare a dimensioni simili a quelle occupate da una singola catena; invece gli esperimenti mostrano che il volume del campione è in accordo con quello deducibile dalla densità del polimero e si mantiene costante anche se sottoposto a deformazione, come è giusto attendersi per un polimero liquido. In un'elaborazione teorica più rigorosa, dovuta a James e Guth (v., 1943), si mantiene il volume vincolando un certo numero di giunzioni a essere fissate sulla superficie macroscopica del campione. L'energia libera elastica risulta essere:

formula  (26)

dove n è il numero delle catene (considerate tutte di eguale lunghezza e con entrambe le estremità collegate a giunzioni), r̄_m² la loro lunghezza quadratica media (lqm) nel campione indeformato e 〈r²〉₀ la corrispondente lqm nello stato imperturbato; (λ_x, λ_y, λ_z) sono i rapporti di deformazione lungo gli assi principali. Nel caso di deformazione monoassiale a volume costante si ha

,

e la forza

formula

esercitata sul campione è

formula, (27)

fig. 21

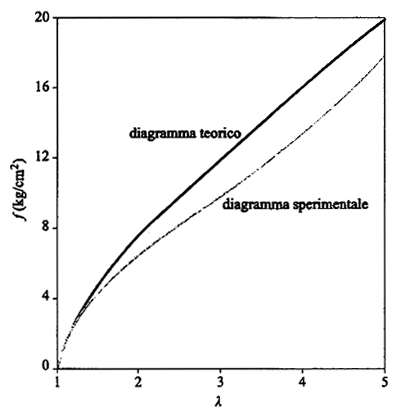
dove L₀ è la lunghezza iniziale del campione. La fig. 21 riporta un tipico diagramma sperimentale stress f (forza per unità di sezione) -λ (allungamento relativo) assieme alla curva dedotta dalla (27), riportata su scala opportuna. Per valori di λ superiori a 2 la curva sperimentale si abbassa rispetto a quella teorica (effetto Mooney). Esiste oggi un sostanziale accordo tra vari autori nell'individuare le cause di tale effetto nelle forze tra le catene che competono tra loro per riempire lo spazio; questa conclusione sembra confermata dall'osservazione che l'effetto Mooney tende a scomparire nel caso della gomma rigonfiata, cioè che ha assorbito molto solvente cosicché le catene non sono più a contatto diretto. In una interpretazione teorica di tale effetto (v. Ronca e Allegra, 1975) si propone che i valori medi delle fluttuazioni browniane delle giunzioni varino lungo gli assi x, y, z negli stessi rapporti esistenti tra λ_x, λ_y, λ_z (secondo la teoria James-Guth le fluttuazioni non sono influenzate dalla deformazione). In tal modo la probabilità di contatto tra i diversi segmenti delle catene non cambia in seguito alla deformazione e l'accordo con i dati sperimentali appare migliorare in modo sostanziale.

La teoria classica KJGF, riassunta, a meno di una modifica del fattore

,

dalla (27) è nota come 'teoria cinetica della gomma', in analogia alla teoria cinetica dei gas ideali in cui la pressione, corrispondente alla forza elastica, è legata all'energia cinetica delle molecole, pur essendo termodinamicamente di natura entropica. Anche le modifiche rese necessarie per spiegare l'effetto Mooney, o per mettere in conto il difficile problema degli entanglements fra le catene (v. Ball e altri, 1981; v. Edwards e Vilgis, 1986), non modificano la natura 'cinetica' della teoria. Tuttavia, le proprietà che si manifestano nello stato precedente la rottura del campione, note anche come 'proprietà ultime', non rientrano nella teoria classica, dato che in esse gioca un ruolo importante l'energia interna, oltre all'entropia. Queste proprietà danno luogo al tipico aumento della forza retrattile che si osserva in fig. 21 ad alti allungamenti (λ > 3,5 ÷ 4). Intervengono in questo caso due ordini di fenomeni che producono un aumento della forza retrattile, e cioè: 1) una parte delle catene si avvicina alla massima estensione, quindi la loro forza di richiamo è maggiore di quella lineare data dalla (10); 2) le catene molto allungate tendono a dar luogo a cristallizzazione secondo una morfologia a cristalli allungati in cui le ripiegature di catena tendono a scomparire, in contrasto con la classica morfologia lamellare di fig. 13. Ci limiteremo ad accennare solo al secondo aspetto, cioè la 'cristallizzazione sotto stiro', un fenomeno dovuto al fatto che l'entropia di fusione ΔS_f = S(liquido)-S(cristallo) diminuisce in condizioni di stiro perché le catene (liquide) molto estese hanno poca libertà conformazionale. Di conseguenza, sotto stiro la loro temperatura di fusione T_f = ΔH_f/ΔS_f è più grande della normale temperatura T_f⁰ e può superare la temperatura ambiente T_a. In conclusione, le catene possono cristallizzare se la loro normale temperatura T_f⁰ è abbastanza vicina a quella ambiente e lo stiro è abbastanza energico. Una prerogativa che rende più facile la cristallizzazione sotto stiro è l'esistenza di disordine allo stato cristallino del polimero; questo fa aumentare S(cristallo) e quindi fa diminuire ΔS_f a parità di deformazione. Tale disordine cristallografico è stato riscontrato proprio nella gomma naturale, cioè il poli(cis-1,4)isoprene (v. Corradini, 1975).

In generale, un buon polimero elastomerico deve essere cristallizzabile, avere una temperatura di fusione inferiore, ma non troppo, a quella ambiente e avere una temperatura vetrosa inferiore a quella di fusione (v. fig. 11).

3. Le proprietà dinamiche dei polimeri

fig. 22

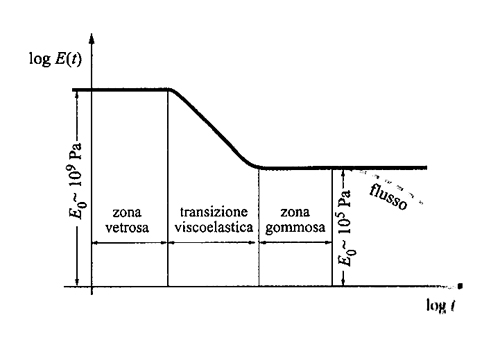
Tipicamente i polimeri hanno le caratteristiche proprie delle sostanze viscoelastiche: hanno cioè comportamento elastico se vengono sollecitate rapidamente, ma possono anche fluire lentamente come miele o sciroppo. È importante, per questi sistemi, definire la scala dei tempi di osservazione del fenomeno che si vuole analizzare. Esiste una correlazione tra la scala dei tempi e quella delle distanze: quanto più breve è il tempo di osservazione, tanto più localizzato è il fenomeno. Come già per le proprietà di equilibrio dei polimeri, anche in dinamica si può stabilire un principio di universalità: la fig. 22 mostra l'andamento del modulo dinamico in funzione del tempo t di osservazione, per temperature maggiori di T_g: tutti i polimeri amorfi sono vetrosi se osservati per tempi molto brevi, poi gradualmente diventano gommosi su tempi più lunghi, e infine fluiscono come liquidi viscosi (linea tratteggiata in figura). Almeno entro certi limiti lo stesso grafico vale a temperature diverse, salvo una traslazione lungo l'ascissa dei tempi in scala logaritmica (ovvero una moltiplicazione dei tempi per un fattore fisso). La presenza di cristallinità comporta modificazioni nella figura, in particolare non si ha in genere flusso in tempi lunghi; i polimeri cristallini, però, contengono sempre una porzione percentualmente rilevante di sostanza amorfa e quindi molti aspetti della fig. 22 continuano a essere validi anche in questo caso.

La dinamica dei polimeri in soluzione è diversa da quella nello stato 'di massa' cui si riferisce la fig. 22. In particolare, se la soluzione è diluita, i polimeri manifestano per alcuni aspetti un comportamento universale, ma mostrano anche importanti differenze, da considerarsi come espressioni della loro 'personalità'. Poiché lo studio delle soluzioni diluite è estremamente importante per la caratterizzazione molecolare dei polimeri, ne esamineremo subito alcuni aspetti rilevanti. Salvo contrario avviso ci riferiremo al comportamento newtoniano: le equazioni dinamiche sono lineari e, in particolare, la viscosità non dipende dal flusso. Tale comportamento corrisponde all'approssimazione perturbativa del primo ordine ed è effettivamente osservato per deboli campi di flusso, tali da non modificare le conformazioni medie delle macromolecole (v. Yamakawa, 1971; v. Doi ed Edwards, 1986).

a) Soluzioni diluite

1. Il modello Rouse-Zimm. - In analogia alla fig. 6, la catena è dinamicamente assimilata a un insieme di pseudo-atomi, o beads (grani), separati l'uno dall'altro da un numero di legami abbastanza alto che il segmento di catena corrispondente può essere considerato come una molla ideale (modello bead-and-spring). Ogni bead segue l'equazione di moto di Langevin ed è sottoposto alle seguenti forze: la forza elastica delle due molle che lo collegano alla catena; la forza viscosa, proporzionale alla velocità relativa rispetto al solvente; e la forza stocastica browniana (la forza inerziale è trascurabile). Si assume in genere che il solvente sia ideale.

Nella teoria di Prince E. Rouse (v., 1953) si assume inoltre che il moto della catena non perturbi la velocità del solvente. Le equazioni di moto per i beads possono essere disaccoppiate mediante diagonalizzazione di una semplice matrice simmetrica e si può scrivere l'equazione di Langevin per l'onda x~_k associata al k-esimo modo normale, (k = 1,2,..N - 1), che descrive il moto medio dei singoli atomi di catena:

formula  (28)

I tre termini corrispondono rispettivamente alla forza elastica, alla forza viscosa (ζ è il coefficiente di frizione col solvente) e alla forza browniana; se dall'esterno venisse impartito al solvente un flusso ν_x, alla (28) si dovrebbe aggiungere il termine - ζν_x. La coordinata normale x~_k(t) è definita da

formula, (29)

e rappresenta una modulazione sinusoidale della catena con k semi-onde. La costante di forza elastica K_k è data da

formula,  (30)

dove 〈x~_k²〉 è la media quadratica di x~_k(t) per t generico, in assenza di forze applicate. Bruno H. Zimm (v., 1956) tiene conto anche della perturbazione indotta dalla catena sul moto del solvente. Usando la teoria di Wilhelm Oseen secondo John G. Kirkwood (v., 1954), l'interazione con il solvente induce sull'atomo h-esimo una forza aggiuntiva pari, in approssimazione di quasi equilibrio, a

,

dove η_S è il coefficiente di viscosità del solvente puro, r_jh è la distanza fra gli atomi j e h, f_xj è la componente x della forza elastica agente sull'atomo j. Ne risulta un'equazione dinamica formalmente simile alla (28), ma con un coefficiente di frizione ζ dipendente dal modo k (ζ → ζ_k). Per una soluzione ideale e per N grande si ha

formula.   (31)

La (28) può essere integrata e x~_k(t) dipende dalla somma di effetti prodotti dalle forze browniane per tempi t′ 〈 t (integrale di memoria):

formula.   (32)

La seconda delle espressioni (32) esprime il teorema di fluttuazione-dissipazione, che lega le fluttuazioni della forza browniana alla temperatura e al coefficiente di frizione. Il tempo di rilassamento τ_k si ricava dalle eqq. (31) e (32) (assumendo C~_q ≈ C~_q=0 = C_∞) ed è dato, rispettivamente nelle due teorie, da

formula.  (33)

Sulla base sia di considerazioni teoriche, sia di conferme sperimentali il modello di Rouse risulta appropriato per catene abbastanza corte ( free-draining limit); nel caso di polimeri 'lunghi', invece, solo la teoria di Zimm riesce a riprodurre i risultati sperimentali, in cui è importante l'effetto di trascinamento del solvente da parte del gomitolo polimerico (non-draining limit).

Il coefficiente di frizione ζ è proporzionale alla viscosità del solvente η, e quindi dalla (33) segue, indicando con l'indice 0 uno stato di riferimento,

formula.  (34)

Se, al variare di η e di T, il tempo di osservazione varia in modo proporzionale ai tempi di rilassamento, cioè proporzionalmente ad a_T, si rivelano fenomeni dinamici simili. È questo l'importante principio di equivalenza tempo-temperatura: qualunque proprietà dinamica ottenuta alla temperatura T₀ può essere riportata alla temperatura T se il tempo di osservazione viene moltiplicato per a_T (e un'analoga correzione viene fatta alla proprietà stessa).

2. La viscosità complessa. - Ponendo la soluzione tra due piastre oscillanti in modo da applicare al solvente un moto periodico di taglio con frequenza ω, la viscosità presenta un termine in fase con la deformazione (componente viscosa) e uno sfasato di 90° (componente elastica). Le ampiezze dei due termini sono denominate rispettivamente η′(ω) e η′′(ω) (v. Ferry, 1970²) e la viscosità complessa è data da:

η(ω) = η′(ω) - iη"(ω).  (35)

Il modello Rouse-Zimm permette di ricavare dall'equazione di Langevin (28) l'espressione:

formula,   (36)

dove η_S è la viscosità del solvente, c ed m sono, rispettivamente, la concentrazione del polimero in g/l e la sua massa molare per atomo di catena, costituita da N atomi. Comunemente si usa il modulo complesso di rilassamento G(ω), dato da:

formula, (37)

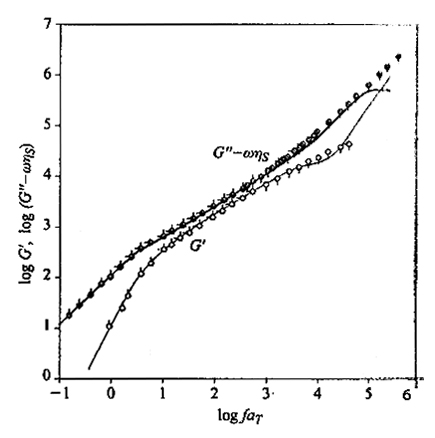
dove si sono introdotte le variabili ridotte τ′_k = t_k/t₁ e ω̄ = ωτ₁/2. La fig. 23 riporta in scala doppio-logaritmica i grafici di G′ e di G′′ - ωη_S in funzione di ω sia per il modello Rouse che per il modello Zimm. Per ωτ₁ 〈1 le curve di G′ e di G′′ hanno la loro massima pendenza (2 e 1, rispettivamente), pendenza che diminuisce abbastanza nettamente per ωτ₁>1. Infatti, nella prima zona viene attivato solo il modo normale con il massimo valore di τ, quindi G′∝ ω₂τ₁², G′′ -ωηS ∝ ωτ₁ (≪ 1); poiché ωτ_k ≪ ωτ₁ per ogni k > 1, il contributo di tutti gli altri modi è trascurabile. Va notato che questo è uno dei pochi casi in cui il contributo di un dato modo normale viene osservato separatamente dagli altri, dato che a frequenze maggiori si ha sempre sovrapposizione tra i contributi dei vari modi normali. A frequenze più alte (ωτ_N-1 ≅ 1) nel grafico si osserva una seconda discontinuità nelle pendenze; tuttavia bisogna osservare che i modi normali con k ≈ N, corrispondenti al moto localizzato di uno o pochissimi legami di catena, non possono essere trattati accuratamente in alcun modello lineare, come è quello di Rouse-Zimm.

Dalla (36) si può ricavare la viscosità limite η(0) per ω → 0. Questa importante grandezza è di solito espressa attraverso la viscosità intrinseca, definita come

formula;  (38)

dalle eqq. (33) e (36) si ottiene, ricordando che ζ∝ η,

formula,  (39)

dove l'esponente p vale 1 e 0,5 nei limiti di Rouse e di Zimm, rispettivamente. Nel secondo caso, che, come detto, ben descrive polimeri con pesi molecolari relativamente alti, con trascinamento del solvente all'interno del gomitolo polimerico, si può usare in alternativa l'equazione di Einstein per la viscosità prodotta da sfere galleggianti in soluzione:

formula,  (40)

dove R_η è il raggio idrodinamico (effettivo) della sfera, N_Avog è il numero di Avogadro. Poiché R_η è proporzionale alla radice quadratica media del raggio di girazione √ 〈S²〉₀ ∝ N^1/2l, l'ultima equazione è coerente con la (39), p = 1/2. L'equazione di Einstein predice inoltre l'esponente p nel caso di buon solvente: da R_η ∝ √ 〈S²〉 ∝ N^3/5l si ricava p = 0,8, in accordo con il risultato ottenibile da un esame più accurato della (39). Un parametro di significato analogo a R_η è rappresentato dal raggio idrodinamico R_H, che permette di ottenere il coefficiente di diffusione D della catena; si ha

formula. (41)

3. La rigidità locale; la viscosità interna. - Per sequenze di legami abbastanza corte, la catena imperturbata tende a non piegarsi; con riferimento alla fig. 5, questa rigidità conformazionale è tanto maggiore quanto più alto e stretto è il grafico della funzione C~_q nei pressi dell'origine: ciò dipende dalla correlazione statistica tra le rotazioni di catena, che determina un alto valore della lunghezza L ≅ C_∞l del segmento statistico, dove C_∞ = C~_q=0. Come si vede dalle (32), la rigidità conformazionale si riflette sul comportamento dinamico: i tempi di rilassamento τ_k tendono a essere particolarmente brevi per modi localizzati (k e q grandi); va notato che per la catena bead-and-spring ideale si ha invece C~_q = costante.

Un effetto dinamico più marcato sembra essere dovuto alla cosiddetta viscosità interna, causata dall'effetto dissipativo e frenante delle barriere di energia tra i minimi rotazionali (v. fig. 2). È stato proposto su basi teoriche (v. Allegra e Ganazzoli, 1981 e 1989) che la viscosità interna si traduca in un termine aggiuntivo al primo membro dell'equazione di Langevin (28), pari a

formula.  (42)

fig. 24

Il tempo τ₀ è il tempo caratteristico di ogni rotazione e Δ è l'energia di attivazione media del processo di rotazione. Il doppio segno presente nella (42) è connesso con le due possibili direzioni di propagazione delle onde di fluttuazione browniana, la cui velocità non può superare il valore di τ₀^-1 legami/s. La fig. 24 riporta dati sperimentali e calcolati di G′ e G′′ - ωη_S per soluzioni di polistirolo atattico in solventi altamente viscosi (Aroclor). Il valore di τ₀ è risultato pari a 1,9 • 10^-7 s (per T = 300 K); l'effetto della viscosità interna è desumibile per confronto con la fig. 23, nella zona delle alte frequenze.

Più recentemente il gruppo di Dieter Richter (v. Arbe e altri, 2001) ha condotto misure sistematiche di scattering quasi-elastico di neutroni per confrontare catene di eguale lunghezza di polidimetilsilossano (PDMS, un polimero con barriere rotazionali piccole o nulle) e poliisobutilene (PIB) in soluzioni di toluene, ottenendo una buona interpretazione quantitativa dei dati con

per il PIB e valore trascurabile per il PDMS. La barriera rotazionale risultante (Δ = 3,1 kcal/mol) è in buon accordo con il valore atteso, come anche il fattore pre-esponenziale, vicino al valore previsto dal metodo dello stato di transizione (v. Kramers, 1940). Il valore, molto grande, di τ₀ ottenuto per il polistirolo in soluzioni di Aroclor può essere giustificato dall'alta viscosità del solvente (≅ 2,5 P a 300 K contro ≅ 0,4 cP per il toluene), in accordo con la teoria di Hendrik A. Kramers nel limite di alte viscosità. È da rilevare che, quando interviene la viscosità interna, il principio di equivalenza tempo-temperatura non è più valido nella forma semplice della (34), dato che viene introdotta una nuova dipendenza τ₀/temperatura secondo la formula di Arrhenius (v. eq. 42).

4. Lo scattering dinamico. - Lo scattering subito da fasci di fotoni, o di particelle subatomiche come elettroni o neutroni, è caratterizzato da un effetto Doppler dovuto alla velocità delle molecole che diffondono la radiazione (scattering quasi-elastico, o dinamico). L'intensità della radiazione diffusa è data dal S(Q,t):

formula,  (43)

dove R_i(t) è il vettore posizione dell'atomo di catena i al tempo t, Q il vettore di scattering (Q = |Q| = 4 πsin(θ/2)/λ, θ e λ sono rispettivamente l'angolo di deflessione della radiazione e la sua lunghezza d'onda). Si dimostra che

formula,  (44)

dove il primo termine al secondo membro è legato alla diffusione del baricentro della catena (v. eq. 41), mentre il secondo corrisponde al moto degli atomi a baricentro fisso e ha un valore limite finito

formula.

fig. 25

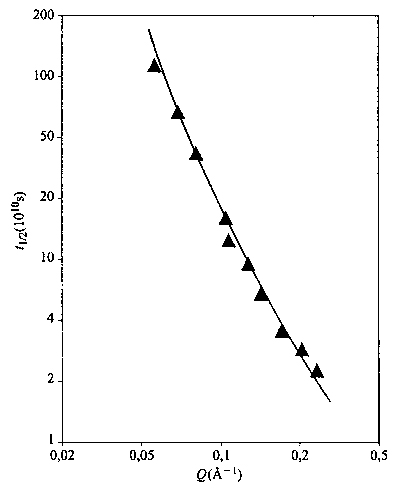
La funzione S(Q,t) diminuisce all'aumentare del tempo t e, per differenti valori di Q, misura tipi diversi di movimento. Per Q piccolo sono osservate lunghe distanze, quindi S(Q,t) è soprattutto influenzata dai modi collettivi (piccoli k) e dalla diffusione; se invece Q〈S²〉^1/2 ≫ 1 sono in gioco i moti più localizzati e più veloci. La fig. 25 mostra come varia il tempo di dimezzamento t_1/2 di S(Q,t) al variare di Q nel caso di polistirolo atattico. Rappresentando, come d'uso, questa funzione con la legge di potenza approssimata t_1/2Q^β ≅ costante, l'esponente β vale 2 per Q〈S²〉^1/2 〈 1 (diffusione) e cresce a valori maggiori per Q〈S²〉^1/2 〉 1. Per catene flessibili, come ad esempio il polidimetilsilossano, l'esponente assume valori anche superiori a 3, mentre per catene relativamente rigide come il polistirolo e il PIB non viene superato il valore di 2 (v. Allegra e altri, 1984). A sua volta, la rigidezza può essere sia di equilibrio (cioè dovuta a un massimo alto e stretto, nell'origine del grafico di C~_q; v. fig. 5), oppure di tipo dinamico, legata alla viscosità interna; almeno nel caso del PIB il secondo fattore pare essere nettamente prevalente (v. Arbe e altri, 2001).

b) Polimeri fusi e soluzioni concentrate

1. Polimeri fusi. - Nel precedente paragrafo a), punto 3, si è già accennato al fatto che in un polimero fuso ogni catena di N legami si trova nello stato imperturbato e ciò ne semplifica la statistica conformazionale: sappiamo, ad esempio, che il suo raggio quadratico medio di girazione 〈S²₀〉 è pari a NC_∞l²/6 (v. eq. 8). Le proprietà dinamiche sono invece più complesse.

Se la lunghezza N di catena è inferiore a un certo limite N_c, la viscosità del polimero obbedisce piuttosto bene alla (39), con p = 1, cioè [η] ∝ η ∝ N, in accordo con il modello di Rouse che ne interpreta anche la diffusione. Il moto della catena non si accompagna a interazione idrodinamica e la catena non incontra ostacoli diversi dal normale attrito con il mezzo circostante. Se invece si ha N ≫ N_c, allora si ottiene η ∝ N^3,4. L'interpretazione più accettata di questa discontinuità è data dalla cosiddetta 'teoria della reptation' (v. fig. 26; v. de Gennes, 1979; v. Doi ed Edwards, 1986). La catena non può diffondere liberamente perché esistono molti punti di allacciamento (entanglements) con le catene circostanti; solo quando la catena è più corta della lunghezza compresa tra due successivi allacciamenti essa può muoversi liberamente secondo il modello di Rouse. Come indica la fig. 26, il solo modo di diffusione permesso alla catena consiste nello 'sbucar fuori' come un rettile dal tubo in cui è contenuta; in tal modo il tubo è gradatamente distrutto e la catena cambia posizione. Si definisce tempo caratteristico di reptation, τ_rep, il tempo medio necessario alla catena per uscire completamente dal tubo iniziale. Poiché il coefficiente d'attrito è proporzionale a N e l'ampiezza quadratica media 〈x~_k²〉^1/2 è proporzionale alla lunghezza Nl della catena (in quanto il movimento avviene solo secondo l'asse del tubo), dalla (32) si ottiene:

τ_rep ∝ N³/T,   (45)

e si può dimostrare che η ∝ τ_rep. La differenza rispetto al valore sperimentale dell'esponente (~ 3,4) è significativa e va probabilmente attribuita alle seguenti inadeguatezze della teoria: 1) il modello della reptation assume che una sola catena alla volta si muova nel campo medio generato da tutte le altre catene; 2) il modello non dice nulla sulla reale natura degli allacciamenti, assumendo semplicemente che esistano; 3) il movimento di tipo reptation è un assunto a priori, non il risultato di una teoria microscopica. Tuttavia, si può ritenere che tale modello descriva l'essenza dei fenomeni complessi riguardanti la dinamica di un polimero fuso, anche se ulteriori approfondimenti potranno essere utili.

2. L'equivalenza tempo/temperatura: la legge di Williams-Laendel-Ferry. - Come nel caso delle soluzioni, è utile estrapolare dati sperimentali e/o teorici a tempi o velocità diverse da quelle sotto analisi modificando solo la temperatura. Per i polimeri fusi il punto di partenza è la legge di Doolittle per le viscosità dei liquidi ordinari. Arthur K. Doolittle ha trovato una corrispondenza, sostanzialmente generale, tra la viscosità η e il volume libero frazionario f = f_g + α_f(T - T_g) (v. eq. 20)

formula,  (46)

dove A e B sono due costanti empiriche. Considerando la connessione tra viscosità e tempi di rilassamento, questa legge è stata applicata al generico valore di τ_k(T) dei polimeri allo stato liquido (T 〉 T_g), ottenendo:

formula,  (47)

cioè il fattore di traslazione in scala logaritmica per l'asse dei tempi in modo da ricavare una curva maestra: risultati ottenuti sugli stessi campioni a temperature diverse, in intervalli di tempi (o di frequenze) uguali, permettono per confronto di ricavare il valore dei tempi nella giusta scala. Il riferimento alla temperatura vetrosa T_g appare naturale se si pensa che essa rappresenta una singolarità dinamica per tutte le sostanze. La (47) è l'equazione di Williams, Laendel e Ferry (WLF), il cui largo impiego è giustificato tra l'altro dal fatto che i parametri f_g, α_f e B sono costanti valide per tutti i polimeri, le prime due avendo lo stesso valore per polimeri diversi entro limiti assai ristretti (v. Ferry, 1970²).

3. Le soluzioni concentrate. - Si dicono concentrate le soluzioni per le quali la concentrazione c del polimero supera il valore c* che corrisponde al contatto stretto fra tutti i gomitoli polimerici (v. eq. 4). In questo caso la descrizione dinamica delle catene è più complicata. Per valori crescenti di c si ha una progressiva soppressione (screening), da parte delle catene circostanti, sia dell'interazione idrodinamica, sia dell'effetto di volume escluso, con contrazione progressiva delle dimensioni di catena. Per c crescente, inoltre, aumenta progressivamente il numero degli allacciamenti e il meccanismo dinamico della reptation si completa all'incirca per c compreso tra 2 c* e 10 c*. Inoltre, il coefficiente di frizione risulta essere una funzione molto rapidamente crescente con la concentrazione, particolarmente per polimeri aventi la temperatura T_g al di sopra di quella ambiente, come ad esempio il polistirolo. È questo un campo in cui l'interpretazione dei dati appare particolarmente controversa; dovranno quindi essere individuati strumenti teorici più adeguati.

4. Prospettive future

I polimeri offrono grandi opportunità per lo studio chimico-fisico della materia 'soffice' condensata, poiché è possibile variarne, entro ampi limiti, sia il peso molecolare, sia la struttura stereochimica. In particolare, le forze intermolecolari possono essere variate con molta accuratezza controllando i due fattori suddetti; si aprono così importanti prospettive, ad esempio per studi di autoorganizzazione e di transizioni di fase. A causa della lunghezza delle catene e del disordine statistico che generalmente ne deriva, i polimeri possono essere studiati teoricamente con metodi di campo medio, che permettono anche l'applicazione diretta delle trasformazioni di scala a molti problemi. Le normali scale di lunghezza si prestano bene all'analisi quantitativa mediante scattering (di raggi X, neutroni, elettroni, ecc.) e, in misura sempre crescente, mediante microscopia. Sul piano dinamico, la grande estensione delle scale dei tempi di rilassamento, tipica dei polimeri, permette di seguire complessi fenomeni cinetici in grande dettaglio. La temperatura vetrosa ha generalmente valori abbastanza alti da permettere di congelare eventuali microstrutture di interesse mediante rapido raffreddamento. Le dimensioni caratteristiche dei dominî polimerici - quali si incontrano nelle miscele polimeriche e nei copolimeri a blocchi, nei polimeri semicristallini e liquido-cristallini - sono generalmente comprese tra 1 e 100 nm, collocandosi a mezza via tra le distanze di interesse nella cristallografia chimica (0,1 ÷ 1 nm) e le dimensioni tipiche dei grani cristallini di molte sostanze (100 ÷ 1.000 nm). La formazione delle morfologie polimeriche è controllata da un delicato intreccio di fattori termodinamici e cinetici che rappresenta una sfida importante per l'analisi teorica.

Molte applicazioni dei polimeri sono connesse a fenomeni interfacciali; basti pensare agli adesivi, alle vernici e ai surfattanti; la comprensione a livello molecolare di tali fenomeni è progredita solo in tempi recenti. Anche i copolimeri a blocchi costituiscono un esempio per tali applicazioni, data l'importanza delle superfici di separazione tra i dominî. Va tenuto presente che, a causa delle dimensioni molecolari, lo spessore degli strati polimerici perpendicolari alla superficie è dell'ordine di alcune decine di nm; pertanto, la struttura del polimero riflette essenzialmente proprietà di massa, che tuttavia sono influenzate dalla presenza della superficie. Mentre appaiono relativamente accessibili le caratteristiche strutturali lungo la direzione perpendicolare alla superficie, poco si conosce della struttura proiettata sulla superficie stessa. La conoscenza e il controllo di tale struttura potrebbero aprire nuove strade alla chimica-fisica macromolecolare, ad esempio verso la preparazione e lo studio di membrane sintetiche. A questo punto è bene ricordare la rapida diffusione della simulazione al calcolatore, soprattutto mediante dinamica molecolare, che si manifesta sempre più efficacemente come una terza metodologia di ricerca, accanto agli esperimenti e alla teoria. Fenomeni non osservabili in pratica perché la loro scala delle distanze o dei tempi è troppo piccola possono essere 'osservati' mediante la simulazione.

Effetti dinamici importanti e delicati accadono all'interfaccia tra polimeri reticolati (gomme) e superfici rigide. Tra questi il molto discusso effetto Payne, ovvero il forte aumento del modulo G′ al diminuire dell'ampiezza di deformazione, per una data frequenza del moto relativo tra polimero e superficie. Sia il comportamento elastico che, ancor più, quello dissipativo, sono influenzati da questi fenomeni interfacciali. Effetti ancora più marcati sembrano interessare polimeri non reticolati a contatto di superfici. È questo un campo in cui oggi la viscoelasticità e la termodinamica di non equilibrio si trovano a fronteggiare sfide importanti.

Va ricordata infine l'affinità strutturale, e potenzialmente anche funzionale, tra i polimeri sintetici e le macromolecole biologiche, come le proteine e gli acidi nucleici. I sistemi biologici possono fornire risposte forti a stimoli relativamente deboli attraverso un delicato equilibrio di differenti interazioni, quali legami idrogeno, interazioni idrofobico-idrofiliche, funzioni acido-base, ecc., mentre i normali polimeri sintetici hanno di regola una o poche interazioni caratteristiche. Lo sviluppo sintetico di strutture polimeriche e copolimeriche più sofisticate permetterà, tramite l'impiego di materiali sintetici 'soffici' come ad esempio i gel o i cristalli liquidi, di emulare il comportamento delle controparti biologiche, col vantaggio di una potenziale superiore efficienza.

Bibliografia

Allegra, G., Colombo, E., Polymer chains with excluded volume: critical exponents from free energy optimisation, in "The journal of chemical physics", 1994, CI, pp. 4268-4276.

Allegra, G., Colombo, E., Polymer chain in a good solvent between attracting walls. A scaling approach, in "The journal of chemical physics", 1996, CV, pp. 3801-3812.

Allegra, G., Ganazzoli, F., Configurations and dynamics of real chains: internal viscosity, in "Macromolecules", 1981, XIV, pp. 1110-1119.

Allegra, G., Ganazzoli, F., Chain configurations and dynamics in the Gaussian approximation, in "Advances in chemical physics", 1989, LXXV, pp. 265-348.

Allegra, G., Ganazzoli, F., Raos, G., The collapse of macromolecules in poor solvents, in "Trends in polymer science", 1996, IV, pp. 293-298.

Allegra, G., Immirzi, A., Neighbour interaction and internal rotation in polymers. A new classical approach to account for all rotational states, in "Makromolekulare Chemie", 1969, CXXIV, pp. 70-83.

Allegra, G., Raos, G., Confined polymer networks: the harmonic approach, in "The journal of chemical physics", 2002, CXVI, pp. 3109-3118.

Allegra, G. e altri, Dynamics of atactic polystyrene in solution, in "Macromolecules", 1984, XVII, pp. 1253-1263.

Angell, C. A., The data gap in solution chemistry. The ideal glass transition puzzle, in "Journal of chemical education", 1970, XLVII, pp. 583-587.

Arbe, A. e altri, Origin of internal viscosity effects in flexible polymers: a comparative neutron spin-echo and light-scattering study on poly(dimethylsiloxane) and poly(isobutylene), in "Macromolecules", 2001, XXXIV, pp. 1281-1290.

Ball, R. C., Doi, M., Edwards, S. F., Warner, M., Elasticity of entangled networks, in "Polymer", 1981, XXII, pp. 1010-1018.

Baumgärtner, A., Muthukumar, M., A trapped polymer chain in random porous media, in "The journal of chemical physics", 1987, LXXXVII, pp. 3082-3088.

Brückner, S., Allegra, G., Pegoraro, M., La Mantia, F. P., Scienza e tecnologia dei materiali polimerici, Napoli: EdiSES, 2001.

Casassa, E. F., Equilibrium distribution of flexible polymer chains between a macroscopic solution phase and small voids, in "Polymer letters", 1967, V, pp. 773-778.

Cherayil, B. J., Douglas, J. F., Freed, K. F., Effect of residual interactions on polymer properties near the theta point, in "The journal of chemical physics", 1987, LXXXVII, pp. 3089-3098.

Chu, B., Wang, Z., An extended universal coexistence curve for polymer solutions, in "Macromolecules", 1988, XXI, pp. 2283-2286.

Chu, B., Xu, R., Zuo, J., Transition of polystyrene in cyclohexane from the Θ to the collapsed state, in "Macromolecules", 1988, XXI, pp. 273-274.

Chu, B., Ying, Q., Grosberg, A. Y., Two-stage kinetics of single chain collapse. Polystyrene in cyclohexane, in "Macromolecules", 1995, XXVIII, pp. 180-189.

Cloizeaux, J. des, Jannink, G., Les polymères en solution: leur modélisation et leur structure, Les Ulis: Les éditions de physique, 1987.

Corradini, P., Conformation of polymer molecules and entropy of melting, in "Journal of polymer science. Polymer symposia", 1975, L, pp. 327-330.

Corradini, P., Nicolais, L., Materiali polimerici, in Enciclopedia del Novecento, vol. VIII, Supplemento, Roma: Istituto della Enciclopedia Italiana, 1989, pp. 673-688.

Corradini, P., Porri, L., Polimeri, in Enciclopedia del Novecento, vol. V, Roma: Istituto della Enciclopedia Italiana, 1980, pp. 423-451.

DiMarzio, E. A., Proper accounting of conformations of a polymer near a surface, in "The journal of chemical physics", 1965, XLII, pp. 2101-2106.

DiMarzio, E. A., Rubin, R. J., Adsorption of a chain polymer between two plates, in "The journal of chemical physics", 1971, LV, pp. 4318-4336.

Doi, M., Edwards, S. F., The theory of polymer dynamics, Oxford: Oxford University Press, 1986.

Domb, C., Gillis, J., Wilmers, G., On the shape and configuration of polymer molecules, in "Proceedings of the Physical Society", 1965, LXXXV, pp. 625-645.

Edwards, S. F., Vilgis, T., The effect of entanglements in rubber elasticity, in "Polymer", 1986, XXVII, pp. 483-492.

Ferry, J. D., Viscoelastic properties of polymers, New York: John Wiley & Sons, 1970².

Flory, P. J., The configurations of real polymer chains, in "The journal of chemical physics", 1949, XVII, pp. 303-310.

Flory, P. J., Principles of polymer chemistry, Ithaca, N. Y.: Cornell University Press, 1953.

Flory, P. J., Configurational statistics of chain molecules with interdependent rotational potentials, in Statistical mechanics of chain molecules, New York: Interscience, 1969, pp. 49-94.

Flory, J. P., Rehner, J. Jr., Statistical mechanics of cross-linked polymer networks, in "The journal of chemical physics", 1943, XI, pp. 512-526.

Freed, K., Renormalisation group theory of macromolecules, New York: Wiley, 1987.

Ganazzoli, F., La Ferla, R., Allegra, G., Kinetics of contraction of a stiff chain, in "Macromolecules", 1995, XXVIII, pp. 5285-5293.

Gennes, P.-G. de, Scaling concepts in polymer physics, Ithaca, N. Y.-London: Cornell University Press, 1979.

Gennes, P.-G. de, Kinetics of collapse for a flexible coil, in "Journal de physique. Lettres", 1985, XLVI, pp. L639-L642.

Gibbs, J. H., DiMarzio, E. A., Nature of the glass transition and the glassy state, in "The journal of chemical physics", 1958, XXVIII, pp. 373-383.

Grosberg, A. Y., Khokhlov, A. R., Statistical physics of macromolecules (1989), New York: American Institute of Physics, 1994.

Grosberg, A. Y., Nechaev, S. K., Shakhnovic, E. I., The role of topological constraints in the kinetics of collapse of macromolecules, in "Journal de physique", 1988, XLIX, pp. 2095-2100.

Hoffman, J. D., Regime III crystallization in melt-crystallized polymers. The variable cluster model of chain folding, in "Polymer", 1983, XXIV, pp. 3-26.

Israelachvili, J., Intermolecular and surface forces, London: Academic Press, 1991².

James, H. M., Statistical properties of networks of flexible chains, in "The journal of chemical physics", 1947, XV, pp. 651-668.

James, H. M., Guth, E., Theory of the elastic properties of rubber, in "The journal of chemical physics", 1943, XI, pp. 455-481.

Kirkwood, J. G., The general theory of irreversible processes in solutions of macromolecules, in "Journal of polymer science", 1954, XII, pp. 1-14.

Klein, J., Shear, friction and lubrication forces between polymer-bearing surface, in "Annual review of materials science", 1996, XXVI, pp. 581-612.

Klein, J., Luckham, P. F., Long-range attractive forces in an aqueous polymer solution, in "Nature", 1984, CCCVIII, pp. 836-837.

Kramers, H. A., Brownian motion in a field of force and the diffusion model of chemical reactions, in "Physica", 1940, VII, pp. 284-304.

Kuhn, W., Grün, F., Beziehungen zwischen elastischen Konstanten und Dehnungsdoppelbrechung hochelasticher Stoffe, in "Kolloid-Zeitschfrift", 1942, CI, pp. 248-271.

Landau, L. D., Lifshitz, E. M., Statistical physics, London: Pergamon Press, 1958.

Lauritzen, J. I. Jr., Hoffman, J. D., Theory of formation of polymer crystals with folded chains in dilute solution, in "Journal of research of the National Bureau of Standards (Section A)", 1960, LXIV, pp. 73-102.

Le Guillou, J.-C., Zinn-Justin, J., Accurate critical exponents from the epsilon-expansion, in "Journal de physique. Lettres", 1985, XLVI, pp. L137-L141.

Lifson, S., Neighbor interactions and internal rotations in polymer molecules, in "The journal of chemical physics", 1959, XXX, pp. 964-967.

Lodge, T. P., Muthukumar, M., Physical chemistry of polymers: entropy, interactions and dynamics, in "Journal of physical chemistry", 1996, C, pp. 13275-13292.

Raos, G., Allegra, G., A cluster of chains can be smaller than a single chain, in "Macromolecules", 1996, XXIX, pp. 8565-8567.

Ronca, G., Allegra, G., An approach to rubber elasticity with internal constraints, in "The journal of chemical physics", 1975, LXIII, pp. 4990-4997.

Rouse, P. E., A theory of the linear viscoelastic properties in dilute solutions of coiling polymers, in "The journal of chemical physics", 1953, XXI, pp. 1272-1280.

Scheutjens, J. M. H. M., Fleer, G. J., Statistical theory of the adsorption of interacting chain molecules, 1. Partition function, segment density distribution and adsorption isotherms, in "The journal of physical chemistry", 1979, LXXXIII, pp. 1619-1635.

Scheutjens, J. M. H. M., Fleer, G. J., Statistical theory of the adsorption of interacting chain molecules, 2. Train, loop and tail size distribution, in "The journal of physical chemistry", 1980, LXXXIV, pp. 178-190.

Wang, S.-Q., Douglas, J. F., Freed, K. F., Influence of variable draining and excluded volume on hydrodynamic radius with Kirkwood-Riseman model: dynamical renormalization group description to order ε², in "The journal of chemical physics", 1987, LXXXVII, pp. 1346-1354.

Wilson, K., Kogut, J., The renormalization group and the e-expansion, in "Physics reports", 1974, XII, pp. 77-199.

Wunderlich, B., Grebowicz, J., Thermotropic mesophases and mesophase transitions of linear, flexible macromolecules, in "Advances in polymer science", 1984, LX, pp. 1-59.

Wunderlich, B., Möller, M., Grebowicz, J., Baur, H., Conformational motion and disorder in low and high molecular mass crystals, in "Advances in polymer science", 1988, LXXXVII, pp. 1-121.

Yamakawa, H., Modern theory of polymer solutions, New York: Harper & Row, 1971.

Zimm, B. H., Dynamics of polymer molecules in dilute solution: viscoelasticity, flow birefringence and dielectric loss, in "The journal of chemical physics", 1956, XXIV, pp. 269-278.