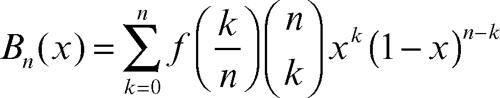Bernstein, polinomi di

Enciclopedia della Matematica (2013)

Bernstein, polinomi di


Bernštein, polinomi di in analisi, particolari polinomi che approssimano una funzione continua in un intervallo. Più precisamente, data una funzione ƒ(x) definita nell’intervallo [0, 1], i polinomi di Bernštein relativi a tale funzione sono i polinomi

formula

dove

formula

è il coefficiente binomiale.

Il teorema di Bernštein assicura che se ƒ è continua in [0, 1], allora la successione {Bn(x)} converge uniformemente a ƒ (x) in [0, 1]; lo scarto |ƒ(x) − Bn(x)| può quindi essere reso arbitrariamente piccolo, per qualunque scelta di x nell’intervallo, a patto di prendere n sufficientemente grande. Il teorema fornisce perciò una prova diretta e costruttiva del teorema di approssimazione polinomiale di → Weierstrass.

Vedi anche
approssimazione In matematica, si chiamano metodi, o procedimenti di a. o, semplicemente, a., procedure alle quali si ricorre per rappresentare enti matematici (numeri, misure, funzioni ecc.) in modo non esatto, ma sufficientemente accurato per gli scopi perseguiti, in genere mediante enti più semplici. Così, per es., ... numeri complessi Si chiama c. ogni numero della forma a + i b, essendo a e b due numeri reali relativi (positivi, negativi o anche nulli) e rappresentando il simbolo i (unità immaginaria o immaginario) la radice quadrata di −1; l’addendo a si chiama la parte reale, l’addendo i b la parte immaginaria, b il coefficiente ... matrice Anatomia Ammasso di cellule epiteliali alla cui attività si deve la formazione di un tessuto. M. dell’unghia L’ammasso di cellule dello strato onicogeno che si osserva in corrispondenza della radice dell’unghia e della lunula, e alla cui opacità è dovuto il colorito biancastro di quest’ultima. M. del ... numero reale Ogni numero relativo razionale o irrazionale. I numeri r. sono dati, perciò, da tutti i possibili sviluppi decimali sia limitati sia illimitati, e questi ultimi sia periodici sia sprovvisti di periodo. Due differenti ordini di problemi suggerirono ai matematici l’opportunità di introdurre i numeri reali. ...
Tag
Altri risultati per Bernstein, polinomi di
  • polinomio
    Enciclopedia on line
    In matematica, somma di monomi (in senso proprio, solo con riferimento a monomi interi), detti termini del p.: binomio, trinomio, quadrinomio ecc., è un polinomio rispettivamente di 2, 3, 4 ecc. termini; coefficienti di un p. sono i coefficienti dei suoi monomi; grado di un p. rispetto a una lettera ...
  • riduzione polinomiale
    Enciclopedia della Scienza e della Tecnica (2008)
    Fabrizio Luccio Nello studio della complessità di algoritmi combinatori l’attenzione è focalizzata sulla classificazione dei problemi come polinomiali o esponenziali. L’esame si può limitare alla versione decisionale che è il nucleo di complessità di un problema e si propone di stabilire se il dato ...
  • polinomio
    Dizionario delle Scienze Fisiche (1996)
    polinòmio [Comp. di poli- e -nomio di binomio] [ANM] Somma di più monomi, detti termini del p., i cui coefficienti sono detti coefficienti del p.; grado di un p. rispetto a una variabile è il grado massimo dei monomi rispetto a tale variabile e grado complessivo è il grado massimo dei monomi rispetto ...
  • POLINOMIO
    Enciclopedia Italiana (1935)
    Giovanni Lampariello . Termine in uso nell'algebra per indicare la somma di due o più monomî (v. monomio), che non siano tutti simili tra loro. Se dopo aver fatto la riduzione degli eventuali termini simili, il polinomio comprende due o tre termini, esso si chiama rispettivamente binomio o trinomio. ...
Vocabolario
polinòmio
polinomio polinòmio s. m. [comp. di poli- e -nomio di binomio]. – In matematica, somma di monomî (in senso proprio, solo con riferimento a monomî interi), detti termini del polinomio: binomio, trinomio, quadrinomio, ecc., è un polinomio...
Disforia di genere
disforia di genere loc. s.le f. Condizione di intensa e persistente sofferenza causata dal sentire la propria identità di genere diversa dal proprio sesso anatomico. ♦ «Come ha appena detto la compagna transgender...». I delegati di fabbrica...