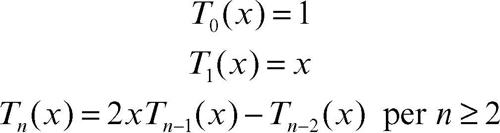Cebysev, polinomi di
Cebysev, polinomi di
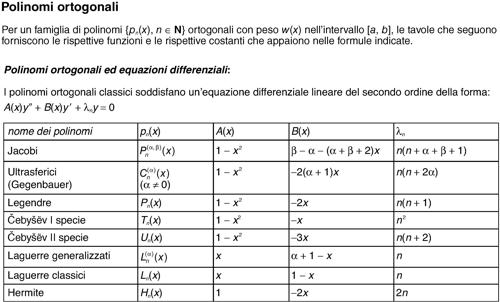
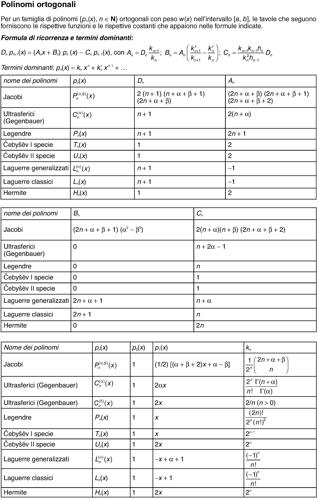
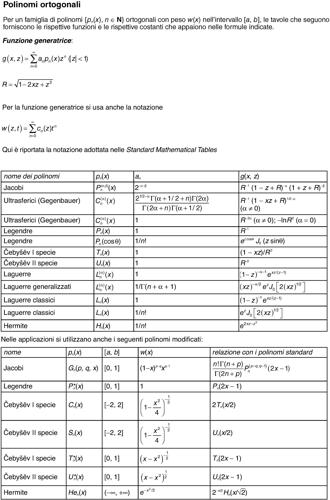
Čebyšëv, polinomi di (di prima specie) polinomi ortogonali nell’intervallo [−1, 1] rispetto alla funzione peso w(x) = (1 − x 2)−1/2 così definiti ricorsivamente:
Tali polinomi sono anche esprimibili in modo più semplice mediante la formula
e assumono in [−1, 1] il massimo valore assoluto più piccolo tra tutti i polinomi di pari grado. Pertanto, per ogni fissato grado n, il polinomio che meglio approssima una funzione nella norma C0([−1, 1]) è il polinomio interpolatore negli zeri di Tn(x), che sono i punti
Questa caratteristica spiega l’importanza che i polinomi di Čebyšëv occupano nell’ambito della teoria dell’approssimazione e, in particolare nella interpolazione polinomiale di una funzione mediante n + 1 punti nell’intervallo [−1,1], rendendo minimo l’errore di interpolazione se i punti scelti sono gli zeri del (n + 1)-esimo polinomio di Čebyšëv.
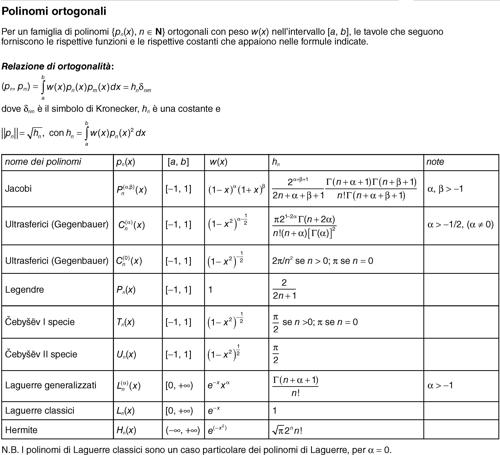
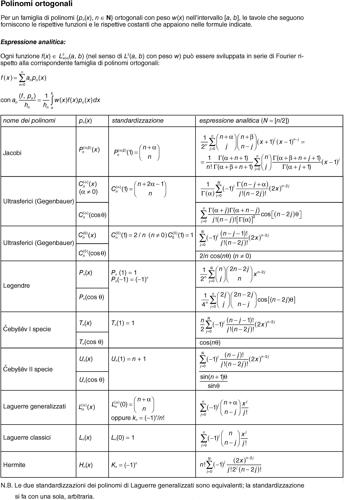
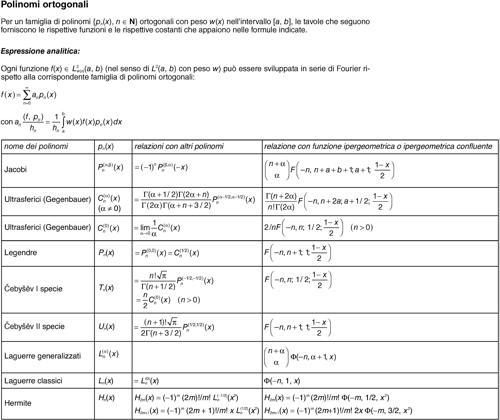
Per i polinomi di Čebyšëv (anche di seconda specie) si vedano le relative tavole.