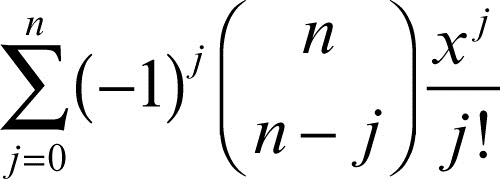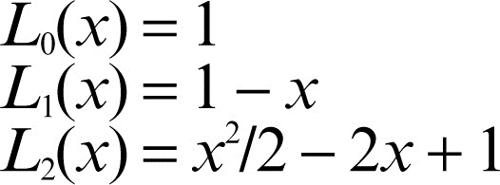Laguerre, polinomi di
Laguerre, polinomi di
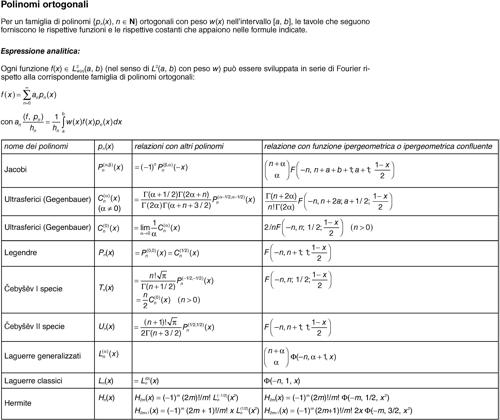
Laguerre, polinomi di espressi come
con α > −1, sono polinomi ortogonali sulla semiretta [0, +∞) rispetto alla funzione peso x αe−x (nel caso generalizzato, nel caso classico α = 0; si vedano le tavole dei polinomi ortogonali).
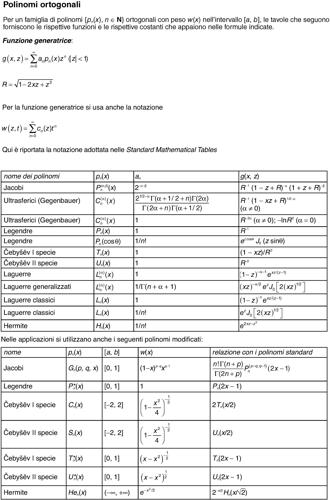
La formula per l’espressione analitica dei polinomi di Laguerre classici (con peso w(x) = e−x) è:
Per esempio:
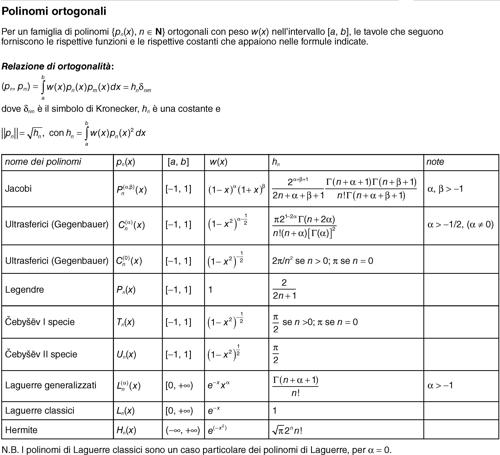
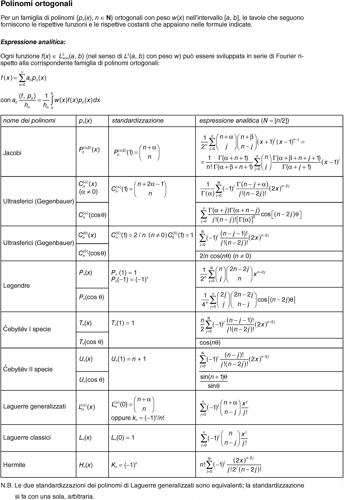
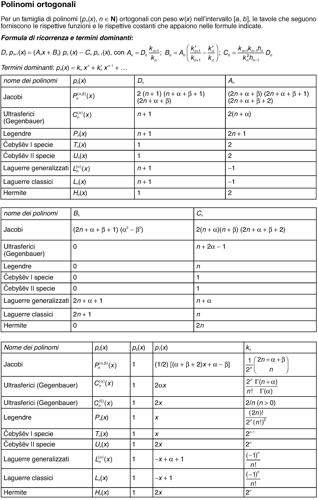
Nell’intervallo [−1, 1] e relativamente alla funzione peso w(x) = 1, essi possono essere definiti dalla formula ricorsiva:
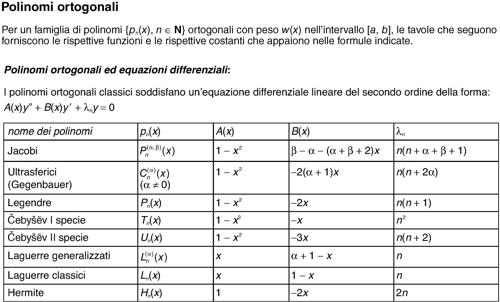
con n ≥ 2. Tali polinomi, che sono soluzione dell’equazione differenziale xy″ + (1 − x)y′ + ny = 0 (detta equazione di Laguerre), sono esprimibili anche nella forma
I polinomi di Laguerre intervengono nella descrizione della struttura radiale dell’atomo di idrogeno.