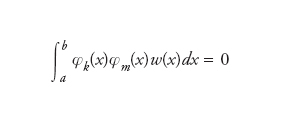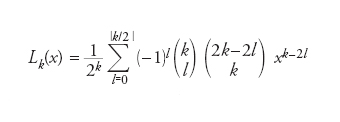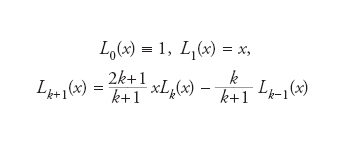polinomi ortogonali
polinomi ortogonali
Si consideri lo spazio vettoriale ℙn dei polinomi algebrici di grado minore o uguale a n e sia w:(a,b)→ℝ una funzione peso, ovvero una funzione non negativa e assolutamente continua nell’intervallo aperto (a,b). Il sistema di polinomi {φk(x)}nk=0, con φk∈ℙn, è detto ortogonale rispetto al peso w se
per k≠m. Qualora si considerino a=−1,b=1 e w(x)≡1 si ottiene la famiglia dei polinomi ortogonali di Legendre così definita:
per k≥0. Essa soddisfa la seguente relazione ricorsiva a tre termini:
per k≥1. Se invece, sempre sull’intervallo [−1, 1] si considera la funzione peso w(x)= =(1−x2)−1/2, si ottiene la famiglia dei polinomi di Chebyshev Tk(x)=cos(kθ), con θ=arccos x, per k≥0 che soddisfa la relazione ricorsiva a tre termini T0(x)≡1, T1(x)=x, Tk+1(x)=2xTk(x)−Tk−1(x) per k≥1. I polinomi precedentemente introdotti appartengono a una famiglia più ampia costituita dai polinomi di Jacobi {Jkα,β(x)}nk=0, ortogonali rispetto al peso w(x)=(1−x)α(1−x)β, per α,β>−1. Le basi di polinomi ortogonali vengono ampiamente utilizzate nell’ambito dell’approssimazione di funzioni e nella generazione di formule di quadratura di tipo interpolatorio altamente accurate.