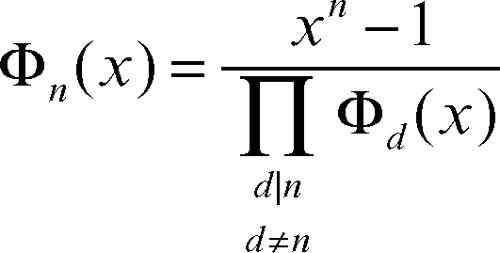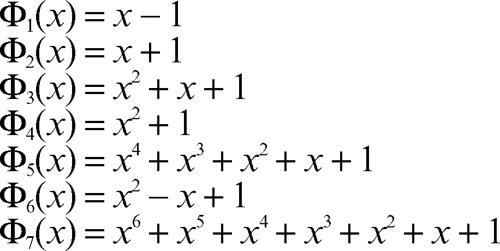polinomio ciclotomico
polinomio ciclotomico
polinomio ciclotomico polinomio monico a coefficienti interi che, per un opportuno numero naturale n, divide il polinomio xn − 1. In modo equivalente, esso può essere definito come il polinomio minimo sul campo Q dei numeri razionali di una delle radici (complesse) dell’unità. Da ciò deriva anche il suo nome giacché, nel piano di → Argand-Gauss, le radici ennesime dell’unità sono rappresentate come punti che dividono in n parti uguali la circonferenza di raggio unitario e rimandano quindi al problema della → ciclotomia. Più in particolare, se n è un numero naturale, si definisce l’ennesimo polinomio ciclotomico come il polinomio minimo su Q di una qualsiasi delle radici primitive n-esime dell’unità: esso è un polinomio monico a coefficienti interi di grado φ(n), dove φ indica la funzione di → Eulero. Se ζ1, ζ2, …, ζφ(n) sono le φ(n) radici primitive n-esime dell’unità, allora l’n-esimo polinomio ciclotomico Φn(x) si fattorizza sul campo C dei numeri complessi come segue:
Poiché i polinomi ciclotomici sono tutti irriducibili su Q e poiché le radici del polinomio xn − 1 sono tutte e sole le radici n-esime dell’unità, si ottiene la seguente fattorizzazione in polinomi irriducibili su Q:
dove la scrittura d |n indica che il prodotto è limitato a quegli indici d che dividono n. Tale fattorizzazione fornisce inoltre un algoritmo ricorsivo per il calcolo dei polinomi ciclotomici:
Segue da questa formula che, se p è un qualsiasi numero primo, allora vale
Sono indicati di seguito i primi sette polinomi ciclotomici (n = 1, 2, …, 7):