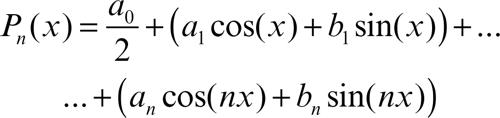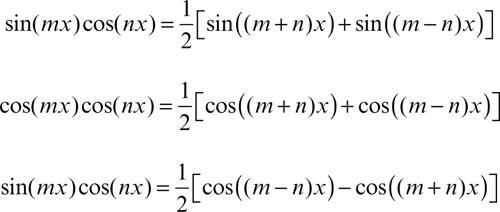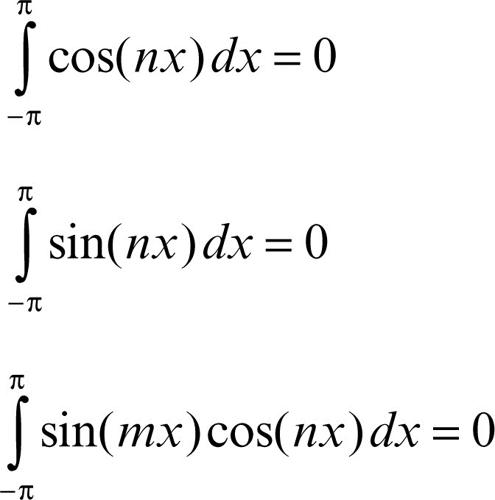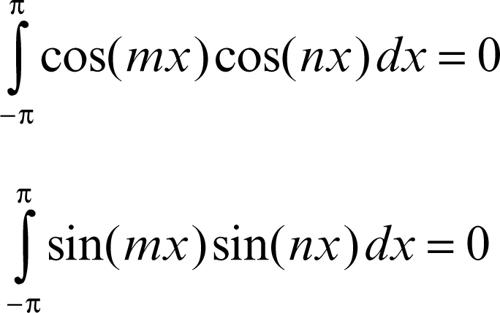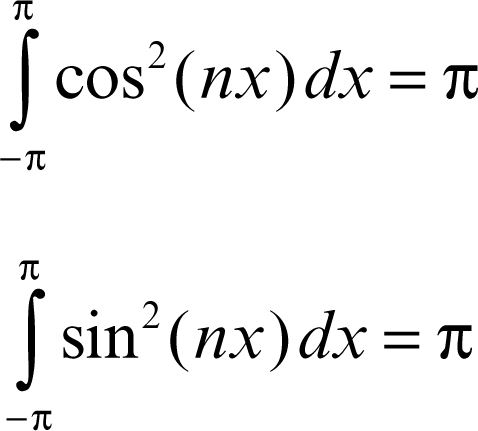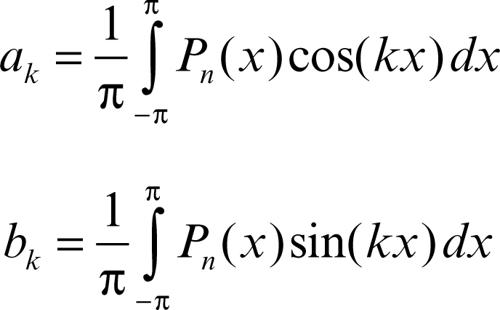Fourier, polinomio di

Fourier, polinomio di

Fourier, polinomio di in analisi, espressione di un qualunque polinomio a coefficienti in R, attraverso una combinazione lineare delle funzioni goniometriche di base, seno e coseno.

Un qualunque polinomio P_n(x), secondo Fourier, può infatti essere espresso nella forma

riscrivibile come

Le costanti a₀/2, a_i e b_i, con i = 1, ..., n sono dette coefficienti del polinomio P_n(x). Un polinomio di Fourier è quindi una ridotta della serie di Fourier.

I polinomi di Fourier sono funzioni periodiche di periodo 2π. Utilizzando le identità goniometriche

si dimostrano le formule integrali:

• per n ≥ 0:

• per n ≠ m:

• per n ≥ 1:

Con tali formule si dimostra che per il polinomio di Fourier P_n(x) si ha:

essendo 0 ≤ k ≤ n. Con lo sviluppo in polinomi di Fourier si stabilisce quindi una sintesi tra fenomeni esprimibili in forma algebrica e polinomiale (di per sé non periodici) e fenomeni che risultano come somma e prodotto di altri fenomeni trascendenti e intrinsecamente periodici. Tale equivalenza risulta particolarmente utile, nelle applicazioni, data la diversa trattabilità delle funzioni polinomiali rispetto a quelle trascendenti.