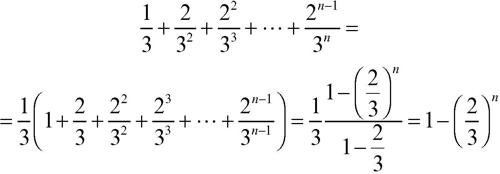Cantor, polvere di
Cantor, polvere di
Cantor, polvere di particolare sottoinsieme dei numeri reali, detto anche insieme ternario di Cantor, costruito con il seguente procedimento: si considera un segmento di lunghezza unitaria, per esempio l’intervallo chiuso [0, 1], lo si divide in tre parti uguali e si rimuove la parte centrale, ossia l’insieme aperto
Gli intervalli che rimangono sono [0, 1/3] e [2/3, 1]. Si itera il procedimento sugli intervalli rimasti, cancellando di volta in volta la parte centrale dei segmenti ottenuti, dopo che siano stati divisi in tre parti uguali. Dopo infinite iterazioni di questo tipo si ottiene un insieme di misura nulla; infatti, dopo n passi si cancella un insieme di sottointervalli la cui misura totale è:
Ciò significa che per n → ∞ la misura di tutti i segmenti cancellati tende a 1 e la polvere di Cantor, che rappresenta la parte rimanente dopo l’operazione di cancellatura, ha misura nulla. Si può anche dimostrare che, nonostante questa particolare proprietà metrica, la polvere di Cantor ha la cardinalità del continuo. Inoltre, poiché il suo complementare è l’unione di un insieme di aperti ed è, quindi, aperto, la polvere di Cantor è un insieme chiuso. È un insieme compatto e ha dimensione non intera, D = log32. La sua dimensione è, quindi, compresa tra 0 e 1. La polvere di Cantor è qualcosa “di più” di un insieme di punti (di dimensione 0) e “di meno” di una linea (di dimensione 1). La sua dimensione non intera è propria degli oggetti della geometria dei frattali (→ frattale).