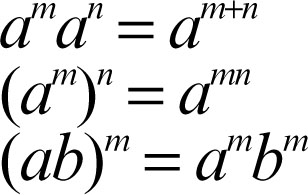potenza

potenza

potenza termine usato con significati diversi (→ insieme, potenza di un, o → cardinalità; → operatore, potenza simbolica di un; potenza di una → proiettività; → punto, potenza di un, rispetto a una circonferenza). In ambito numerico, è il risultato della operazione che associa a due numeri reali a e b il numero a^b (che si legge «a alla b» o «a elevato a b»): a è detto la base della potenza, b ne è detto l’esponente, e a^b indica il prodotto di b fattori tutti uguali ad a. La prima potenza di un numero è il numero stesso; la seconda potenza il suo quadrato, la terza il suo cubo. L’operazione di elevazione a potenza, definita in origine con esponente un numero naturale, è successivamente generalizzata ai numeri negativi e ad arbitrari esponenti razionali, reali e complessi, assumendo eventualmente che anche la base sia un numero complesso (si veda anche l’elevazione a potenza di un → polinomio).

Potenza con esponente naturale

Se l’esponente b = n è un numero naturale non nullo, allora tale numero indica il numero dei fattori uguali alla base che vanno moltiplicati tra loro:

dove, se a ≠ 0, si pone a⁰ = 1. Non ha significato la scrittura 0⁰. Valgono le proprietà delle potenze

Potenza con esponente intero

Se l’esponente b = −n è un intero negativo, la scrittura a⁻ⁿ (con a ≠ 0) equivale alla scrittura 1/aⁿ. Una potenza con base reale ed esponente intero è negativa se e solo se la base è negativa e l’esponente è dispari.

Potenza con esponente razionale

Se l’esponente b = n /m è un numero razionale, la scrittura a^n/m (con a > 0) equivale alla scrittura

vale a dire che su a si deve eseguire l’operazione di elevazione a potenza n-esima e di tale risultato si deve estrarre la radice m-esima. Per esempio, 4^−3/2 = 1/8, perché 4⁻³ = 1/64 e √(64) = 8.

Potenza con esponente irrazionale

Se l’esponente è un numero irrazionale x, la potenza a^x (sempre con a > 0) è definita per continuità: se {b_n} è una successione di numeri razionali convergente a x, si definisce allora il numero a^x come il limite, per n tendente all’infinito, della successione

Potenza con esponente complesso

L’operazione di elevazione a potenza può infine essere generalizzata assumendo che l’esponente b sia un arbitrario numero complesso w: in tal caso la potenza a^w è definita come il numero complesso a^w = e^wlog(a), dove log(a) indica il logaritmo naturale di a e dove e^w è il valore della funzione esponenziale nel campo complesso e^z per z = w.

Potenza con base ed esponente complessi

Ponendosi nell’ambito dei numeri complessi, l’operazione di elevazione a potenza può essere generalizzata anche a un’arbitraria base reale negativa o complessa: tuttavia, se l’esponente b non è un numero intero, si perde l’univocità dell’operazione: se per esempio a è un numero reale negativo e l’esponente b = n /m è un numero razionale, con n dispari e m pari, allora la scrittura

ha significato solamente nell’ambito dei numeri complessi e definisce l’insieme delle m radici m-esime del numero reale negativo aⁿ. Più in generale, se z e w sono due arbitrari numeri complessi, allora si definisce z^w = e^wlog(z), dove e^u indica la funzione esponenziale complessa e dove log(u) indica la funzione logaritmo complesso. Poiché la funzione logaritmo complesso è polidroma, fissando l’esponente w l’operazione di elevazione a potenza così definita individua una funzione polidroma dell’insieme C dei numeri complessi in sé stesso: per ogni z, la sua potenza z^w è un insieme in generale infinito i cui elementi differiscono tra loro per fattori che sono potenze intere di e^2πiw. Tale insieme è costituito da un solo elemento se e solo se l’esponente w è un numero intero mentre è finito se e solo se w è un numero razionale.