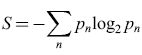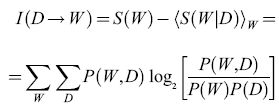Potenzialita e limitazioni nella misura della trasmissione dell'informazione neuronale
Potenzialità e limitazioni nella misura della trasmissione dell'informazione neuronale
Nel tentare di descrivere cosa accade nel cervello usiamo idee molto qualitative: diciamo che certe cellule o circuiti 'estraggono informazioni' su alcune caratteristiche del mondo sensoriale che ci circonda, o che l'attività in certi neuroni 'rappresenta' i segnali sensoriali o le azioni motorie. Nell'indagare le strutture di queste rappresentazioni siamo soliti dire che gli aspetti specifici delle risposte neuronali costituiscono un codice. È naturale chiedersi se si possa dare una precisa formulazione quantitativa a qualcuna di queste idee. In questo saggio descriverò gli argomenti secondo i quali la teoria dell'informazione di Shannon è l'unico sistema corretto di riferimento per rispondere a molti interrogativi sulle funzioni cerebrali. In seguito, descriverò una serie di esperimenti realizzati secondo la teoria dell'informazione e mostrerò come questi esperimenti abbiano prodotto nuovi e talvolta inaspettati paradigmi conoscitivi sul problema della codifica neuronale. I risultati di questi esperimenti hanno suscitato nuove domande sia dal punto di vista teorico che sperimentale.
Introduzione
La pubblicazione di questo saggio coinciderà, più o meno, con il cinquantenario dei lavori classici di C. Shannon sulla teoria dell' informazione. Fin dall' inizio, molti studiosi, compreso lo stesso Shannon, sperarono che la teoria dell'informazione potesse fornire non soltanto una guida per il progetto di sistemi di comunicazione artificiali, ma anche un contesto matematicamente preciso per l'analisi dei sistemi di trasmissione ed elaborazione dell'informazione che si presentano in natura, negli esseri umani e negli altri animali. Il sogno era, in breve, che la teoria dell'informazione potesse costituire l'inizio di una teoria del funzionamento del cervello.
Il sogno di un approccio allo studio del cervello basato sulla teoria dell'informazione è molto attraente, ma vi sono anche buoni motivi per essere scettici al riguardo. Messi da parte i grandi sogni, scopo di questo saggio è chiedersi se la teoria dell'informazione possa fornire una guida su come progettare e analizzare nuovi esperimenti: può la teoria di Shannon fornire un metodo efficace per lo studio del funzionamento del cervello? lo credo che la risposta a questa modesta domanda sia un netto "sì", sebbene il cammino che conduce a questa conclusione non sia stato semplice. C'è attualmente un rinnovato interesse per le applicazioni della teoria dell'informazione al sistema nervoso, ma sull'opinione qui sostenuta non c'è affatto un consenso unanime. In questo saggio cercherò di delineare i contributi specifici e concreti che gli approcci basati sulla teoria dell'informazione stanno dando allo studio della dinamica dell'elaborazione dell'informazione nel cervello. In particolare, sarà posta attenzione sui tentativi di misurare le quantità fondamentali che caratterizzano, in base alla teoria dell'informazione, il funzionamento dei singoli neuroni e dei loro raggruppamenti. Vorrei fosse chiaro che si possono effettuare misure a prescindere da qualunque filosofia specifica sulla teoria ultima del cervello. La speranza è in effetti che il risultato degli esperimenti più quantitativi fornisca una guida verso nuove prospettive teoriche. Molti degli argomenti trattati sono discussi in maggior dettaglio in un libro recente (Rieke et al., 1997), che contiene anche riferimenti bibliografici più completi.
Le basi teoriche
Si consideri il caso di due amiche, Fannie e Ruth, che stanno conversando. Fannie chiede a Ruth cosa pensi di una notizia apparsa in prima pagina nel giornale del mattino. Fannie conosce molto bene Ruth. Sa che parla molto correttamente ed è attenta a seguire le regole grammaticali anche in una conversazione informale. Sa anche che di solito usa modi di dire facili da identificare ed elencare e, avendo avuto con lei molte discussioni di politica, sa abbastanza bene come Ruth reagirà alle ultime notizie. Fannie può dunque fare un elenco delle possibili risposte di Ruth alla sua domanda e a ognuna di queste può assegnare una certa probabilità. Da questa lista di possibilità e probabilità si può calcolare una funzione entropia, analogamente a quanto si fa per determinare l' entropia di un gas in termodinamica o in meccanica statistica. Se la probabilità della nesima risposta è Pn, l'entropia è
formula. [
l]
L'entropia S misura l'incertezza di Fannie sulla risposta che Ruth darà alla sua domanda. Quando Ruth risponde, tale incertezza scompare, poiché è stata data in effetti una delle risposte, per la quale p = l, e nessuna delle altre, per le quali p = O, cosicché l'entropia è ridotta a zero. Dal punto di vista intuitivo, appare ovvio identificare la riduzione di incertezza con l'informazione acquisita nell'ascoltare la risposta di Ruth. Shannon ha dimostrato che questa identificazione non solo è intuitivamente ovvia, ma è anche la sola definizione di informazione compatibile con alcuni semplici vincoli.
lnnanzitutto, Shannon ipotizza che l'informazione acquisita nell' ascoltare la risposta si possa scrivere come funzione delle probabilità Pn. Inoltre, se tutte le N risposte avessero la stessa probabilità, pari a Pn = l/N, l'informazione acquisita dovrebbe essere una funzione monotona crescente di N. Un altro vincolo consiste nel fatto che, se la domanda fosse composta di due parti completamente indipendenti l'una dall'altra, l'informazione totale acquisita dovrebbe essere pari alla somma dell'informazione acquisita dalle risposte alle singole parti della domanda. lnfine, domande più generali, costituite da molte parti, si possono concepire come alberi ramificati, in cui la risposta a ogni parte della domanda fornisce un ulteriore miglioramento della stima delle probabilità; in questo caso dovremmo poter scrivere l'informazione totale acquisita come una media pesata dell'informazione acquisita in ogni punto di diramazione. Shannon dimostrò che l'unica funzione delle {Pn} coerente con questi tre postulati (monotonicità, indipendenza e ramificazione) è, a meno di una costante moltiplicativa, l'entropia S. In fisica, la costante moltiplicativa è spesso identificata con la costante di Boltzmann, kB, ma questo non è essenziale. Nel misurare l'informazione ha più senso mantenere S in forma adimensionale. Qualsiasi costante adimensionale può quindi essere assorbita nella base del logaritmo; scegliendo, in particolare, i logaritmi in base due si ottiene la misura dell'informazione in unità binarie, detta bit.
La maggior parte dei testi elementari di termodinamica e di meccanica statistica introducono l'entropia come misura di incertezza, o mancanza di informazione sullo stato microscopico del sistema, lasciando tuttavia solo una vaga idea nella mente dello studente. Il teorema di Shannon, la cui dimostrazione occupa meno di due pagine nell'articolo originale di Shannon e W. Weaver (1949), trasforma questa idea vaga in un risultato matematico preciso.
Si è ipotizzato che, nella conversazione tra Fannie e Ruth, Fannie riceva una risposta completa alla sua domanda, e quindi la sua incertezza venga eliminata. Questa è naturalmente un'idealizzazione. Un'ipotesi più naturale consiste nel supporre che il mondo possa trovarsi in diversi stati W e, osservando i dati D, si apprenda qualcosa, ma non tutto, su questi stati. Si suppone che, in assenza di osservazioni, gli stati del mondo siano caratterizzati da una certa distribuzione di probabilità P(W), a cui corrisponde un'entropia S(W). Dopo aver osservato i dati particolari D, la conoscenza di W è descritta dalla distribuzione di probabilità condizionata P(WID), a cui corrisponde l'entropia S(WID). Identificando ora la riduzione di entropia con l'informazione acquisita su W, e mediando su tutti i possibili dati, pesati con la loro probabilità P(D), si ottiene l'informazione media fornita da D su W, pari
formula. [2]
Nell'equazione [2], l'informazione fornita da D su W è una funzione simmetrica rispetto a D e W. Questo significa che lo stato del mondo fornisce una quantità di informazione sui dati oservativi che risulta, in media, uguale all'informazione fornita dai dati medesimi sullo stato del mondo. Perciò l'informazione fornita è spesso chiamata informazione mutua, e questa proprietà di simmetria risulterà importante nella discussione sul codice neuronale.
Alcuni concetti fondamentali
La teoria dell'informazione fornisce gli strumenti idonei a quantificare le risposte dei neuroni, e anche alcuni concetti fondamentali che permettono, in diversi casi, di formulare in modo più preciso le domande sul funzionamento del cervello.
Limiti fisici alla trasmissione dell'informazione
Se si osserva un segnale, per esempio la sequenza di potenziali d'azione prodotti da un neurone nel cervello, la quantità di informazione acquisibile, in qualunque contesto, ha come limite superiore l'entropia del segnale osservato. In alcuni casi, vale un'affermazione ancora più limitativa: si supponga di enumerare alcuni eventi discreti (per esempio, potenziali d'azione, vescicole sinaptiche o automobili) e di contare in media n ̄ eventi. Ciò fissa un valore massimo all'entropia che dipende solo da n ̄, e quindi il solo fatto di contare gli eventi fissa un limite superiore all'informazione acquisibile (Rieke et al., 1997). La formula esatta che esprime questo limite è meno importante del concetto: se un sistema codifica segnali mediante 'quanti' discreti e identici, l'informazione che si può trasmettere ha un limite rigoroso che dipende dal numero medio di 'quanti' che il sistema sta utilizzando.
Fenomeni di quantizzazione sono comunemente presenti, a vari livelli, nello scambio di segnali fra neuroni. La visione ha inizio con il conteggio di fotoni, e il meccanismo di amplificazione nei fotorecettori funziona mediante un numero limitato di molecole. Analogamente, nell'orecchio interno ogni recettore converte i segnali da meccanici a elettrici in canali discreti, formati da un centinaio di molecole. In ogni sinapsi chimica, anche quando la risposta elettrica di una cellula è di tipo continuo (come avviene nella retina), il segnale sinaptico viene 'quantizzato' nelle vescicole. Infine, la maggior parte delle cellule del sistema nervoso centrale produce potenziali d'azione discreti, ovvero degli impulsi. In ogni situazione, quindi, ci sono limiti fisici alla trasmissione dell'informazione, derivanti direttamente dalla 'quantizzazione'. Una cosa che abbiamo imparato dalle misure di trasmissione dell'informazione è che, almeno in qualche caso, i cervelli reali funzionano in regimi prossimi a questi limiti fisici, come avrò modo di far notare negli esempi che seguono.
La struttura d'insieme degli stimoli
Nel mondo reale il cervello ha a che fare con segnali molto complessi. In particolare, non è noto a priori se i segnali che percepiremo nel prossimo istante facciano parte di un insieme limitato, né su quale scala temporale gli stimoli possano variare in modo significativo. Invece di pensare che il mondo presenti ai nostri occhi e alle nostre orecchie uno stimolo dopo l'altro, può essere più utile pensare agli stimoli come a funzioni casuali del tempo, che seguono una distribuzione di probabilità piuttosto complessa. Questa distribuzione, in natura o negli esperimenti di laboratorio, definisce la struttura d'insieme degli stimoli. Supponiamo di registrare le immagini che giungono alla retina, o le forme d'onda acustiche sul timpano, o i segnali motori inviati alle mani; questa distribuzione di probabilità dei segnali naturali può essere campionata, e in effetti sono stati eseguiti alcuni esperimenti di questo tipo. Molti di questi segnali naturali hanno caratteristiche comuni: una dinamica su diverse scale temporali (e, per la visione, spaziali) che spesso si avvicinano all'invarianza di scala o all'autosomiglianza (selfsimilarity), e un intervallo dinamico enorme, cosicché la distribuzione di probabilità delle ampiezze del segnale ha code molto lunghe di segnali 'forti', e un picco pronunciato intorno al 'silenzio' completo.
A differenza dei segnali complessi che si presentano in natura, la maggior parte degli esperimenti sulle risposte dei neuroni sensoriali viene effettuata utilizzando stimoli drasticamente semplificati. In tal modo gli stimoli semplificati possono essere parametrizzati, e si può quindi analizzare la risposta del sistema al variare dei parametri significativi. Ciò che è noto sull'elaborazione dell'informazione sensoriale è stato in gran parte dedotto in questo modo. Tuttavia, gli esperimenti di questo tipo non risolvono il problema di come il sistema elabori i segnali presenti in natura. È possibile caratterizzare le relazioni di input-output dei neuroni per stimoli semplici, e predire da queste le risposte a stimoli più complessi? Il cervello è in qualche modo 'sintonizzato' con la struttura dei segnali che si presentano nel mondo reale? Queste sono domande di fondo, ma difficili da affrontare, in parte a causa del fatto che non è chiaro come si dovrebbe caratterizzare la risposta neuronale agli stimoli complessi. La teoria dell'informazione fornisce un possibile metodo di indagine, che consiste nel definire l'informazione che i neuroni forniscono sulla base degli ingressi sensoriali, senza alcuna ipotesi circa la semplicità dell'insieme degli stimoli, e nel confrontare le rappresentazioni di stimoli provenienti da insiemi diversi. Almeno in qualche caso, sembra in effetti che i primi stadi dell'elaborazione sensoriale forniscano una codifica più efficiente e più ricca di informazione per i segnali naturali.
La struttura dei codici neuronali
I segnali che descrivono il mondo sensibile sono continui: la riflettanza delle superfici, le traiettorie del moto, la dipendenza temporale della pressione sonora o della concentrazione olfattiva. Analogamente, il segnale di uscita motorio di un organismo consiste in forze e movimenti che non sono discreti o 'quantizzati'. Ciononostante, la maggior parte dei neuroni del cervello non produce segnali elettrici continui, ma genera piuttosto sequenze di impulsi discreti e identici, chiamati potenziali d'azione. È evidente che queste sequenze di impulsi costituiscono una codifica dei segnali sensoriali o motori. Settanta anni fa, E.D. Adrian osservò che i neuroni sensoriali, in risposta a stimoli costanti, producono impulsi a frequenza crescente con l'intensità o l'ampiezza dello stimolo, e questa codifica basata sulla frequenza ha guidato l'esplorazione di aree cerebrali precedentemente sconosciute.
L'interpretazione degli esperimenti di Adrian ha tuttavia lasciato inevase diverse domande, raggruppate di solito sotto il titolo di temporizzazione degli impulsi: in presenza di stimoli costanti, può la sequenza temporale dei potenziali d'azione trasferire informazione, oltre quella trasmessa dalla frequenza degli impulsi? In un insieme di cellule, può la produzione di impulsi simultanei in molteplici cellule avere un significato speciale? In presenza di stimoli di tipo naturale, e dinamici, è possibile che la temporizzazione di singoli impulsi evidenzi eventi particolari dell'ingresso sensoriale e, almeno in caso affermativo, con quale precisione questa temporizzazione può agire? Ognuna di queste domande può essere formulata in forma corretta, utilizzando concetti tratti dalla teoria dell'informazione, e almeno in qualche caso, questo metodo ha portato a risposte chiare e decisive dalle quali è emerso cosa significa la comprensione del codice neuronale.
Il concetto di informazione 'su qualcosa'
L'entropia misura la variabilità di un segnale. Se un segnale possiede una propria struttura spaziale o temporale, questo ne limita la variabilità, e di conseguenza ne diminuisce l'entropia. L'identificazione dell'entropia con l'informazione fa supporre che i segnali strutturati siano meno ricchi di informazione, il che è contrario al senso intuitivo comune. È infatti naturale pensare che si riceva meno informazione osservando segnali casuali o privi di struttura, mentre si ha l'impressione che i segnali dotati di struttura più elaborata (per esempio, il linguaggio) siano quelli più ricchi di contenuto informativo. La difficoltà risiede nel fatto che l'entropia e l'informazione, pur essendo fra loro legate, non sono identiche. L'entropia misura l'informazione disponibile, e cioè la capacità di un segnale di trasportare informazione. Una domanda diversa è se il segnale fornisca in effetti informazione fino a raggiungere la sua capacità, e non si può rispondere senza considerare qualcosa che vada al di là del segnale stesso.
Si consideri, infatti, un insieme di forme d'onda acustiche, ottenute registrando in forma digitale brevi tratti di conversazione tra persone. L'entropia di queste forme d'onda può essere facilmente calcolata a partire dalla distribuzione delle forme d'onda nell'insieme considerato. In termini pratici, può essere difficile disporre di un numero sufficiente di dati per campionare in modo affidabile queste distribuzioni; tuttavia, concettualmente è sufficiente supporre di possedere un campione di registrazioni di grandi dimensioni. Ci possiamo chiedere quale sia il contenuto di informazione di queste forme d'onda. Ma per rispondere a questa domanda ci si deve porre un'altra questione: informazione su che cosa? Se, per esempio, interessa sapere quanta informazione è contenuta nelle registrazioni con riferimento alle effettive forme d'onda acustiche, occorre integrare i dati con una caratterizzazione del rumore e della distorsione nel processo di registrazione. Se, più probabilmente, interessa l'informazione che le registrazioni forniscono su una trascrizione fonetica, o testuale, di una conversazione, occorre disporre effettivamente della trascrizione, per poterne valutare il contenuto informativo. A un livello più astratto, si potrebbe essere interessati in realtà alle intenzioni o allo stato cognitivo interno di chi parla, e non a ciò che ha detto, ma a ciò che intendeva dire, o a quello di cui stava parlando, e in questi casi sarebbe certamente difficile disporre dell'equivalente di una trascrizione. Il punto è che, a differenza dell'entropia, l'informazione è sempre 'informazione su qualcosa', e in assenza di una definizione precisa del 'qualcosa' non è nemmeno possibile iniziare a usare i concetti della teoria dell'informazione per analizzare segnali o sistemi. Nello studio delle risposte neuronali, interessa spesso sapere quali caratteristiche del mondo sensoriale vengano rappresentate da particolari neuroni. La teoria dell'informazione consente di quantificare non solo l'informazione che un neurone trasmette sull'intero segnale, ma anche quella che il neurone trasmette rispetto a singole parti o caratteristiche del segnale. Dovrebbe essere quindi possibile rappresentare in modo quantitativo la nozione qualitativa di selettività rispetto a certe caratteristiche, e verificare che l'informazione su certe particolari caratteristiche costituisce in realtà tutta l'informazione che il neurone trasmette sull'intero stimolo sensoriale. Per quanto ne so, questo non è ancora stato fatto.
Risultati sperimentali
Nonostante gli scienziati siano soliti considerare i neuroni 'portatori d'informazione' riguardanti i segnali provenienti dal mondo esterno, solo recentemente sono stati effettuati esperimenti in cui questa informazione viene misurata. L'ordine di esposizione dei prossimi paragrafi va dai problemi più semplici a quelli più complessi, sebbene non sono proprio certo che gli esperimenti possano essere inquadrati in una linea concettuale univoca.
La prima sinapsi nel sistema visivo della mosca
Sebbene la rappresentazione del mondo sensoriale all'interno dei nostri cervelli si basi su potenziali d'azione discreti, o impulsi, in molti sistemi visivi, incluso il nostro, la rivelazione e l'elaborazione della luce nei primi stadi vengono effettuate da neuroni che non producono impulsi. Questo vale anche per il sistema visivo della mosca, nel quale R. de Ruyter van Steveninck e S.B. Laughlin (1996) hanno misurato i valori più alti del tasso di trasmissione dell'informazione finora osservati in qualsiasi neurone. Questo lavoro presenta diversi aspetti interessanti, che illustrano cosa si possa imparare da un'analisi quantitativa della caratterizzazione dei neuroni, sulla base della teoria dell'informazione.
Per trasmettere l'informazione relativa al segnale, il sistema, per esempio la cellula fotorecettrice della mosca, deve fornire una risposta variabile nel tempo ma legata, in modo più o meno deterministico, alle variazioni del segnale. Si supponga di sottoporre al fotorecettore un segnale luminoso la cui intensità vari intorno a un certo livello di sfondo. Se la stessa sequenza di immagini (a un solo pixel) è presentata più volte, ogni volta l'andamento della risposta sarà leggermente diverso. Mediando tutte queste risposte si estrae una componente deterministica, mentre dalla differenza di tali risposte rispetto al valore medio si ottiene un segnale variabile, assimilabile a una componente di rumore. Sulla base di variazioni d'intensità comprese in un ragionevole intervallo, de Ruyter van Steveninck e Laughlin hanno dimostrato che la tensione media di risposta del fotorecettore è funzione lineare dell'intensità o del contrasto della sequenza di immagini, e che la componente di rumore segue una legge di distribuzione gaussiana delle fluttuazioni di tensione intorno alla media. Questa è certamente una situazione facile da analizzare.
La prima osservazione da fare consiste nel considerare il rumore presente nella risposta non come una fluttuazione di tensione, ma come un rumore aggiunto alle immagini osservate. Poiché le fluttuazioni hanno una distribuzione gaussiana, possono essere completamente caratterizzate dal loro spettro di potenza, che misura la varianza delle fluttuazioni che hanno luogo alle diverse frequenze. Questo rumore efficace ha un livello minimo che è fissato dalle leggi della fisica: il segnale luminoso è composto da fotoni discreti che arrivano in modo casuale, e la struttura statistica di questi arrivi ci consente di calcolare il livello di rumore efficace. Il rumore associato ai fotoni è 'bianco', poiché tutte le frequenze vi sono ugualmente rappresentate. In un ampio intervallo di intensità luminose e di frequenze di sfondo, i fotorecettori della mosca hanno livelli di rumore efficace che raggiungono il limite fissato dalla statistica dei fotoni. Ad alte frequenze c'è un eccesso di rumore che supera il limite fisico, e questo rumore fissa la risoluzione temporale del sistema.
Lo spettro di potenza del rumore efficace indica, in definitiva, quali segnali i fotorecettori possano e non possano trasmettere. È possibile esprimere queste misure in unità binarie (bit)? Un metodo consiste nell'assumere che la mosca viva in un ambiente particolare, e nel calcolare in seguito la quantità di informazione che il fotorecettore può fornire su questo particolare ambiente. Ma per caratterizzare il fotorecettore stesso, è opportuno porsi una diversa domanda: quanta informazione può trasmettere, in linea di principio, la cellula? Per rispondere, si supponga di disporre di un ambiente la cui struttura statistica utilizzi in modo ottimale il fotorecettore (probabilmente nel corso dell'evoluzione è accaduto l'inverso!). Questo problema di ottimizzazione può sembrare complesso, tuttavia, per un sistema con risposta lineare e rumore gaussiano esso è relativamente facile, ed è stato risolto da Shannon. Sulla base di tale soluzione, de Ruyter van Steveninck e Laughlin furono in grado di dedurre dalle misure dei segnali e del rumore le stime della capacità di trasmettere informazione di queste cellule. Questo fu fatto sia per i fotorecettori che per le grandi cellule monopolari, che ricevono uno stimolo sinaptico diretto da un gruppo di sei recettori.
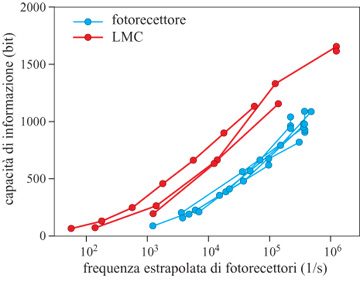
I risultati sulla capacità di trasmettere informazione nella retina della mosca sono riassunti nella figura (fig. 1). La prima cosa da notare è la scala: singoli neuroni sono in grado di trasmettere ben più di 1000 bit al secondo. Ciò non vuoI dire che questa capacità venga effettivamente utilizzata in condizioni naturali, ma piuttosto mostra quale sia la precisione dei meccanismi preposti alla rivelazione e alla trasmissione dei segnali nel sistema. In secondo luogo, si osserva che la capacità di trasmissione dell'informazione è funzione crescente del livello luminoso dello sfondo. Così, il rumore dovuto alla statistica dei fotoni diventa meno importante in condizioni di forte illuminazione, e questa riduzione del limite fisico migliora in effetti le prestazioni del sistema anche fino a frequenze di conteggio dei fotoni molto alte. Ciò indica, ancora una volta, che il limite fisico è rilevante ai fini delle prestazioni reali. Infine, nelle grandi cellule monopolari, l'informazione è stata trasmessa tramite una sinapsi e, nel corso di questo processo, viene convertita da un segnale di tensione continuo in una serie di eventi discreti corrispondenti al rilascio, da parte delle vescicole, di neurotrasmettitori nel sito sinaptico. Ne risulta un nuovo limite alla trasmissione dell'informazione, che deriva dal considerare le cellule monopolari come dei 'contatori di vescicole'. Se ogni vescicola dà un contributo misurabile e deterministico alla risposta della cellula (che è un assunto ottimistico), la risposta della grande cellula monopolare è equivalente a riferire quante vescicole sono state contate in una piccola finestra temporale corrispondente alla risoluzione temporale del fotorecettore. Pur non essendo nota la distribuzione di questi conteggi, è possibile stimare (da altri esperimenti, con qualche incertezza) il conteggio medio, ed è noto che, fissata la media, c'è un'entropia massima per ogni distribuzione di conteggi. Nessun meccanismo sinaptico può trasmettere più informazione di quella stabilita da questo limite. È importante il fatto che nella mosca ci si mantiene al di sotto di questo limite entro un fattore due, e l'accordo potrebbe essere ancora migliore, se non fosse per le incertezze sulla frequenza di conteggio delle vescicole (Rieke et al., 1997). Una discussione di problemi analoghi nel conteggio di fotoni da parte dell'occhio dei vertebrati è stata fatta da F. Rieke e DA Baylor (1998).
Riassumendo, la misurazione del tasso di trasmissione dell' informazione nella retina della mosca permette di trarre diverse importanti conclusioni. In primo luogo, il sistema è limitato dall'arrivo casuale dei fotoni, in un intervallo dinamico sorprendentemente ampio. Il rumore biologico è stato soppresso, e questo pone vincoli severi ai meccanismi molecolari della trasmissione dei segnali in queste cellule. In secondo luogo, la capacità di informazione delle cellule e delle sinapsi nei primi stadi della visione è molto alta. Si pensa a volte che il sistema visivo sia costretto a scartare informazioni poiché è incapace di gestire l'enorme flusso di dati che giunge attraverso l'occhio; in realtà, almeno all'inizio, il sistema ha una capacità enorme, e un'informazione scartata può essere considerata il risultato di una selezione attiva di ciò che è interessante per il cervello, e non una mossa estrema per limitare il flusso dei dati. Infine, sebbene le sinapsi siano in molti casi caratterizzate come elementi probabilistici e inaffidabili, in questo sistema la trasmissione dell'informazione attraverso la sinapsi avviene a un ritmo vicino al limite fissato dalla 'quantizzazione' del segnale in vescicole. Anche se dal punto di vista anatomico questa sinapsi è particolare, questi risultati pongono vincoli ai modelli degli eventi molecolari che controllano il rilascio delle vescicole, e c'è un ampio consenso sul fatto che questi meccanismi molecolari siano universali.
La decodifica dei segnali meccanici nel grillo e nella rana
I grilli, gli scarafaggi e le specie affini hanno particolari sensori meccanici, che si estendono dai loro lati posteriori, chiamati cerci. Ognuno dei due cerci è coperto di peli, e ogni pelo proviene da una singola cellula nervosa afferente. I peli si muovono in risposta a perturbazioni dell'aria, e la sequenza dei potenziali d'azione nella cellula nervosa codifica il movimento dell' aria. L'insieme di questi segnali (fino a diverse migliaia) viene utilizzato dall'animale per prendere decisioni sull'identità e sulla posizione degli oggetti in movimento nell'ambiente circostante. Tra le altre cose, questo è il sistema sensoriale che avvisa lo scarafaggio dell'avvicinarsi del piede dell'uomo. Nel grillo c'è un insieme di neuroni di secondo ordine che sembrano costruire una mappa delle direzioni del vento. Tale mappa fornisce un semplice test per la verifica delle ipotesi sulla codifica da parte di una popolazione di cellule. Come primo passo, è interessante interpretare la rappresentazione del movimento dei peli in termini di sequenze di impulsi delle cellule sensoriali afferenti. La teoria dell'informazione è stata utilizzata da alcuni studenti, guidati da J.P. Miller e G.W. Jacobs, per caratterizzare la codifica nel sistema dei cerci del grillo. In questa sede saranno descritti alcuni dei primi esperimenti compiuti da D. Warland e M. Landolfa (Warland et al., 1992).
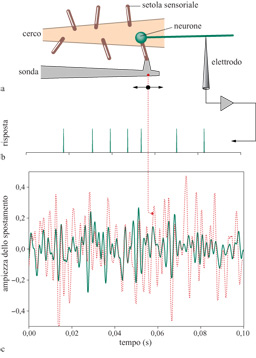
Un semplice esperimento consiste nell'afferrare un singolo pelo sensoriale, muoverlo in modo controllato e variabile nel tempo, e registrare la sequenza dei potenziali d'azione generati nella corrispondente cellula nervosa sensoriale. Questa è una versione abbastanza pura del problema della codifica neuronale, poiché nessuna sinapsi si interpone tra il segnale sensoriale e la sequenza di impulsi che ne deriva, né c'è, come nell'orecchio interno, una complessa preelaborazione meccanica del segnale. Tuttavia, anche in questo semplice caso, è difficile fornire una caratterizzazione diretta della corrispondenza tra segnali e sequenze di impulsi, poiché sia lo spazio degli stimoli che quello delle risposte hanno una dimensionalità molto elevata. Sono quindi opportune alcune semplificazioni. Un'idea consiste nel provare a decodificare la risposta neuronale, effettuando una traduzione inversa nello spazio dei segnali sensoriali. Su queste basi, è possibile confrontare i segnali veri con le stime migliori derivate dalle sequenze di impulsi, e la qualità della corrispondenza tra la realtà e la stima neuronale si può quantificare in bit. Naturalmente, la procedura di decodifica non può estrarre l'informazione che non era contenuta nella risposta neuronale; al contrario, è possibile perdere informazione a causa di una cattiva decodifica. La strategia di decodifica (realizzata con cura) fornisce quindi un limite inferiore all'informazione contenuta nella risposta neuronale. Confrontando questo limite con qualche misura più assoluta, del tipo di quelle discusse in seguito, è possibile effettuare una significativa verifica della comprensione del codice, così come è stato implementato negli algoritmi di decodifica.
La decodifica può essere effettuata nel seguente modo. Se gli impulsi sono eventi rari, allora ogni impulso fornisce l'informazione sullo stimolo che si trova in una piccola finestra temporale intorno a esso, e queste finestre si sovrappongono solo di poco. In queste condizioni, indipendentemente dalla complessità del processo di codifica, la decodifica deve essere possibile semplicemente addizionando i contributi provenienti dai singoli impulsi, e a questo si è dato il nome di decodifica lineare, o ricostruzione lineare dei segnali sensoriali. Questa idea ha le sue origini nel lavoro teorico di A. Zee e di chi scrive, e negli esperimenti sul sistema visivo della mosca, discussi nel seguito (de Ruyter van Steveninck e Bialek, 1988; Bialek e Zee, 1990; Bialek et al., 1991). Il punto veramente importante, cioè il fatto che la decodifica lineare può avvenire in neuroni che codificano i segnali tramite regole altamente non lineari, non veniva sottolineato nell'articolo originale (v. anche Rieke et al., 1997).
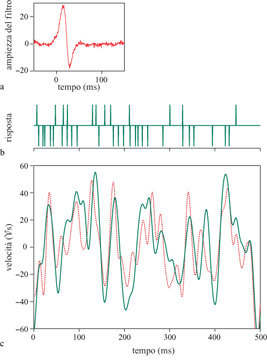
La figura (fig. 2) mostra i risultati delle ricostruzioni lineari nel sistema dei cerci del grillo, per il semplice esperimento sopra descritto. Si vede a occhio che le ricostruzioni hanno alcune caratteristiche favorevoli, altre meno. Risulta che queste ricostruzioni sono una versione accurata e regolarizzata dei segnali reali con un po' di rumore aggiunto, e il rumore è quasi gaussiano. Il rumore è piccolo, e ciò vuoI dire che le sequenze di impulsi provenienti da un singolo neurone consentono di stimare la traiettoria del pelo con la precisione di un centesimo di grado, se l'integrazione è condotta per un secondo. Da questo livello di rumore, e dalla distribuzione dei segnali usati nell'esperimento, si può ricavare che il neurone sta trasmettendo almeno 294 bit al secondo di informazione sullo stimolo. Quando fu effettuato l'esperimento un valore così alto fu ritenuto sorprendente, poiché corrispondeva a 3 bit di informazione per ogni impulso. Tale valore può essere tuttavia giustificato. Infatti, se ogni spostamento di un microsecondo nella temporizzazione di un impulso potesse segnalare qualcosa di significativo sullo stimolo, il neurone sarebbe in grado di trasmettere una quantità di informazione davvero enorme. Qual è la risoluzione temporale di questo sistema? Data una risposta neuronale, se ogni impulso viene spostato, in modo indipendente e casuale, con una deviazione standard di 0,3 ms, la qualità della ricostruzione non è quasi alterata, e il tasso di informazione cambia solo di pochi punti percentuali. A questa risoluzione temporale, però, l'entropia della sequenza di impulsi è di soli 6 bit per impulso. Il grillo sta quindi operando entro un fattore due al di sotto del limite fisico imposto alla trasmissione dell' informazione. Per noi, e per la maggior parte degli altri animali vertebrati, i sensori meccanici più sensibili si trovano nell'orecchio interno. Le rane, tra gli altri animali, hanno un organo nell'orecchio interno che avverte le vibrazioni, detto sacculo. In alcune specie di rana, questo organo è sensibile a vibrazioni davvero piccole; per esempio, se la terra vibra di circa 0,01 nm, i neuroni cambiano la loro sequenza di emissione abbastanza da consentire una rivelazione affidabile di questi movimenti su scala atomica (Narins e Lewis, 1984). La maggior parte delle rane usa questo sistema sensoriale per rivelare il rumore dei passi dei predatori in avvicinamento, ma alcune specie comunicano con altre rane battendo colpi sul terreno. Il sacculo della rana fornisce un altro sensore meccanico accessibile, per mezzo del quale è possibile indagare sul contenuto informativo di una sequenza di impulsi e sull'efficienza della codifica. Confrontando gli esperimenti sui due sistemi, quasi tutti i parametri naturali appaiono diversi: la distanza evolutiva tra i grilli e le rane è enorme, il sacculo della rana è sensibile a frequenze più basse, le frequenze medie degli impulsi sono minori, e l'analisi della ricostruzione dello stimolo mostra che il tasso complessivo di trasmissione dell'informazione è anch'esso minore. È dunque sorprendente il fatto che l'informazione per impulso sia quasi la stessa, circa 3 bit per impulso, e sebbene la risoluzione temporale naturale sia minore (circa 2,5 ms invece di circa 0,25 ms), adottando questa risoluzione, l'efficienza di codifica è nuovamente circa il 50%. In effetti, un simile livello di efficienza di codifica è stato stabilito per una varietà di neuroni visivi, dai neuroni sensibili al movimento del sistema visivo della mosca (si veda più avanti) alle cellule gangliari della retina delle salamandre e dei conigli, fino alle cellule del nucleo genicolato laterale dei gatti. Non è un fatto ovvio che i limiti teorici alla trasmissione dell'informazione debbano essere rilevanti per il funzionamento dei neuroni reali. In effetti, quando D. MacKay e W.S. McCulloch (1952) hanno calcolato per la prima volta questi limiti, seguendo ipotesi diverse sulla struttura del codice neuronale, hanno manifestato cautela sulla rilevanza dei loro risultati. A mia conoscenza, questa è stata la prima applicazione della teoria dell'informazione al codice neuronaIe, pochi anni dopo il lavoro originale di Shannon; per una discussione più completa si veda il citato testo di Rieke e collaboratori (1997). Altri autori sono stati molto espliciti nell' esprimere l'opinione secondo la quale il cervello non potrebbe mai avvicinarsi al limite teorico, essendo vincolato da altri fattori. Così come il sistema visivo può contare i singoli fotoni o risolvere dettagli spaziali al livello imposto dalla diffrazione, anche il codice neuronale sembra avvicinarsi ai limiti fisici fondamentali.
Le rane e il loro richiamo
Noi viviamo in un mondo pieno di strutture, eppure la maggior parte degli esperimenti sul cervello prevede lo studio delle risposte a stimoli molto semplificati. Dagli etologi, d'altra parte, viene la tradizione di studiare animali che sono 'specialisti sensoriali': pipistrelli dotati della capacità di localizzare mediante l'eco, pesci con sensori elettrici, uccelli canori che imparano a riconoscere suoni complessi, e così via.
Parte del retroterra degli esperimenti su questi animali 'speciali' consiste nell' asserzione secondo la quale si dovrebbero studiare sistemi e compiti computazionali per i quali sia chiaro che si è avuta una selezione evolutiva volta a prestazioni elevate; il cervello non è un calcolatore privo di specializzazioni, ed è facile trovare compiti nei quali non dà buone prestazioni, per cui è interessante porsi domande sui compiti per i quali le prestazioni sono migliori. Questo richiede lo studio delle risposte dei neuroni agli stimoli che vengono effettivamente elaborati in condizioni naturali: i richiami ultrasonici dei pipistrelli, i canti di uccelli e così via. Un'idea connessa a questo approccio venne da H.B. Barlow, F.D. Attneave e altri, durante le prime formulazioni della teoria dell'informazione. Una formulazione chiara di questa idea si trova in Barlow (1961); per un'impostazione più moderna, si veda J.J. Atick (1992). Questi autori avanzarono l'ipotesi che il sistema nervoso, in particolare nei suoi primi stadi, potrebbe risultare adattato alla struttura statistica dei segnali naturali, così da poter fornire una rappresentazione particolarmente efficiente dei dati sensoriali naturali. Questa efficienza consentirebbe una rappresentazione più completa del mondo sensoriale utilizzando un numero limitato di neuroni o, più sottilmente, un numero limitato di impulsi. Si potrebbe così perfino sperare di promuovere questa nozione di efficienza allo status di principio: forse l'elaborazione dei segnali sensoriali porta a una rappresentazione all'interno del sistema nervoso che risulta ottimale e, in qualche modo, anche quantificabile sulla base della teoria dell'informazione. Si tratta di un'idea molto interessante, che sarà sviluppata nel seguito. Una conseguenza sperimentale ovvia di queste idee consiste nella possibilità di misurare la migliore efficienza con la quale vengono rappresentati gli stimoli di tipo naturale.
Il sistema uditivo della rana fornisce un banco di prova naturale per convalidare queste ipotesi. È possibile immaginare un insieme di stimoli completamente naturale: una registrazione su nastro deirichiami serali delle rane ottenuta in vicinanza di uno stagno. D'altro canto, è possibile costruire stimoli completamente casuali o non strutturati: un 'rumore bianco'. Tra questi due estremi, è possibile costruire insiemi che riflettono alcune, ma non tutte, I le strutture caratteristiche dei segnali casuali. Un primo, semplice passo consiste nel modellare il contenuto in frequenza, ovvero lo spettro di potenza degli stimoli, in modo che questi abbiano le stesse caratteristiche medie dei richiami delle rane. Si può andare oltre, incorporando non solo questa struttura spettrale (che corrisponde, approssimativamente, al tono e al timbro), ma anche alcune strutture temporali (le fluttuazioni ritmiche di intensità sonora) e alcune correlazioni precise tra diverse bande di frequenza, che portano, alla fine, al suono naturale della rana. Sorprendentemente, negli esperimenti di F. Rieke e collaboratori (1995) si osservò che già la prima fase, consistente nel formare lo spettro di potenza dei suoni, aveva un profondo effetto sull' efficienza della codifica da parte delle cellule nell' orecchio della rana.
Registrando da neuroni singoli nel nervo uditivo della rana (il fascio di cellule che porta informazione dall'orecchio al cervello) Rieke e collaboratori hanno utilizzato i metodi di ricostruzione sopra descritti per decodificare le sequenze di impulsi che derivano dal 'rumore bianco' o dagli stimoli 'di forma naturale'. In tutte le cellule studiate, le sequenze di impulsi trasferivano più informazione sui segnali di tipo naturale. Il tasso di informazione trasmessa poteva crescere anche quando le frequenze degli impulsi diminuivano, dimostrando che questo risultato non è spiegabile solo sulla base del fatto che le cellule rispondono più intensamente agli stimoli di tipo più naturale. l neuroni sono dunque capaci di utilizzare gli impulsi in modo più efficiente in risposta a stimoli naturali, almeno nel senso in cui viene trasmessa una quantità maggiore di informazione con un numero minore di impulsi. È possibile rendere quest'affermazione, così vicina alle ipotesi originali di Attneave e Barlow, un po' più precisa?
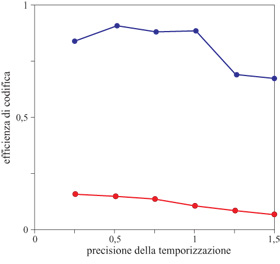
Come precedentemente osservato, l'entropia delle risposte neuronali fissa un limite alla capacità del neurone di trasmettere informazione. Questa entropia dipende dalla risoluzione temporale usata dagli sperimentatori (o dagli altri neuroni nel cervello della rana) per osservare la sequenza di impulsi, e quindi, per confrontare entropia e informazione, occorre passare in rassegna un intervallo di possibili risoluzioni temporali. La figura (fig. 3) mostra l'efficienza di codifica (cioè il rapporto tra informazione ed entropia) per una delle cellule dell' esperimento sulle rane, da cui si vede che, formando lo spettro dei suoni in modo da renderlo simile a quello del richiamo naturale della rana, si ha un effetto enorme sull' efficienza della codifica, in tutto un intervallo ragionevole di risoluzioni temporali. In questo caso l'efficienza della codifica raggiunge il 90% quando la rana ascolta i suoni più simili a quelli naturali, per cui si ha un utilizzo quasi perfetto della capacità della cellula per i segnali naturali, ma non per quelli casuali.
Gli esperimenti sulle rane, basati sulla determinazione dello spettro di potenza, sono solo un primo passo. C'è chiaramente un intero programma di ricerca necessario per colmare il vuoto tra gli stimoli semplificati o casuali, che sono stati gli strumenti tradizionali in neurobiologia, e i segnali più complessi e strutturati, quali quelli che incontriamo in natura. La difficoltà maggiore è determinata dalla scarsità degli strumenti utili per analizzare le risposte neuronali a segnali più naturali; in questo risiede uno degli aspetti più interessanti dell'approccio basato sulla ricostruzione dello stimolo, sebbene sia anch'esso soggetto a importanti limitazioni. Questa connessione tra la codifica neuronale e gli stimoli naturali è uno dei primi casi in cui le idee tratte dalla teoria dell'informazione sono state introdotte nello studio del cervello, anche se in modo qualitativo, da Attneave e Barlow. Spero che dagli esperimenti descritti sia risultato chiaro che la teoria dell'informazione fornisce il linguaggio quantitativo naturale per confrontare le risposte neuronali a segnali provenienti da insiemi molto diversi, fornendo gli strumenti matematici precisi con cui integrare l'intuizione dell'etologo.
Segnali visivi del movimento nella mosca
Se si osserva volare una mosca in una stanza, o all'aperto, si noterà che i percorsi di volo consistono per lo più in segmenti abbastanza rettilinei, interrotti da curve improvvise. È possibile quantificare queste osservazioni, sia misurando le traiettorie di volo, sia tramite esperimenti in cui la mosca viene sospesa a una bilancia di torsione (Heisenberg e Wolf, 1984). Considerando il comportamento aerodinamico applicabile a un oggetto delle dimensioni di una mosca, anche il volo rettilineo non è facile. Con la bilancia di torsione, si può dimostrare direttamente che il momento della forza è determinato dal movimento attraverso il campo visivo, e il segno è tale da stabilizzare il volo della mosca, che può essere assimilata a un corpo rigido soggetto a rotazioni. Ciò può essere dimostrato creando un meccanismo di retroazione, e cioè misurando il momento della forza e usando questo valore per ruotare in senso inverso lo stimolo visivo. Si è così realizzato un imperfetto simulatore di volo, in cui l'unica guida per il volo della mosca è di tipo visivo; in effetti, in condizioni naturali, anche i sensori meccanici della mosca giocano un ruolo cruciale. Malgrado le imperfezioni del simulatore di volo, la mosca legata fisserà gli oggetti piccoli, stabilizzandosi così su un volo all'apparenza rettilineo verso l'oggetto. La combinazione di esperimenti con volo libero e con la bilancia di torsione (ovvero col simulatore di volo) sostiene fortemente l'ipotesi che la mosca possa stimare la sua velocità angolare in base alle sole informazioni visive, e produrre quindi stimoli motori basati su tale stima (Reichardt e Poggio, 1976). L'anatomia quasi cristallina del cervello visivo della mosca ha permesso di identificare un piccolo gruppo di cellule che sembrano generare la codifica dei segnali visivi del movimento. In questo saggio non è possibile illustrare adeguatamente lo splendido lavoro anatomico e fisiologico che ha ottenuto questi risultati e che ha aperto la strada all'analisi discussa più oltre; per una rassegna di questi esperimenti con una estesa ricostruzione storica, si veda il libro curato da D.G. Stavenga e R.C. Hardie (1989). Una delle cellule individuate, il neurone Hl, è stata oggetto di diversi esperimenti dedicati a un'analisi quantitativa della trasmissione dell'informazione, e questo sistema ha fornito un banco di prova per lo sviluppo di varie e innovative tecniche di analisi, compresi i citati metodi di ricostruzione dello stimolo.
Nella figura (fig. 4) è mostrato un esempio degli esperimenti sul neurone Hl, basati sulla ricostruzione dello stimolo. La mosca vede scorrere una sequenza di immagini, ciascuna delle quali è costituita da barre verticali disposte in modo casuale e il cui moto procede rigidamente in direzione orizzontale. Poiché la sequenza viene vista solo da una porzione dell'occhio composto della mosca, questo movimento simula ciò che la mosca vedrebbe volando in modo irregolare lungo una linea retta. La velocità varia nel tempo in modo irregolare, come accadrebbe durante il movimento rotazionale della mosca in volo. Il neurone Hl, che è sensibile a questo movimento orizzontale, genera un numero di impulsi maggiore per il movimento in una direzione, e minore nell' altra. Se si esaminano in dettaglio le sequenze di impulsi, si può osservare che anche i singoli impulsi sono più o meno strettamente agganciati a brevi tratti di traiettoria. L'idea alla base della ricostruzione dello stimolo consiste nell'effettuare una stima dell'intera traiettoria, connettendo fra loro i brevi segmenti codificati dai singoli impulsi. Anche se non perfette, le ricostruzioni risultano molto accurate. La sequenza di impulsi può essere decodificata con una precisione di 0,1° di spostamento angolare, in finestre temporali di circa 30 ms, che rientrano nella scala di tempo utile per la maggior parte dei comportamenti della mosca. Questo livello di precisione è sorprendente, tenuto conto che il reticolo dei recettori e delle lenti nell'occhio composto della mosca sottende un'apertura angolare maggiore di 1°. È quindi possibile ricostruire il movimento su una scala dieci volte più piccola di quella caratteristica del campionamento dei pixel delle immagini d'ingresso. Inoltre, questa precisione è circa dieci volte migliore rispetto alla scala dell"offuscamento visivo' dovuto agli effetti di diffrazione ottica introdotti dalle lenti dell' occhio composto della mosca.
Come nel caso della cellula Hl della mosca, anche noi siamo in grado di valutare spostamenti molto più piccoli rispetto al 'limite di diffrazione' nominale, o alla separazione dei recettori nella nostra retina. Vi sono diversi fenomeni percettivi nei quali questa elevata precisione è rilevante e a essi si dà il nome di iperacuità (Westheimer, 1981). Gli esperimenti sul neurone Hl sono interessanti, perché forniscono un esempio di iperacuità sia nel funzionamento di un singolo neurone, sia nel contesto di un problema di stima, e non, come è comune in studi di questo genere, in problemi di discriminazione nell'ambito della percezione umana. Ammesso il fatto che possano essere rilevati spostamenti al di sotto del pixel, ci si può ragionevolmente chiedere se esistano reali limiti alla percezione. In effetti, il vero limite è determinato dalla combinazione dell'offuscamento dovuto alla diffrazione, dal campionamento dei recettori e dal rumore presente nei recettori stessi. Tuttavia, dai citati esperimenti di de Ruyter van Steveninck e Laughlin risulta una caratterizzazione abbastanza completa di questo rumore, da cui è possibile calcolare i limiti fisici assoluti della percezione del movimento nella mosca. Il fatto notevole è che gli esperimenti di ricostruzione su Hl mostrano un'accuratezza molto vicina a questo limite fisico. Sebbene il tasso complessivo di trasmissione dell'informazione, in questi primi esperimenti, fosse meno sorprendente di quanto lo era per quelli sul grillo, l'accuratezza della ricostruzione dimostra che la mosca è in grado di effettuare una stima quasi ottimale del movimento dal complesso insieme dei segnali provenienti dai recettori dell' occhio composto: la rappresentazione del movimento in H l si avvicina alla massima precisione consentita dal rumore presente nei recettori, e questo rumore si avvicina al valore minimo consentito dall'arrivo casuale dei fotoni. La ricostruzione dello stimolo permette di decodificare l'intera sequenza di impulsi che codificano uno stimolo complesso e dinamico. Un obiettivo più modesto consiste nel chiedersi se si possa comprendere e quantificare l'informazione trasferita da una breve sequenza di impulsi, o persino da un singolo impulso (de Ruyter van Steveninck e Bialek, 1988). Una semplificazione diversa riguarda la discriminazione tra due stimoli simili, piuttosto che la ricostruzione di uno stimolo complesso (de Ruyter van Steveninck e Bialek, 1995). L'affidabilità della discriminazione dovrebbe dipendere dall'accuratezza della ricostruzione, mentre l'analisi dei legami fra diversi gruppi di impulsi e classi di stimoli molto eterogenei suggerisce l'esigenza di nuovi e più sofisticati algoritmi di ricostruzione. Questi diversi tipi di esperimenti non sono stati effettuati solo su Hl, ma anche in una varietà di altri sistemi (Rieke et al., 1997). Se ci si propone di esplorare i sistemi di codifica e di elaborazione in sistemi neuronali più complessi, è auspicabile che trovino risposta prima le domande più semplici, prima fra tutte quella relativa all'informazione trasportata da un singolo impulso.
Metodi indipendenti dal modello
Uno dei primissimi tentativi di misurare la trasmissione di informazione per mezzo di sequenze di impulsi neuronali fu il lavoro di G. Werner e V.B. Mountcastle (1965) sui recettori del tatto nella pelle della scimmia. Il loro esperimento era molto simile a quello originale di Adrian: gli stimoli, in quel caso le incisioni sulla pelle, venivano attivati e lasciati attivi per un lungo periodo, e la risposta del neurone veniva quantificata contando gli impulsi in una finestra temporale successiva alla comparsa dello stimolo. Werner e Mountcastle scelsero l'ampiezza delle incisioni in modo casuale e, nel corso dell' esperimento, stilarono una tabella delle probabilità congiunte dei conteggi N e delle ampiezze delle incisioni A. Da questa tabella potevano calcolare la quantità d'informazione sull'ampiezza fornita dal conteggio degli impulsi, semplicemente applicando l'equazione [2]. La cosa importante è che non era necessario formulare alcuna ipotesi semplificativa sulla corrispondenza tra lo stimolo e la risposta. La difficoltà sta nel fatto che potrebbero essere necessarie quantità enormi di dati per fornire stime affidabili delle distribuzioni di probabilità. Quest'analisi della risposta a un insieme discreto di segnali è stata effettuata in vari sistemi, dai recettori tattili della pelle studiati da Werner e Mountcastle, fino alla corteccia visiva. Uno dei risultati più importanti emersi da questi diversi esperimenti riguarda la dinamica delle risposte. B.J. Richmond, L. Optican e i loro collaboratori furono tra i primi a sottolineare che la dinamica della risposta neuronale, successiva alla comparsa di uno stimolo, può trasportare una quantità notevole di informazione. Questo gruppo di ricercatori ha prodotto una lunga serie di lavori, utilizzando metodi tratti dalla teoria dell'informazione, per caratterizzare i neuroni della corteccia visiva dei primati (Optican e Richmond, 1987; Richmond et al., 1987; Richmond e Optican, 1987). In seguito, A. Treves, E.T. Rolls, M.J. Tovee e altri hanno dimostrato che una frazione rilevante dell'informazione accessibile, per esempio, in una presentazione statica di un'immagine di 300 ms si può ottenere analizzando 50 ms, o anche solo 20 ms di risposta neuronale. Diversi approcci sperimentali sono descritti in Rolls e Tovee (1994) e Tovee e collaboratori (1993), mentre la discussione teorica è trattata da S. Panzeri e collaboratori (1996). In effetti, la possibilità di ottenere questi risultati era già implicita nel lavoro originale di Werner e Mountcastle. Come fanno i neuroni a codificare più stimoli dinamici? Nel mondo reale gli stimoli cambiano di continuo, e ciò rende necessario disporre di una reazione veloce; così, anche se i segnali statici vengono codificati in modo affidabile in brevi segmenti temporali della risposta neuronale, il sistema potrebbe in effetti essere progettato per trattare le condizioni dinamiche più naturali. l citati metodi di ricostruzione dello stimolo affrontano questo problema decodificando opportunamente l'informazione contenuta nelle sequenze di impulsi neuronali, al variare dei segnali sensoriali lungo traiettorie complesse. Tali metodi tuttavia richiedono la conoscenza a priori delle caratteristiche del segnale che vengono codificate in un particolare neurone, mentre la scelta di uno specifico algoritmo di ricostruzione limita l'informazione estraibile. Sarebbe invece interessante poter effettuare una misurazione della trasmissione di informazione senza alcuna ipotesi circa la struttura del codice, e in condizioni naturali per quanto riguarda gli stimoli. Se ciò fosse possibile, verrebbe realizzato un metodo sperimentale di riferimento per la comprensione del codice neuronale.
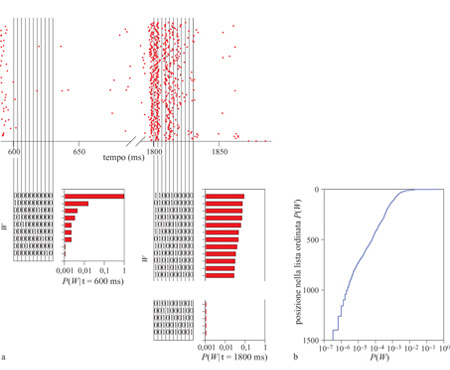
Negli esperimenti di Werner e Mountcastle, i diversi stimoli potevano essere classificati in base alle loro ampiezze. In un ambiente di complessi stimoli dinamici, tale classificazione può essere ottenuta usando la variabile tempo. Infatti, poiché lo stimolo varia nel tempo, la risposta neuronaIe può fornire un'informazione affidabile sullo stimolo stesso, a condizione che l'esperimento sia riproducibile sottoponendo una seconda volta al sistema uno stimolo con la stessa dipendenza temporale. Come mostrato in figura (fig. 5), questa intuizione può essere trasformata in una misurazione della trasmissione di informazione (de Ruyter van Steveninck et al., 1997; Strong et al., 1998). Per prima cosa, gli impulsi possono essere considerati come eventi che si presentano in intervalli discreti di tempo, cosicché un breve segmento tratto dalla sequenza di impulsi rappresenta una 'parola' con un numero limitato di 'lettere'. È anche possibile analizzare il caso di intervalli di dimensione variabile. Nel corso di un lungo esperimento è possibile accumulare la distribuzione delle parole usate dal neurone e, da questa distribuzione, determinare una certa entropia, dalla quale risulta fissato un valore massimo per l'informazione che il neurone può trasmettere. Ripetendo lo stesso stimolo molte volte, cioè mostrando alla mosca la stessa sequenza temporale di immagini mentre vengono registrati gli impulsi dalla cellula Hl, è anche possibile accumulare la distribuzione delle parole utilizzate quando si presenta lo stesso stimolo. La variabilità nell'uso delle parole in un certo istante rappresenta un rumore nella risposta, che può essere quantificato tramite l'entropia della distribuzione delle parole sulle varie ripetizioni. Inoltre, questa entropia del rumore è diversa nei differenti segmenti della sequenza di immagini, ma, mediando sul tempo e sottraendo all' entropia totale, è possibile ottenere l'informazione che la risposta neuronale fornisce sullo stimolo sensoriale. Esaminando segmenti sempre più lunghi della sequenza di impulsi, l'informazione e l'entropia tendono a crescere linearmente con il tempo, per cui si può parlare di un tasso ben definito al quale la cellula trasmette informazione.
Il punto chiave di questa analisi è che essa non dipende da alcuna ipotesi sulla struttura del codice neuronale. Dunque, si può misurare quanta informazione sullo stimolo viene fornita dagli impulsi, senza sapere in anticipo cosa, di quello stimolo, sia codificato da una specifica cellula. Si può inoltre indagare sulla dipendenza della trasmissione dell'informazione dai dettagli della sequenza di impulsi, che appaiono soltanto esaminando la sequenza a livelli sempre maggiori di risoluzione temporale, senza fare ipotesi su cosa essi possano rappresentare. Pertanto, se si analizza la risposta neuronale suddividendo il tempo in intervalli di durata ∆t, si ottiene che, al diminuire di ∆t, cioè all'aumentare della risoluzione temporale, l' entropia della risposta neuronaIe aumenta; il problema di determinare se la dettagliata risoluzione temporale degli impulsi è importante per la codifica si traduce nella questione se l'aumentata capacità di trasferire informazione sarà utilizzata effettivamente dalla cellula. Per il neurone Hl, almeno in un certo insieme di condizioni, il risultato è molto chiaro: in un ampio intervallo di risoluzioni temporali, da ∆t = 800 ms fino a ∆t = 2 ms, ogni bit supplementare di capacità di codifica (entropia) viene utilizzato per trasmettere informazione sulla traiettoria del movimento nel campo visivo, con efficienza quasi del 50%. In realtà, questi risultati (Strong et al., 1998) non mettono ancora in luce se i limiti della risoluzione temporale siano stati raggiunti. Sembra non esserci una singola scala caratteristica per la risoluzione temporale, e alcuni eventi nello stimolo sono rappresentati da impulsi, o gruppi di impulsi, riproducibili con un'accuratezza inferiore al millisecondo.
La separazione tra le misure dell'informazione e le ipotesi sulla struttura del codice appaiono particolarmente importanti non appena consideriamo l'analisi delle regioni più complesse del cervello. Per esempio, il lavoro di G. Buracas e collaboratori (1998) descrive l'applicazione di questi metodi diretti di misurazione dell'informazione allo studio della codifica del movimento visivo da parte delle cellule corticali dei primati, mentre M.J. Berry, D.K. Warland e M. Meister (1997) hanno utilizzato queste idee per analizzare in termini quantitativi la codifica delle sequenze dinamiche di immagini naturali da parte della retina dei vertebrati. In un lavoro tuttora in corso, Meister e i suoi collaboratori hanno studiato il modo in cui l'informazione trasmessa dalle cellule gangliari della retina possa essere suddivisa in contributi temporali di gruppi o raffiche di impulsi, in relazione al numero e alla temporizzazione precisa all'interno di ciascuna raffica. Anche in questo caso, è cruciale avere a disposizione metodi diretti per effettuare l'analisi, in modo da poter appurare la possibilità che caratteristiche diverse della risposta neuronale trasmettano quantità diverse di informazione, a prescindere da qualsiasi ipotesi (non ancora accertata) su cosa queste caratteristiche possano codificare. In questo ambito, Brenner è riuscito a quantificare l'informazione associata a singoli eventi nella risposta neuronale, siano essi singoli impulsi, gruppi di impulsi o anche impulsi coincidenti di diversi neuroni. Anche in questo caso l'analisi viene condotta semplicemente confrontando le variazioni nel tempo con le variazioni nelle ripetizioni dello stesso stimolo; tutto ciò senza alcuna ipotesi sulla struttura del codice.
Queste misurazioni dirette, o oggettive, della trasmissione dell'informazione fissano un riferimento sperimentale per la comprensione del codice neuronale. La possibilità di misurare il contenuto informativo dei singoli impulsi, e l'individuazione delle caratteristiche specifiche del mondo sensoriale a essi associate, permettono di calcolare l'informazione che gli impulsi forniscono su tali caratteristiche, e di dimostrare che questa è la totalità (o quasi) dell' informazione complessiva misurata in modo oggettivo. Analogamente, se è veramente possibile interpretare correttamente la lettura del codice, l'informazione estratta dall'analisi della ricostruzione dello stimolo dovrebbe essere pari all'informazione misurata, ottenuta con il metodo dell'analisi della riproducibilità e della variabilità delle 'parole', come indicato nella figura 5. Un confronto approfondito fra queste diverse misure di informazione permetterebbe di comprendere il codice in modo profondo e preciso: la sequenza degli impulsi fornisce una certa quantità di informazione sul mondo sensoriale, questa informazione è concentrata in certe caratteristiche dello stimolo e noi possiamo leggere tutta l'informazione ivi contenuta. Attualmente non c'è alcun sistema per il quale si sia potuto o si possa dire di possedere una simile comprensione completa, per quanto l'analisi del neurone Hl si avvicini molto a questo obiettivo.
Vecchi sogni rivisitati
È ora possibile focalizzare il contributo fornito dalla teoria dell'informazione all'analisi degli esperimenti sul sistema nervoso. Se da un lato i risultati sono ancora frammentari e ogni sistema ha le sue peculiarità, emergono alcune generalizzazioni, che saranno oggetto di ulteriori verifiche nei prossimi anni. In breve, la codifica dell'informazione da parte dei neuroni sensoriali è davvero efficiente, nel senso precisato dalla teoria dell'informazione. l singoli impulsi possono trasferire grandi quantità di informazione, i tassi di trasmissione dell'informazione sono vicini ai limiti imposti dall' entropia della sequenza di impulsi o dalla 'quantizzazione' in vescicole nelle sinapsi chimiche, e la precisione con cui le caratteristiche dello stimolo vengono codificate in profondità nel cervello è limitata dalle sorgenti fisiche di rumore dell'input sensoriale. È provato che gli stimoli più simili a quelli naturali sono codificati in modo più efficiente, e in generale nessuno dei risultati attuali sulla trasmissione di informazione e sulla efficienza della codifica si sarebbe potuto ottenere senza studiare le risposte neuronali a stimoli dinamici più complessi. Questi risultati avvalorano le idee di Attneave e Barlow, secondo cui le proprietà di risposta dei neuroni sarebbero ottimizzate proprio in vista di una codifica efficiente dei segnali naturali. C'è un sogno, che emerge da questi vecchi lavori, per cui i principi di ottimizzazione basati sulla teoria dell'informazione potrebbero fornire una vera teoria, e non solo un modello parametrizzato, per l'elaborazione sensoriale di base, e non c'è dubbio che l'analisi sperimentale della codifica efficiente fornisce il massimo sostegno possibile ai tentativi condotti in questa direzione.
È anche chiaro che ogni generalizzazione ingenua tratta dai risultati acquisiti sulla trasmissione dell'informazione e sulla efficienza del codice non può che essere errata: per esempio, mentre la retina può trasmettere informazione in modo efficiente, quando i segnali giungono alla corteccia visiva c'è un aumento enorme del numero dei neuroni che codificano il mondo visivo, e allora è difficile immaginare che la stessa nozione di efficienza sia ancora significativa. Questo però non vuoI dire che la teoria dell'informazione sia irrilevante per lo studio della corteccia. Infatti, in primo luogo, ciò che è ora noto sulla trasmissione dell'informazione nei neuroni sensoriali è stato ottenuto solo introducendo modifiche rilevanti all'impostazione degli esperimenti, mentre non è ancora noto ciò che tale impostazione permetterà di apprendere quando sarà applicata all'analisi di aree cerebrali più complesse.
In secondo luogo, la teoria dell'informazione può essere validamente utilizzata per precisare idee sul codice, sulla selettività e così via. Anche se le risposte possono essere diverse per aree diverse del cervello, le domande di base sono le stesse, e dagli esperimenti recenti sui neuroni sensoriali risulta che l'approccio basato sulla teoria dell'informazione fornisce strumenti utili per la formulazione corretta di queste domande. Inoltre, se da un lato è difficile sostenere che il codice corticale possa essere efficiente nello stesso senso di quello sensoriale periferico, dall'altro è anche difficile immaginare che i segnali, molto precisi, trasmessi dai neuroni sensoriali, siano semplicemente riversati senza alcun criterio, e come in una 'zuppa di rumori', nella corteccia: la scoperta che alcuni neuroni possono fungere da elementi molto precisi per la trasmissione e l'elaborazione dell'informazione induce a ricercare cos'è che fa apparire altri neuroni poco precisi o inefficienti. Infine, e questa è una questione più profonda, è possibile che i principi che governano le funzioni cerebrali superiori siano parimenti ben radicati nella teoria dell'informazione, ma che, al tempo stesso, siano diversi da quelli che presiedono alla codifica sensoriale. Per esempio, H.E. Barlow ha sottolineato come esista una nozione assoluta di efficienza per l'apprendimento in un ambiente rumoroso o probabilistico, e che sarebbe interessante misurare l'efficienza dell'apprendimento da parte di esseri umani o di animali nello stesso modo in cui misuriamo l'efficienza del conteggio dei fotoni nella retina, o quella della trasmissione dell'informazione da parte dei neuroni sensoriali. Per concludere, le misure della trasmissione dell'informazione da parte di neuroni reali hanno gettato luce su un aspetto del funzionamento del cervello, cioè la rappresentazione di segnali dinamici per mezzo di sequenze di impulsi. Si può dire che si è sul punto di comprendere in modo completo questa rappresentazione in alcuni dei casi più semplici. Se è vero che il grande sogno degli anni Cinquanta è molto lontano, il tentativo di misurare la trasmissione dell'informazione nel sistema nervoso ha stimolato molti nuovi esperimenti quantitativi, e lungo questa strada molte cose sono state apprese. Questi sforzi hanno riportato in primo piano vecchie questioni sull'affidabilità dei neuroni e dell'elaborazione neuronale. Il fondamento stesso di un approccio basato sulla teoria dell'informazione (cioè il fatto che i segnali sensoriali siano tratti da una distribuzione di probabilità) ha incoraggiato gli sforzi per caratterizzare la distribuzione dei segnali nel mondo reale, e per progettare esperimenti che approssimino meglio questa distribuzione naturale. Ragionando in termini di distribuzione di stimoli, è chiaro che i neuroni possono adattarsi non solo a semplici medie, come nell'adattamento alla luce e all'oscurità, ma all'intera struttura statistica dell'insieme degli stimoli; a questo riguardo si sta accumulando una serie di prove di questo 'adattamento alla statistica'. Si sta anche esaminando la possibilità di comprendere in generale l'adattamento nel senso di un avvicinamento verso un codice più efficiente, per esempio, dopo un cambiamento improvviso dell'ambiente.
Infine, la teoria dell'informazione consente di stabilire, in linea di principio, un ponte concettuale tra il problema del codice e dell'affidabilità, affrontato a livello del singolo neurone, e i problemi apparentemente più astratti di inferenza e apprendimento, inerenti alle grandi reti delle aree cerebrali superiori. Resta da vedere se questa connessione, che rinnoverebbe davvero i grandi sogni del passato, sia realmente possibile.
Bibliografia citata
ATICK, J.J. (1992) Could information theory provide an ecological theory of sensory processing? In Princeton lectures on biophysics: NEC Research Institut, Princeton USA, 23-29, June 1991, a c. di Bialek W., Singapore, River Edge, NT, World Scientific, pp. 223-289.
BARLOW, H.B. (1961) Possible principles underlying the transformation of sensory messages. In Sensory communication, contributions, Symposium on Principles of Sensory Communication, 1959, Endicott House, a c. di Rosenblith W., Cambridge, Mass., MIT Press, pp. 217-234.
BERRY, M.J., WARLAND, D.K., MEISTER, M. (1997) The structure and precision of retinal spike trains. Proc. Natl. Acad. Sci. USA, 94, 5411-5416.
BIALEK, W., ZEE, A. (1990) Coding and computation with neural spike trains. J. Stat. Phys., 59, 103-115.
BIALEK, W., RIEKE, F., DE RUYTER VAN STEVENINCK, R., WARLAND, D. (1991) Reading a neural code. Science, 252, 1854-1857.
BURACAS, G., ZADOR, A., DE WEESE, M., ALBRIGHT, T. (1998) Efficient discrimination of temporal patterns by motion sensitive neurons in primate visual cortex. Neuron, 20, 959-969.
HEISENBERG, M., WOLF, R. (1984) Vision in Drosophila: genetics oJmicrobehavior. Berlino-New York, Springer Verlag.
MAcKAY, D., McCULLOcH, W.S. (1952) The limiting information capacity ofa neuronallink. Bull. Math. Biophys., 14, 127-135.
NARINS, P.M., LEWIS, E.R. (1984) The vertebrate ear as an exquisite seismic sensor. J. Acoust. Soc. Am., 76, 1384-1387.
OPTICAN, L.M., RICHMOND, B.J. (1987) Temporal encoding of two-dimensional patterns by single units in primate inferior temporal cortex. III: Information theoretic analysis. J. Neurophysiol., 57,162-178.
PANZERI, S., BIELLA, G., ROLLS, E.T., SKAGGS, W.E., TREVES, A. (1996) Speed, noise, information and the graded nature of neuronal responses. Network, 7, 365-370.
REICHARD, W., POGGIO, T. (1976) Visual control of orientation behaviour in the fly. Part I: A quantitative analysis. Q. Rew. Biophys., 9, 311-375.
RICHMOND, B.J., OPTICAN, L.M. (1987) Temporal encoding oftwo dimensional patterns by single units in primate inferior temporal cortex. II: Quantification of response waveform. J. Neurophysiol., 57, 147-161.
RICHMOND, B.J., OPTICAN, L.M., PODELL, M., SPITZER, H. (1987) Temporal encoding of two-dimensional patterns by single units in primate inferior temporal cortex. I: Response characteristics. J. Neurophysiol., 57, 132-146.
RIEKE, F., BAYLOR, D.A. (1998) Single photon detection by rod cells ofthe retina. Revs. Mod. Phys., 70,1027-1036.
RIEKE, F., BODNAR, D.A., BIALEK, W. (1995) Naturalistic stimuli increase the rate and efficiency of information transmission by primary auditory afferents. Proc. R. Soc. Lond. B Biol. Sci., 262, 259-265.
RIEKE, F., WARLAND, D., DE RUYTER VAN STEVENINCK, R., BIALEK, W. (1997) Spikes: exploring the neural code. Cambridge, Mass., MIT Press.
ROLLS, E.T., TOVEE, M.J. (1994) Processing speed in the cerebral cortex and the neurophysiology of visual masking. Proc. R. Soc. Lond. B Biol. Sci., 257, 9-15.
DE RUYTER VAN STEVENINCK, R., BIALEK, W. (1988) Real-time performance of a movement sensitive neuron in the blowfly visual system: coding and information transfer in short spike sequences. Proc. R. Soc. Lond. B Biol. Sci., 234, 379-414.
DE RUYTER VAN STEVENINCK, R., BIALEK, W. (1995) Reliability and statistical efficiency of a blowfly movement-sensitive neuron. Phil. Trans. R. Soc. Lond., 348, 321-340.
DE RUYTER VAN STEVENINCK, R., LAUGHLIN, S.B. (1996) The rate of information transfer at graded-potential synapses. Nature, 379, 642-645.
DE RUYTER VAN STEVENINCK, R., LEWEN, G.D., STRONG, S.P., KOBERLE, R., BIALEK, W. (1997) Reproducibility and variability in neural spike trains. Science, 275, 1805-1808.
SHANNON, C.E., WEAVER, W. (1949) The mathematical theory of communication. Urbana, University of Illinois Press.
STAVENGA, D.G., HARDIE, R.C., a c. di (1989) Facets of vision. Berlino-New York, Springer Verlag.
STRONG, S.P., KOBERLE, R., DE RUYTER VAN STEVENINCK, R., BIALEK, W. (1998) Entropy and information in neural spike trains. Phys. Rev. Lett., 80, 197-200.
TOVEE, M.J., ROLLS, E.T., TREVES, A., BELLIS, R.P. (1993) Information encoding and responses of single neurons in the primate temporal visual cortex. J. Neurophysiol., 70, 640-654.
WARLAND, D., LANDOLFA, M., MILLER, J.P., BIALEK, W. (1992) Reading between the spikes in the cercaI filiform hair receptors of the cricket. In Analysis and modeling of neural systems, a c. di Eeckman H., Boston, Kluver Academic Publishers, pp. 327-333.
WERNER, G., MUUNTCASTLE, V.B. (1965) Neural activity in mechanoreceptive cutaneous afferents: stimulus-response relations, Weber functions, and information transmission. J. Neurophysiol., 75, 2280-2293.
WESTHEIMER, G. (1981) Visual hyperacuity. Prog. Sens. Physiol., 1, 1-30.