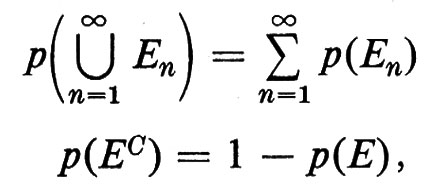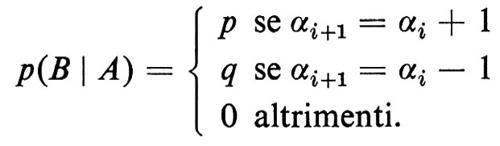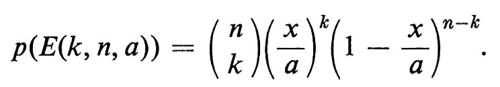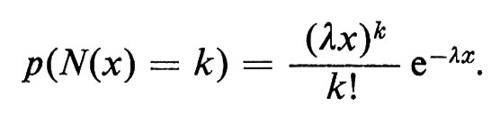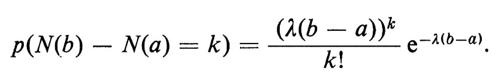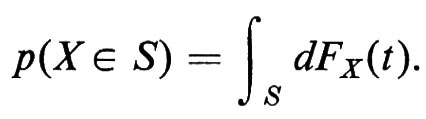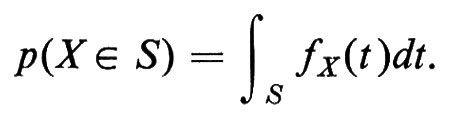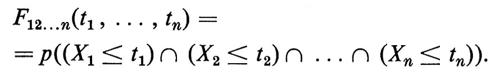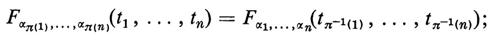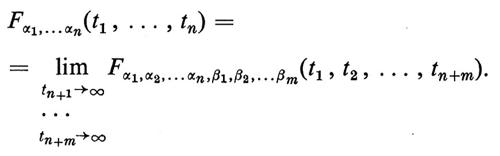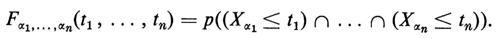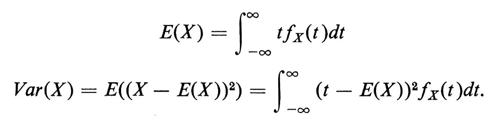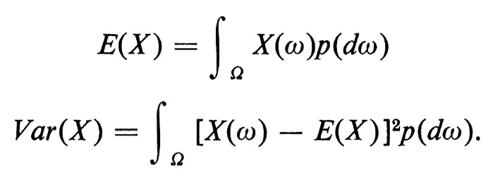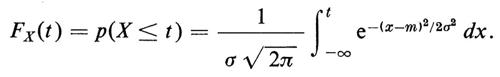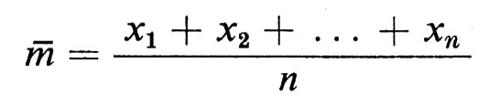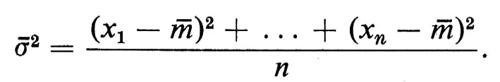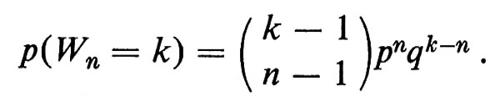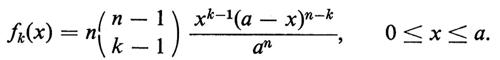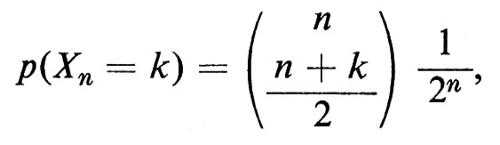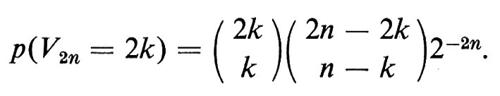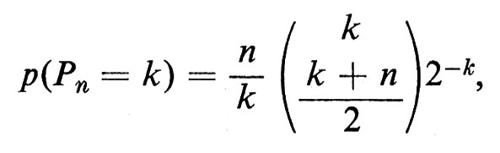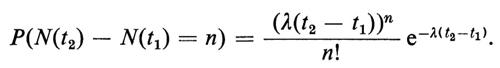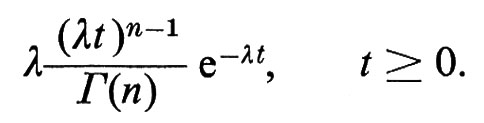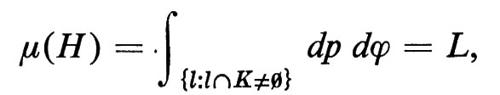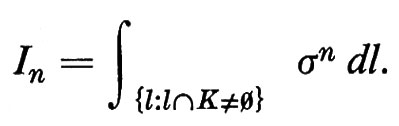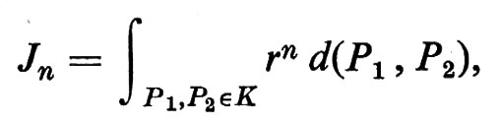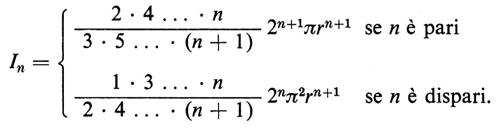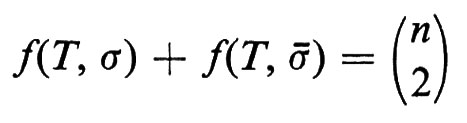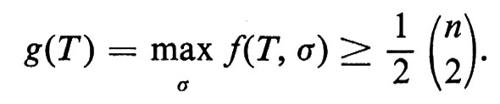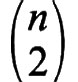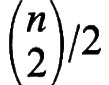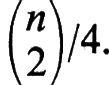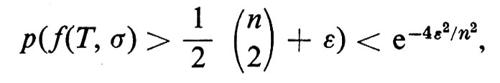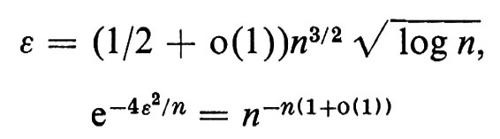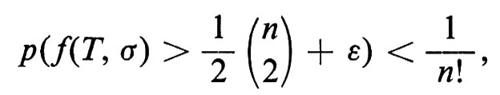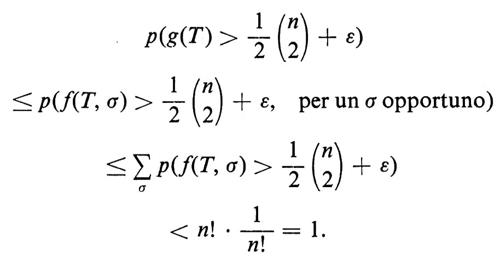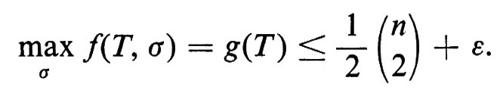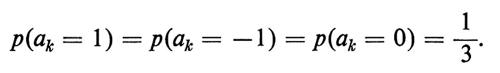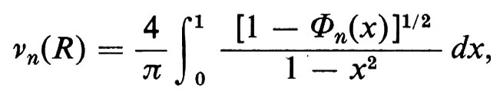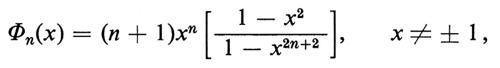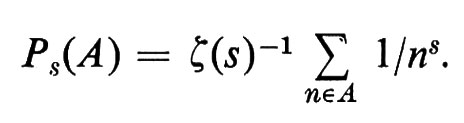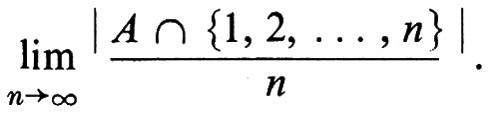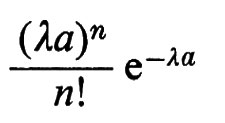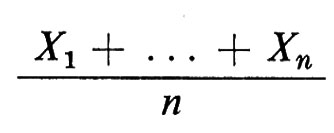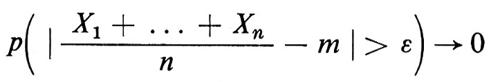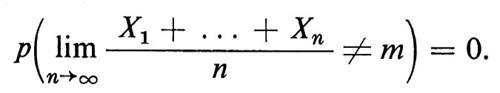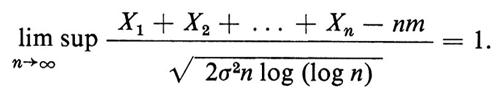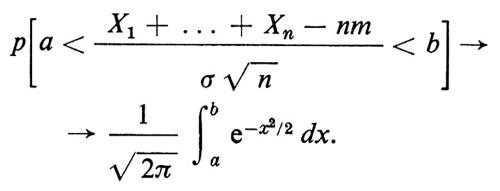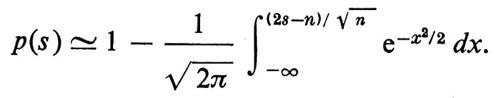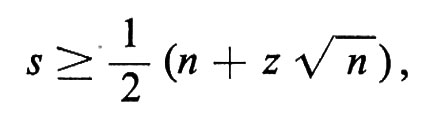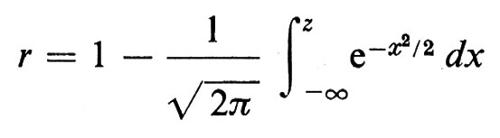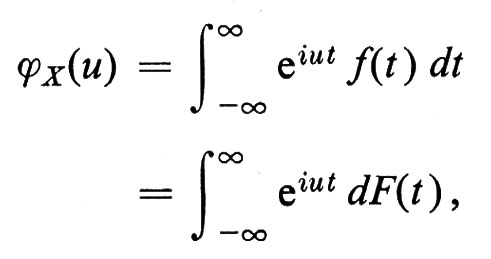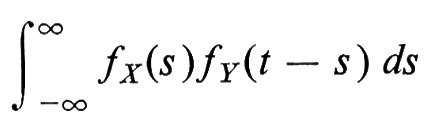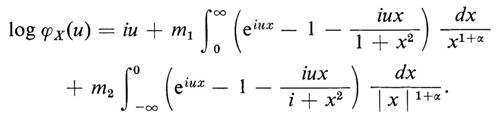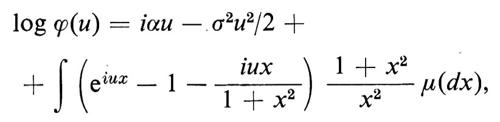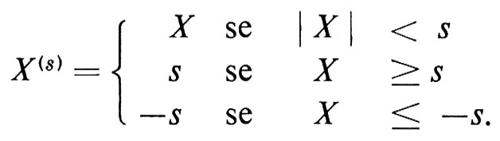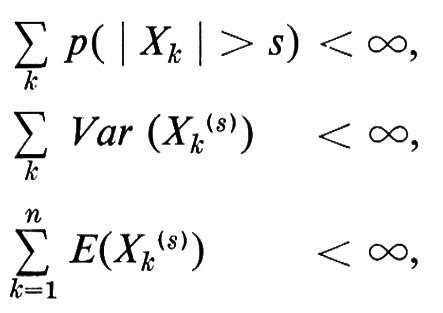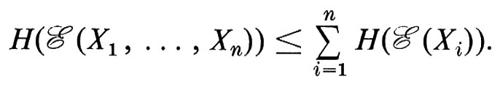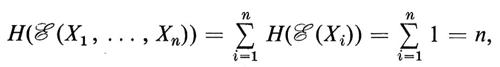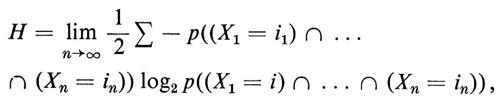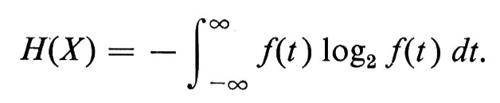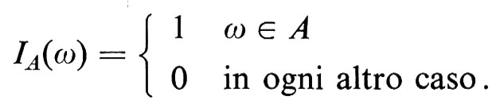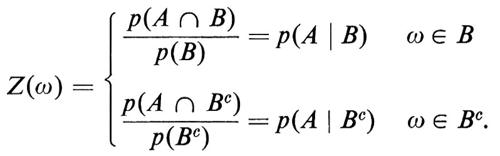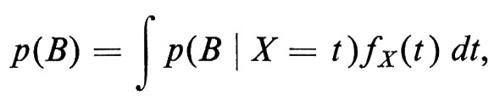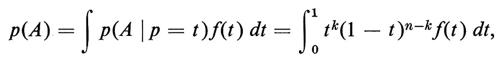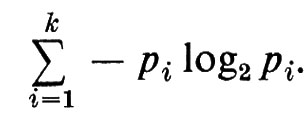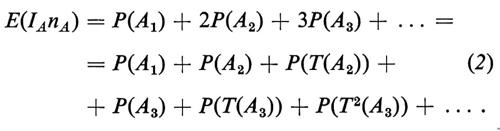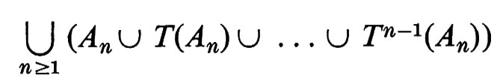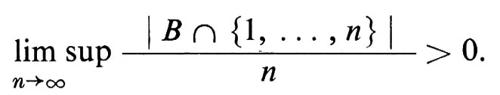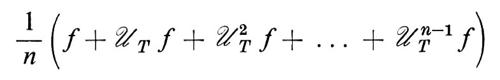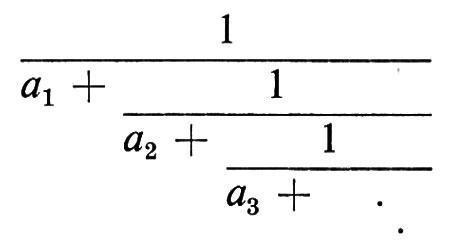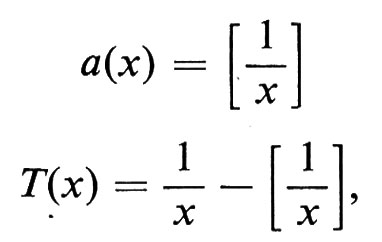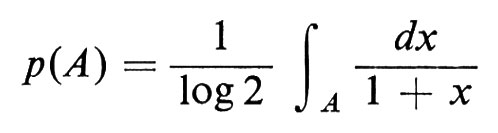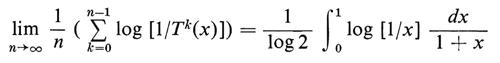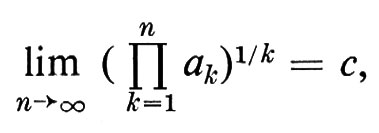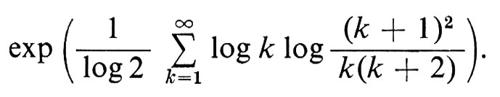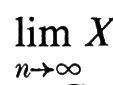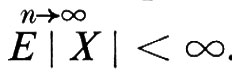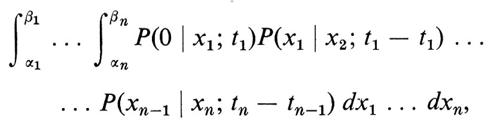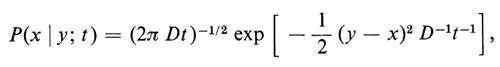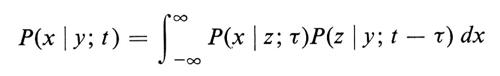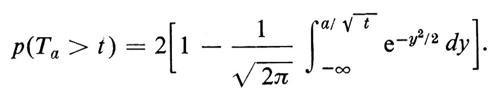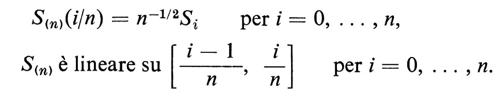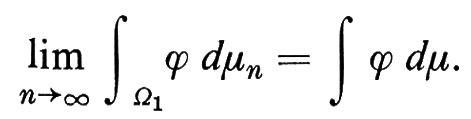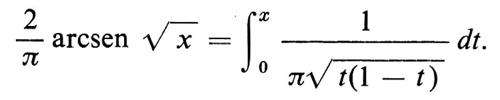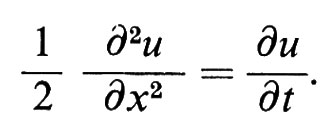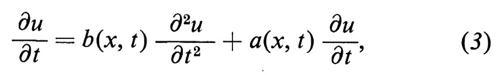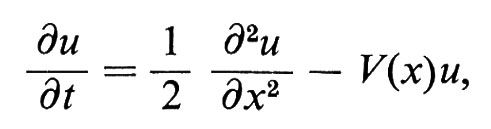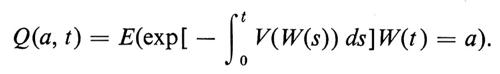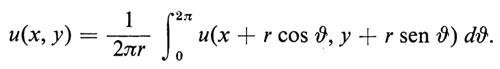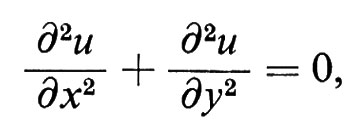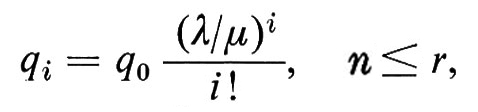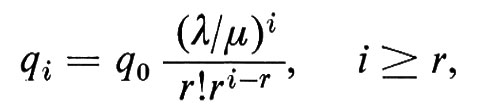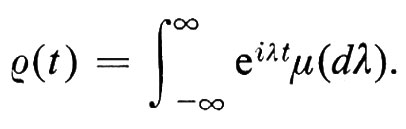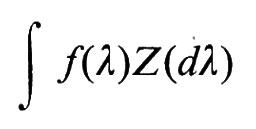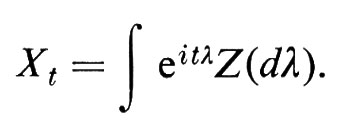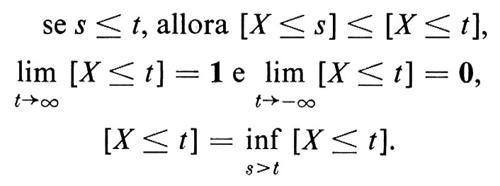Probabilita

Probabilità

*La voce enciclopedica Probabilità è stata ripubblicata da Treccani Libri, arricchita e aggiornata da un contributo di Marco Li Calzi.

sommario: 1. Introduzione. 2. Spazi campione.  3. Variabili casuali. 4. Natura del pensiero probabilistico. a) Geometria integrale. b)Teoria non costruttiva dei grafi. c) Zeri di polinomi casuali. d) Teoria dei numeri probabilistica. e) Distribuzione delle prime cifre. f) Accrescimento delle cellule. g) Monete su un tappeto. 5. Somme di variabili casuali indipendenti. 6. Probabilità condizionata. 7. Teoria ergodica e martingale. 8. Moto browniano. 9. Processi di Markov. 10. Processi gaussiani. 11. Fondamenti filosofici della probabilità. □ Bibliografia.

1. Introduzione

Il termine ‛probabilità', come i termini ‛geometria' o ‛algebra', non indica soltanto un determinato ramo della matematica, ricco di risultati profondi e di concetti penetranti. Proprio come la geometria, la probabilità è caratterizzata dal modo particolare in cui affronta i problemi matematici, qualunque sia la loro origine, e altresì dalla peculiare capacità dei suoi cultori di comunicare e di riconoscersi fra loro. La verità finale della teoria esula dall'ambito dell'esposizione matematica ordinaria.

Sotto certi aspetti, il ragionamento probabilistico è un ampliamento della logica classica. Fin dagli inizi, ha voluto essere una logica con un continuo di valori di verità, ma fino ad ora questa pretesa non ha avuto il sostegno di uno sviluppo sintattico simile a quello del calcolo dei predicati, per quanto alcuni recenti risultati della scuola di H. J. Keisler indichino finalmente i primi passi in quella direzione. Soltanto una certa familiarità con il ragionamento probabilistico mostra il vantaggio di stabilire, per esempio, l'esistenza di un oggetto matematico dimostrando che un oggetto siffatto esiste con probabilità positiva, oppure di sostituire l'enunciato di un problema estremamente arduo con un altro più debole ma dimostrabile, il quale affermi che l'enunciato iniziale è vero con probabilità 1.

Diversamente dalla geometria, che giunge a noi con una tradizione che impone il proprio stile - quello assiomatico-deduttivo ereditato da Euclide - come paradigma di ragionamento matematico, la probabilità ha sofferto per le sue origini relativamente recenti. Attraverso il lavoro pionieristico di Gauss - per ricordare solo i nomi più significativi - che osservò la natura primaria della distribuzione normale, di Poisson, che scoprì la distribuzione che oggi porta il suo nome, di Boole, che intuì la struttura algebrica soggiacente alla probabilità, e di Crofton, che, nella nona edizione della Encyclopaedia Britannica, sviluppò le idee di base della probabilità geometrica, lentamente, nel XIX secolo, la probabilità raggiunse la propria autonomia e attraversò una adolescenza agitata intorno al 1920. Non vi è dubbio che il più geniale e più influente probabilista di questo periodo giovanile fu P. Lévy, al cui spirito inventivo si devono gran parte delle idee della probabilità contemporanea. Soltanto verso il 1930, tuttavia, l'insegnamento della probabilità come disciplina indipendente venne finalmente accettato. Una tappa fondamentale in questo processo fu la pubblicazione del primo volume dell'ormai classico trattato di W. Feller An introduction to probability theory and its applications nel 1950. Sempre a causa della relativa giovinezza di questo campo è lecito prevedere che le attuali formulazioni della probabilità in termini desunti dalla teoria della misura dovranno essere riviste tenendo conto sia dei grossi problemi posti da diverse discipline scientifiche, come la teoria quantistica dei campi, la teoria della comunicazione, la biologia molecolare, sia, soprattutto, della necessità di statistiche più realistiche. Malgrado le penetranti analisi filosofiche sui fondamenti della statistica, compiute da Fr. Ramsey, B. De Finetti, J. Savage e R. A. Fisher, per citare solo alcuni, si può prevedere che le statistiche sofisticate richieste dalla scienza contemporanea porteranno con sé una rivoluzione nell'ambito della probabilità.

Attualmente, i ricercatori nel campo della probabilità si possono classificare in due scuole relativamente ben definite. La prima, e più antica, sottolinea l'intuitività e l'applicabilità del ragionamento probabilistico. I suoi luminari sono, o sono stati, W. Feller, J. M. Hammersley, M. Kac, P. Lévy, H. Kesten, H. P. McKean e S. M. Ulam, tanto per citarne alcuni. La seconda scuola, che è la più recente, utilizza le tecniche della teoria della misura e dell'analisi funzionale, a costo di rinunciare a una maggiore ampiezza per una presentazione più formale. Essa fu fondata in Russia, il solo paese con una tradizione ininterrotta in questo campo; risale a Čebyšev e porta alla memoria nomi come quelli di R. Chacon, K. L. Chung, J. L. Doob, R. Dudley, D. O. Kendall, A. Khintchine, J. F. C. Kingman, A. N. Kolmogorov, P. A. Meyer, J. Neveu, D. Ornstein, D. Ray e F. Spitzer, sempre per fare qualche nome soltanto. La differenza di stile fra queste due scuole appare evidente confrontando i due testi più rappresentativi della prima e della seconda rispettivamente: la Théorie de l'addition des variables aléatoires (Paris 1937) di P. Lévy e i Grundbegriffe der Wahrscheinlichkeitsrechnung di A. N. Kolmogorov (Berlin 1933).

2. Spazi campione

Esistono due modi di porre i concetti di base della moderna teoria della probabilità. Il primo si sviluppa a partire dalla nozione di evento in uno spazio campione, l'altro, basandosi su fondamenta fenomenologicamente più solide, prende le mosse dalla nozione di variabile casuale.

Storicamente la nozione di variabile casuale nacque molto più tardi, dopo la metà dell'Ottocento, dal concetto di evento. Forse proprio per questo, ancor oggi, la maggior parte dei metodi con cui si tratta la probabilità partendo dal concetto di spazio campione definisce una variabile casuale come una funzione su uno spazio campione.

Uno ‛spazio campione' (o spazio dei campioni) è un insieme Ω dotato di una struttura molto semplice. Intuitivamente, ogni punto in Ω rappresenta un possibile risultato di un dato esperimento. Certi sottoinsiemi di Ω, che formano una σ-algebra di Boole ℰ, vengono chiamati ‛eventi'. In tutti i casi particolari, la σ-algebra di Boole ℰ si ottiene specificando anzitutto certi eventi ‛elementari' e definendo quindi un evento come un elemento della ‛algebra di Boole generata da tali eventi elementari, e precisamente la più piccola famiglia di sottoinsiemi di Ω contenente gli eventi elementari e chiusa rispetto alle operazioni di unione numerabile e passaggio al complementare. Una probabilità è una funzione di insieme p numerabilmente additiva, che assume valori compresi tra 0 e 1, definita su ℰ. In simboli, data una qualunque collezione {E_n} in ℰ tale che, per ogni m ≠ n, E_m ⋂ E_n = 0/,

ove E^C è il complementare dell'insieme E. Si richiede inoltre che sia p(Ω) = 1. Per un dato evento E, il valore p(E) viene chiamato ‛la probabilità dell'evento E'.

Tra le diverse operazioni fra spazi campione, la più importante è il ‛prodotto'. Dati due spazi campione Ω₁ e Ω₂ con σ-algebre ℰ₁ e ℰ₂ misure di probabilità p₁ e p₂ sia Ω = Ω₁ × Ω₂ e denotiamo con ℰ la più piccola σ-algebra contenente ℰ₁ × ℰ₂. Definiamo anzitutto p su ℰ₁ × ℰ₂ ponendo, per E₁ ∈ ℰ₁ e E₂ ∈ ℰ₂,

p(E₁ × E₂) = p₁(E₁)p₂(E₂).

Estendiamo quindi questa definizione, nell'unico modo possibile, a tutti gli ℰ.

In modo simile si può definire il prodotto di un numero arbitrario (anche non numerabile) di spazi campione.

La nozione di prodotto di spazi campione rende rigorosa la nozione intuitiva di ‛indipendenza stocastica' (o, più brevemente, indipendenza), che, per accordo unanime, è l'idea fondamentale della teoria della probabilità (στόχος significa in greco ‛congettura'). Una famiglia ℱ di eventi si dice indipendente se, e soltanto se,

p(E_i1 ⋂ E_i2 ⋂ . . . ⋂ E_ik) = p(E_i1)p(E_i2) . . . p(E_ik),

per ogni sottoinsieme finito E_i1, . . ., E_ik di eventi distinti nella famiglia ℱ. Se Ω = Ω₁ × Ω₂, i due eventi E₁ × Ω₂ e Ω₁ × E₂ sono indipendenti. Inversamente, ogni famiglia di eventi indipendenti può rappresentarsi in questo modo, esprimendo lo spazio campione dato come un prodotto.

Ecco alcuni esempi fondamentali di spazi campione.

1. Lo spazio campione di Bernoulli. - Lo spazio campione di Bernoulli viene utilizzato per lo studio del ‛lancio di una moneta'. Punti di questo spazio campione sono successioni infinite di 0 e 1, ciascuna delle quali corrisponde a una successione infinita di lanci di una moneta truccata, con probabilità p che venga testa e q che venga croce (con p + q = 1). Indicando con E_n l'evento elementare consistente nel fatto che si presenti testa all'n-esimo lancio, sia ℰ la σ-algebra generata dalla collezione {E_n} di eventi elementari. Supporremo che due eventi E_k ed E_n(k ≠ n) siano indipendenti e faremo un'ipotesi analoga per ogni insieme finito di E_i, ponendo inoltre p(E_n) = p per ogni n. Questa definizione di p(E_n) si estende in modo unico a tutto ℰ. Lo spazio campione risultante è stato oggetto di un'indagine molto estesa. Per quanto possa sembrare estremamente semplice, il fenomeno del lancio della moneta presenta aspetti sottili e paradossali e solo in anni recenti alcuni di questi aspetti sono venuti alla luce. Da questo esempio si può intravedere come la nozione intuitiva di indipendenza di lanci successivi di una moneta possa essere resa precisa da metodi di teoria della misura.

2. Lo spazio campione uniforme. - L'insieme degli eventi è la famiglia ℰ di tutti i sottoinsiemi misurabili secondo Lebesgue dell'intervallo [0,a] = Ω e p(E) è la misura normalizzata di Lebesgue di E. Borel fu il primo a usare l'isomorfismo tra l'intervallo [0,1] e lo spazio campione di Bernoulli con p = q = 1/2, che si ottiene associando a ogni successione infinita di 0 e di 1 il numero reale in [0,1] che ha tale successione di 0 e di 1 come sua rappresentazione binaria. L'esperimento di scegliere n punti a caso nell'intervallo [0,a] viene studiato mediante lo spazio campione prodotto di n copie dello spazio campione uniforme.

3. Passeggiate aleatorie. - Dal punto di vista fenomenologico, una passeggiata aleatoria è il processo stocastico secondo il quale un punto, o una ‛particella', si muove mediante piccoli salti, o in modo continuo, ‛a caso', su una data superficie. La casualità del moto è specificata dalla condizione che, una volta che la particella si trovi in un punto A della superficie, si stabilisca una probabilità per la lunghezza e la direzione secondo le quali avrà luogo il prossimo passo sulla superficie.

Per fissare le idee, consideriamo una particella che si muova sui punti di coordinate intere nel piano. Se la particella si trova in un punto (i, j), si danno quattro probabilità corrispondenti ai quattro punti di coordinate intere che circondano la particella e verso cui la particella può muoversi; se queste probabilità sono uguali, si dice che la passeggiata aleatoria è simmetrica. Si fa sempre l'ipotesi che la somma di queste quattro probabilità sia uguale a 1; inoltre accade sovente che tali probabilità siano indipendenti dal punto A e, in tal caso, si dice che la passeggiata aleatoria è omogenea.

Storicamente la definizione di spazio campione corrispondente a questo processo intuitivo emerse lentamente. Ne daremo ora la definizione per la passeggiata aleatoria unidimensionale, omogenea e non necessariamente simmetrica, di una particella che si muova verso destra con probabilità p e verso sinistra con probabilità q.

Lo spazio campione Ω e' la famiglia di tutte le successioni infinite a valori interi α = (α₀, α₁, α₂ ... .) tali che, per ogni i, ∣ α_i+1 − α_i ∣ = 1. Ogni siffatta successione infinita a descrive una possibile traiettoria per la particella e α₁ dà la posizione della particella dopo i passi. Indichiamo con E_n l'evento elementare consistente nel fatto che la particella all'n-esimo passo si muova da α_n verso α_n + 1; sia ℰ la σ-algebra generata dalla famiglia di eventi elementari {E_n}. Posto p(E_n) = p, supponiamo che ogni sottoinsieme finito di E_i consti di eventi indipendenti. Questa definizione di probabilità si estende in modo unico a tutta la σ-algebra ℰ generata dagli eventi elementari E_n. La posizione α_i al passo i in una passeggiata aleatoria può essere interpretata come il capitale di un giocatore che inizi a giocare con un capitale α₀ e giochi con una moneta truccata. Con ciò si stabilisce un isomorfismo tra lo spazio campione di una passeggiata aleatoria e lo spazio campione di Bernoulli. Questo isomorfismo può, in un certo senso, indurre in errore, in quanto gli analoghi continui di questi due spazi campione, rispettivamente il moto browniano e il processo di Poisson, sono profondamente diversi.

Il concetto di passeggiata aleatoria illustra l'idea fondamentale di ‛probabilità condizionata', la quale misura la dipendenza di un evento da un altro. La probabilità condizionata di un evento A una volta verificatosi l'evento B, indicata con p(A ∣ B), è definita dall'uguaglianza:

p(A ∣ B) = p(A ⋂ B)/p(B),

ovviamente a condizione che sia p(B) ⟨ 0.

Per esempio, se A e B sono indipendenti, p(A ∣ B) = p(A) e viceversa. Nel caso della nostra passeggiata aleatoria a una dimensione, se A è l'evento consistente nel fatto che la particella stia nella posizione α_i, all'i-esimo passo e B è l'evento consistente nel fatto che la particella stia nella posizione α_i+1 all'i + 1-esimo passo, risulta

4. Processi di Poisson. - Lo spazio campione di Poisson fornisce una base matematica formale allo studio di fenomeni di vario tipo, quali ad esempio quelli riferentisi all'accadere casuale di accidenti istantanei nel tempo (come il sopraggiungere di clienti in un negozio, chiamate telefoniche, ecc.), oppure fenomeni connessi a una distribuzione di punti su una superficie di area infinita, senza punti di accumulazione e sotto la condizione, che preciseremo tra poco, che il numero di punti che cadono nell'unità di area sia una costante λ, chiamata densità o intensità del processo.

Per fissare le idee, consideriamo la semiretta [0, ∞). Lo ‛spazio campione di Poisson' Ω è, in questo caso, la famiglia di tutti i sottoinsiemi di [0, ∞) privi di punti di accumulazione, cioè di tutti i sottoinsiemi di [0, ∞) contenenti al più un numero finito di punti in ogni intervallo limitato (a, b). Gli eventi elementari sono indicati con (N(b) − N(a) = k) - giustificheremo tra poco questa notazione - e consistono di tutti gli elementi di Ω che hanno esattamente k punti nell'intervallo (a, b). Sia ℰ la σ-algebra generata da questi eventi elementari. Imponiamo la condizione che due (o più) eventi elementari

(N(b) − N(a) = k) e (N(d) − N(c) = m)

siano indipendenti ogniqualvolta (a, b) ⋂ (c, d) = 0/; questa condizione equivale a dire che i punti che compaiono in intervalli disgiunti sono eventi indipendenti. È interessante notare come, nella teoria della probabilità, se si aggiungono due condizioni addizionali naturali, esiste una e una sola definizione di probabilità compatibile con le due condizioni. La prima condizione è che p(N(b) − N(a) = k) dipenda soltanto da k e dalla lunghezza b − a. La seconda è la condizione, intuitivamente ragionevole, che la probabilità che due punti appaiano contemporaneamente sia zero.

Daremo una derivazione intuitiva della probabilità risultante. La maggior parte degli sviluppi assiomatici della distribuzione di Poisson equivale a una formulazione precisa di questa idea intuitiva. Ritorniamo per un momento allo spazio campione uniforme su [0,a]; sia E(k, n, a) l'evento per il quale, se nell'intervallo [0, a] si scelgono a caso n punti, esattamente k di questi cadono nell'intervallo [0, x]. È facile verificare nello spazio campione uniforme che

Facciamo ora tendere n e a all'infinito, sotto la condizione che n/a = λ, ove λ rappresenta l'intensità data. È ragionevole supporre che la probabilità limite sia proprio la probabilità dell'evento (N(x) = k) nello spazio campione di Poisson e quindi che

Con un ragionamento analogo si trova

Questo giustifica la nostra scelta della probabilità su Ω, lo spazio campione di Poisson; esso e lo spazio campione del moto browniano sono le due colonne su cui poggia la teoria della probabilità.

3. Variabili casuali

La nozione probabilistica di variabile casuale, che, contrariamente all'opinione un tempo dominante, non è fenomenologicamente identica alla nozione di funzione misurabile, può essere motivata filosoficamente come un approfondimento della nozione matematica ordinaria di ‛variabile'. Nella logica contemporanea una variabile x è un simbolo che può spaziare su un dato insieme e che, quando sia utilizzato in un enunciato, determina un sottoinsieme dell'insieme sul quale gli è consentito variare, per il quale è valido l'enunciato. La nozione probabilistica di variabile casuale deve essere intesa come una generalizzazione di questa nozione. Una variabile casuale è una variabile X, che spazia su un insieme dato, per esempio quello dei numeri reali, ma con la condizione aggiuntiva che siano assegnate delle probabilità con le quali la variabile possa assumere determinati valori. Se i valori assunti da X sono in numero finito, o costituiscono un insieme numerabile {t_n}, la probabilità p_n = p(X = t_n) che X assuma il valore t_n può essere specificata per ciascun t_n dalla condizione che la somma di tutti i p_n sia uguale a 1. Se X varia invece sulla retta reale R, accade sovente che p(X = t) = 0 per tutti i t ∈ R. In questo caso si assegna invece la probabilità p(a ⟨ X ≤ b) che X assuma valori in un determinato intervallo a ⟨ X ≤ b. Questo equivale a specificare una funzione F_X(t) che soddisfi alle condizioni seguenti:

e a porre

p(X ≤ t) = F_X(t).

La funzione F_X(t) si chiama ‛distribuzione di probabilità' della variabile casuale X e, una volta nota F_X(t), p(X ∈ S) può essere calcolata, per ogni insieme misurabile S, mediante l'integrale di Stieltjes

Se la distribuzione di probabilità F_X(t) è una funzione differenziabile, la sua derivata f_X(t) prende il nome di ‛densità di probabilità' della variabile casuale X e chiaramente

Le difficoltà che si presentano quando si considerino contemporaneamente più famiglie di variabili casuali vennero riconosciute già nei primi sviluppi della teoria della probabilità.

Una via d'uscita - lungi per altro dall'essere definitiva - è quella di far ricorso alla teoria della misura. Si riconobbe infatti che, in perfetto accordo con il concetto fenomenologico valido in tutti i casi allora conosciuti, si poteva definire semplicemente una variabile casuale come una funzione reale misurabile su uno spazio campione Ω. La distribuzione di probabilità poteva allora essere definita come la probabilità dell'insieme di tutti gli ω ∈ Ω tali che X(ω) ≤ t, cioè come la probabilità dell'evento (X ≤ t). Per una fortunata coincidenza, la definizione di funzione misurabile implica precisamente che siano misurabili gli eventi (X ≤ t) = {ω ∈ Ω : X(ω) ≤ t). Questa coincidenza condusse i primi probabilisti ad adottare sistematicamente la teoria della misura come base matematica della probabilità, come faremo anche noi d'ora in poi.

Se X₁, ... X_n sono variabili casuali, la loro ‛funzione di distribuzione congiunta' F_{12,,, n}(t₁, ... , t_n) è definita dalla

In modo simile viene definita una successione finita di variabili casuali. Due variabili casuali X e Y sono ‛indipendenti' se

F_XY(t₁ , t₂) = F_X(t₁)F_Y(t₂).

In modo ovvio si introducono le definizioni per insiemi arbitrari di variabili casuali.

Fisicamente si incontrano le distribuzioni di probabilità - per esempio in procedimenti di misurazione - prima di aver introdotto uno spazio campione e prima di aver definito su di esso le variabili casuali; nasce cosi il problema di individuare le proprietà in base alle quali, dato un insieme di funzioni, tali funzioni sono le distribuzioni congiunte di una qualche famiglia di variabili casuali. Questo problema fu risolto da Kolmogorov, con il seguente ‛teorema di consistenza': sia A un insieme, eventualmente non numerabile; si supponga che per ogni sottoinsieme finito {α₁, ... , α_n} di A esista una funzione f_α1 ... _αn (t₁, ..., t_n) soddisfacente alle condizioni analoghe a quelle date in (1); supponiamo inoltre che tutte queste funzioni soddisfino alle seguenti condizioni di consistenza: se {α₁, ..., α_n} è un qualsiasi sottoinsieme finito di A e se π è una permutazione di {1, 2, ... , n}, risulti

se {α₁, ... , α_n} è un qualsiasi sottoinsieme finito di A, per ogni sottoinsieme finito {β₁, ..., β_m} di A contenuto in {α₁ , . . . , α_n}, risulti

Sotto queste condizioni esistono uno spazio campione Ω con σ-algebra di eventi ℰ e probabilità p e una famiglia di variabili casuali {X_α, α ∈ A } definita su Ω, tali che, per tutti i sottoinsiemi finiti {α₁ , . . . , α_n}, si abbia

Una famiglia di variabili casuali si chiama ‛processo stocastico' e lo studio dei processi stocastici serve per mettere a fuoco quelle proprietà che dipendono soltanto dalle distribuzioni congiunte.

L'approfondimento dei concetti del calcolo delle probabilità ha arricchito la teoria della misura indirizzandola verso problemi che a uno specialista di analisi funzionale sarebbero apparsi privi di motivazione. Per esempio, in pura teoria della misura è assai verosimile che nozioni quali quelle di variabili casuali indipendenti e variabili casuali equamente distribuite - variabili casuali cioè che abbiano la stessa distribuzione - sarebbero state ignorate.

A ogni variabile casuale X vengono associati due numeri fondamentali, che sono la ‛media', E(X), e la ‛varianza', Var(X). Se X è una variabile casuale con funzione densità f_X(t), poniamo

In modo simile si procede, per variabili casuali senza una densità, mediante integrali di Stieltjes. Definizioni equivalenti, quando si consideri X come una funzione misurabile su uno spazio campione, sono

La radice quadrata σ = √-V-a-r- (-X-) si chiama ‛deviazione standard' di X. La media misura il valore medio della variabile casuale, mentre la varianza dà una misura del modo in cui i valori si spargono intorno alla media.

Le nozioni di media e di varianza si incontrarono per la prima volta nel campionamento statistico. Un insieme di dati x₁, x₂, ..., x_n, considerato come campione casuale, può essere visto come risultato di misurazioni, soggette a errore, di una grandezza fissata. La media dà la migliore stima del valore effettivo delle misurazioni, mentre la varianza dà un'idea dell'accuratezza del procedimento di misurazione.

La nozione di misurazione iterata della stessa grandezza fisica in condizioni imperfette - per esempio nel caso di misurazioni raccolte da uno strumento fisico o di campionamento statistico di una grandezza quale l'età, l'altezza, o la frequenza con cui una malattia si presenta in una popolazione - ha portato alla scoperta della più importante distribuzione di probabilità: la ‛distribuzione gaussiana' o ‛normale'. Una variabile casuale X ha distribuzione normale con media E(X) = m e varianza Var(X) = E((X − m)²) = σ² quando

Il grafico della densità di una distribuzione normale è la ben nota curva di Gauss o curva a campana.

L'ubiquità di questa distribuzione di probabilità si può attribuire a ragioni disparate. Nel contesto delle misurazioni fu osservato - dapprima in via sperimentale - che un campionamento finito di misurazioni casuali x₁, x₂, ... x_n della stessa proprietà numerica poteva essere utilizzato nel modo migliore per predire ulteriori variazioni della stessa proprietà, considerate come valori casuali della stessa variabile con distribuzione normale, con media, detta ‛media di campionamento',

e varianza, detta ‛varianza di campionamento',

L'analisi statistica relativa a vasti campionamenti si basa ancora largamente su questo semplice fatto, che non ha subito cambiamenti significativi da quando, all'inizio di questo secolo, sir Ronald Fisher creò la statistica moderna. Si può dare una giustificazione matematica di questa ‛inferenza' mediante il teorema del limite centrale o mediante la teoria dell'informazione, ma essa ha certamente un significato filosofico più profondo che appare ancora enigmatico.

Daremo ora alcuni esempi tipici di variabili casuali associate a ciascuno dei quattro spazi campione introdotti precedentemente.

1. Allo spazio campione di Bernoulli viene associata una variabile casuale S_n uguale al numero di successi nei primi n lanci. La densità di probabilità di S_n è la ‛densità binomiale'

Il ‛tempo di attesa' W_n per l'n-esimo successo ha ‛densità binomiale negativa'

2. Se X₁, ..., X_n sono n punti scelti a caso nell'intervallo [0, a], indicheremo con X₍₁₎, X₍₂₎, ... , X_(n) la ‛statistica dell'ordine' e cioè gli stessi punti ordinati in modo crescente. La densità della k-esima statistica dell'ordine è

La densità congiunta di X₍₁₎, ... , X_(n) è la densità normalizzata di Lebesgue nel simplesso 0 ≤ t₁ ≤ t₂ ≤ ... ≤ t_n ≤ a e tutte le altre distribuzioni congiunte possono essere calcolate mediante integrazione. Queste distribuzioni congiunte sono importanti nella statistica non parametrica, quel tipo di statistica, cioè, che si occupa di piccoli campioni sperimentali, caratteristici della biostatistica, quando il teorema del limite centrale e altri metodi adatti per ampi campionamenti si rivelano inefficaci. In questi casi si distribuiscono i campioni in ordine crescente e si confrontano le distribuzioni empiriche delle lacune fra campioni successivi con la distribuzione delle lacune nel caso casuale, cioè la distribuzione delle statistiche dell'ordine; in questo modo si vede, almeno statisticamente, se l'esperimento è significativo.

3. Nella passeggiata aleatoria simmetrica a una dimensione, sia X_n la variabile casuale che dà la posizione di una particella che si muova dall'origine e compia n passi. La distribuzione di probabilità di X_n è

se n + k è pari, e zero negli altri casi. La passeggiata aleatoria si può descrivere meglio dando la distribuzione congiunta delle variabili casuali X_n.

Sia V_2n il tempo dell'ultimo ritorno all'origine nei primi 2n passi. Risulta

È significativo che p(V_2n = 2k) = p(V_2n = 2n − 2k), fatto questo che sembra in contrasto con l'intuizione probabilistica non esercitata. Tali distribuzioni simmetriche si presentano in diversi fenomeni connessi con le passeggiate a caso e con il moto browniano e sono note come leggi dell'arcoseno.

Sia P_n il tempo d'attesa per raggiungere il punto n. Risulta allora

e il tempo d'attesa W_n per l'n-esimo ritorno all'origine ha distribuzione di probabilità

p(W_n = k) = p(P = k − n).

Un'altra variabile casuale con una distribuzione notevole è il numero C_n di volte che la passeggiata aleatoria attraversa - e non tocca soltanto - l'origine nei primi n passi. Si calcola che

p(C_n = 0) ≥ p(C_n = l) ≥ p(C_n =2) ≥ ...

In altre parole, è molto più probabile che nella passeggiata aleatoria non si abbia alcun attraversamento piuttosto che un qualsiasi altro numero di attraversamenti dell'origine.

Una tecnica elegante per stabilire queste e altre proprietà delle passeggiate aleatorie è il seguente principio di riflessione di André. Siano A e B punti interi con B > A ≥ 0. Il numero dei cammini da A e B che ritornano all'origine è uguale al numero di tutti i cammini da − A a B. Una semplice applicazione del principio di riflessione dà il teorema del ballottaggio, secondo il quale, se in una data elezione il candidato A riceve a voti e il candidato B riceve b voti, con a > b, la probabilità che A resti sempre in testa a B, man mano che i voti vengono scrutinati uno per uno, e (a−b)/(a + b).

Per passeggiate aleatorie in dimensione d ≥ 2 uno dei problemi più interessanti e non ancora risolti è quello di determinare la probabilità che, dopo n passi, la passeggiata aleatoria non sia mai ritornata in un posto per il quale era già passata. Per d ≤ 2, la probabilità di ripassare per l'origine è 1 e il previsto tempo di ritorno per d = 2 è ∞. Pólya fu il primo a dimostrare che la probabilità di tornare all'origine per d ≥ 3 è positiva, ma minore di 1.

4. Nello spazio campione di Poisson, sia N(t) il numero di punti che si trovano nell'intervallo [0, t]. La distribuzione congiunta dell'insieme di variabili casuali N(t) o della funzione casuale N(t) si determina come segue: se [t₁, t₂] e [t₃, t₄] sono intervalli disgiunti (e in modo simile si procede per un qualsiasi numero finito di intervalli), le variabili casuali N(t₂) − N(t₁) e N(t₄) − N(t₃) sono indipendenti e hanno la seguente ‛distribuzione di Poisson':

Sia W_n il tempo d'attesa per i'n-esimo punto nel processo di Poisson nell'intervallo [0, ∞). La densità di W_n è la ‛densità gamma'

La distribuzione di W₁, cioè il tempo d'attesa per il primo punto nel processo di Poisson, coincide con la distribuzione esponenziale, la cui densità è

λe^-λt, t ≥ 0.

La distribuzione esponenziale, a sua volta, è l'unica distribuzione ‛senza memoria' sulla retta, l'unica distribuzione, cioè, che soddisfa all'equazione funzionale

P(W₁ > t + s ∣ W₁ > s) = P(W₁ > t).

La funzione N(t) dei processo di Poisson è un semplice esempio di ‛funzione casuale' (una funzione casuale è una famiglia X(t) di variabili casuali indicizzata da un parametro reale t). Un tale processo stocastico descrive l'evoluzione nel tempo di un fenomeno fisico governato da leggi stocastiche di evoluzione, cioè di un fenomeno fisico la cui evoluzione è descritta dal cambiamento nel tempo delle distribuzioni congiunte di probabilità X(t₁), X(t_n). Una classe di funzioni casuali oggetto di intenso studio è quella dei ‛processi con incrementi indipendenti', che possono essere visti come analoghi continui di somme di variabili casuali indipendenti. Essi sono definiti dalla proprietà che le variabili casuali X(t₂) − X(t₁) e X(t₄) − X(t₃) (e in modo simile si procede per qualsiasi numero finito di intervalli) sono indipendenti ogniqualvolta gli intervalli [t₁, t₂] e [t₃, t₄] sono disgiunti. I primi due esempi di processi con incrementi indipendenti sono il processo di Poisson e il moto browniano.

4. Natura del pensiero probabilistico

La sola comprensione della teoria della probabilità non è di grande aiuto per acquistare un'effettiva mentalità probabilistica, che può essere raggiunta soltanto mediante l'applicazione pratica. Daremo qui alcuni esempi allo scopo di mostrare come disparati problemi di matematica possano essere interpretati in modo probabilistico.

a) Geometria integrale

Oltre alla distribuzione di punti dislocati a caso nello spazio, che viene studiata ricorrendo allo spazio campione di Poisson, si possono considerare rette distribuite a caso, o altre figure geometriche disposte a caso nello spazio. Lo studio di configurazioni siffatte è ancora oggi ai suoi inizi; i problemi concettuali più profondi che ancora devono essere risolti - quale, ad esempio, quello della cosiddetta pattern recognition - provengono dalla scienza dei calcolatori. Per esempio, non hanno fatto molti progressi i tentativi di soluzione del problema di identificare e classificare accumulazioni di punti posti a caso o, più in generale, di punti disposti nello spazio secondo le leggi probabilistiche. Questi processi stocastici sono noti come processi puntuali.

Presenteremo qui, a titolo d'esempio, alcuni problemi classici riguardanti le configurazioni casuali di rette nel piano euclideo.

Una retta l in un piano può essere individuata, rispetto a un sistema prefissato di coordinate cartesiane ortogonali, dai parametri ϕ, angolo formato dalla sua normale con l'asse delle x, e p, distanza di l dall'origine. Dunque, se S è un insieme di rette, la sua misura è

ove f(p, ϕ) è una funzione misurabile. Ora, supponendo lo spazio omogeneo, questa misura dev'essere invariante rispetto al gruppo delle isometrie del piano, cioè invariante rispetto alle rotazioni e alle traslazioni. In base a questa restrizione f deve essere una funzione costante. Quindi, a meno di una costante, l'unica misura invariante sull'insieme delle rette è data dalla

dl = dp dϕ.

Sia ora K un insieme limitato e convesso nel piano. Si può dimostrare che la misura dell'insieme H delle rette l che intersecano K è data dall'integrale

ove L è il perimetro di K. Possiamo rienunciare questo risultato probabilistico nel modo seguente: siano K₁ e K₂ due insiemi limitati e convessi; la probabilità che una retta i intersechi K₁, dopo avere intersecato K₂, è L₁/L₂, ove L₁ e L₂ sono i perimetri di K₁ e K₂. Estendendo questo risultato, diventa possibile definire il perimetro di ogni insieme limitato, anche se la sua frontiera non è rettificabile.

Sia ora σ(l) la lunghezza del segmento che l ha in comune con K e sia

Possiamo rienunciare il nostro risultato precedente come segue: I₀ = L. Non è difficile dimostrare che I₁ = πF, ove F è l'area di K. Per calcolare I_n in generale definiamo un'altra misura, questa volta sulle coppie di punti (P₁, P₂). L'unica misura invariante sulle coppie di punti è data dalla

d(P₁ , P₂) = (t₂ − t₁) dp dϕ dt₁ dt₂,

ove ϕ e p sono i parametri della retta l congiungente P₁ e P₂ e t_i è la distanza tra P_i e il piede della perpendicolare abbassata dall'origine a l. Sia

ove r(P₁, P₂) è la distanza tra i punti P₁ e P₂ e l'integrale è esteso a tutte le coppie di punti in K. Gli integrali J_n e I_n sono legati dalla relazione

In base a questa uguaglianza e al fatto che J₀ è - come si vede facilmente - uguale a F², si ottiene

I₃ = 3F².

In generale, per insiemi convessi K, gli integrali J_n sono molto più facili da calcolare che gli I_n. Per esempio, se K è il cerchio di raggio r, si ha

Queste formule integrali si devono a Crofton, che per primo le incluse nell'articolo Probability scritto per la nona edizione della Encyclopaedia Britannica. Il campo della geometria integrale, o probabilità geometrica, venne sviluppato da Blaschke, Chern, Deltheil, Santalò e altri, che si ispirarono a queste e ad altre simili formule di Crofton.

Vogliamo qui indicare un altro tipico problema della probabilità geometrica. Siano K₀ e K₁ insiemi convessi nel piano tali che K₁ ⊂K ₀. Supponiamo che l'insieme convesso K₂, pur essendo dislocato a caso, incontri K₀; allora la probabilità che esso incontri K₁ è

ove f₁ è l'area e g_i è il perimetro di K_i.

b) Teoria non costruttiva dei grafi

Un problema che si presenta frequentemente nella teoria dei grafi è quello di dimostrare l'esistenza di un grafo con una struttura prescritta. Erdös fu il primo a dimostrare che talvolta i metodi probabilistici riescono a dimostrare l'esistenza là dove i metodi costruttivi falliscono. L'esistenza di certi tipi di grafi viene infatti stabilita mostrando che la probabilità della loro esistenza è positiva. Illustreremo questo metodo con un esempio per il quale non è nota nessuna dimostrazione costruttiva.

Un torneo T con n giocatori è un grafo diretto con n vertici (ove ciascun vertice rappresenta un giocatore), tale che, per due qualsiasi vertici x e y, (x, y) è un lato, oppure (y, x) è un lato, non potendo tuttavia essere lati entrambi. Il lato (x, y) deve interpretarsi come ‛x batte y'. Una graduatoria di T è una permutazione σ dell'insieme dei vertici. Consideriamo il seguente criterio per determinare una graduatoria ‛ottima' di T: indichiamo con f(T, σ) il numero dei lati (x, y) in T per i quali σx > σy (la graduatoria cioè è in accordo con il gioco). Una graduatoria ‛ottima' è una graduatoria per la quale f(T, σ) è un massimo. Si osservi che se -σ è la graduatoria inversa di σ, risulta

e pertanto

Siamo ora pronti a dimostrare che, se n è sufficientemente grande, per ogni ε > 0 esiste un torneo per il quale nessuna graduatoria rappresenta 1/2 + ε dei giochi (lati). Sia T un torneo a caso, cioè un torneo in cui la probabilità che (x, y) sia un lato sia 1/2 e tale che, per coppie distinte di lati, le probabilità siano indipendenti. Per un σ fissato, f(T, σ) è una variabile casuale somma di

variabili casuali indipendenti aventi distribuzione di Bernoulli con p = 1/2. Per il teorema del limite centrale, F(x) è approssimativamente una distribuzione normale con speranza

e varianza

Mediante una stima relativa alla distribuzione binomiale, si può dimostrare che, per ogni ε > 0,

onde, per

e quindi, per questa scelta di ε,

per ogni σ particolare e per un n sufficientemente grande. Di conseguenza

Abbiamo così dimostrato che esiste un torneo T per il quale

c) Zeri di polinomi casuali

Un polinomio casuale (nella variabile z) è un polinomio della forma

P(z) = a_nzⁿ + a_n-1z^n-1 + ... + a₁z + a₀,

ove i coefficienti a_k sono variabili casuali e a_n ≠ 0 con probabilità 1. I polinomi casuali si presentano in svariate circostanze, per esempio nella teoria spettrale delle matrici con elementi casuali.

Il ‛numero delle radici' è una variabile casuale la cui distribuzione è stata ampiamente studiata soprattutto per quanto riguarda il numero delle radici reali e la loro media ν(R), sotto la condizione che i coefficienti a_k siano variabili casuali indipendenti equidistribuite. Per esempio, Bloch e Pólya hanno considerato i polinomi casuali a valori reali di grado n

P_n(x) = xⁿ + a_n-1c^n-1 + ... + a₁x + a₀,

sotto l'ipotesi che, per ogni 0 ≤ k ≤ n − 1,

Essi hanno mostrato che

ξ_n(R) = O(√-n) per n → ∞.

M. Kac ha considerato la classe dei polinomi reali casuali i cui coefficienti sono variabili casuali indipendenti con distribuzione normale con media 0 e deviazione standard 1, dimostrando che

ove

e deducendone il risultato asintotico

ν_n(R) ~ (2/π) log n, n → ∞.

Considerando la media del numero di radici in un dato intervallo, Kac mostrò che le radici reali, in media, sono concentrate intorno a x = ± 1.

Dunnage ha considerato variabili casuali arbitrarie indipendenti a valori complessi le cui distribuzioni di probabilità ammettono funzioni densità. Per questa classe di polinomi casuali egli ha dimostrato il risultato sorprendente secondo cui la probabilità che P(z) abbia radici multiple in qualche parte del piano complesso è zero.

d) Teoria dei numeri probabilistica

Ci si aspetta, intuitivamente, che, dati due numeri primi distinti a e b, le due possibilità che un intero a caso sia divisibile per a oppure per b costituiscano eventi indipendenti. Le probabilità naturali sugli interi che ciò sia vero sono definite mediante la funzione zeta di Riemann ζ(s):

Sotto opportune condizioni sull'insieme A, il limite P₈(A), quando il parametro reale s tende a 1decrescendo, è la ‛densità aritmetica' (che non è una probabilità numerabilmente additiva)

Molti risultati della teoria dei numeri possono essere dimostrati mediante metodi probabilistici usando questi spazi campione. È molto notevole che Fuchs sia riuscito a dare, lungo queste linee, una dimostrazione probabilistica del teorema di Dirichlet sui numeri primi in una progressione aritmetica.

e) Distribuzione delle prime cifre

Chiunque abbia avuto occasione di consultare una vecchia tavola numerica, per esempio una tavola di logaritmi, avrà senz'altro notato che tali manuali sembrano maggiormente logorati all'inizio, ossia nelle pagine che corrispondono alle cifre più basse, che alla fine, cioè nelle pagine corrispondenti alle cifre più alte. Rilevamenti statistici hanno dimostrato senza ombra di dubbio che la distribuzione delle prime cifre significative in queste tavole è una variabile casuale X che assume valori 1, 2,..., 9 tali che p(X = k) = log(k + 1) − log k. Sono state avanzate molte spiegazioni di questo fenomeno, ma fino a ora nessuna sembra veramente convincente.

f) Accrescimento delle cellule

Un ‛organismo' può essere definito, in modo estremamente semplificato, come un insieme connesso di quadrati unitari nel piano (i quali si toccano lungo i lati e non solo nei vertici). A ogni unità di tempo un quadrato, o ‛cella', viene aggiunto in una posizione casuale sulla frontiera dell'organismo, sotto la condizione che l'organismo risultante sia ancora connesso. Le leggi stocastiche di accrescimento di tale struttura rimangono largamente sconosciute e una chiarificazione di questo fenomeno condurrebbe probabilmente a una nuova e interessante classe di processi stocastici.

g) Monete su un tappeto

La costruzione del procedimento di Poisson può essere generalizzata in modo da definire dei punti a caso su una qualsiasi superficie liscia sulla quale sia definita una misura. Basta semplicemente assegnare probabilità

all'evento consistente nel fatto che n punti ‛appaiano' su una superficie di area uguale ad a, con la condizione che i punti che appaiono in aree disgiunte siano eventi indipendenti. In dimensione maggiore di 1 anche i problemi più semplici relativi a queste configurazioni sono ancora aperti. Per esempio, qual è la distribuzione di probabilità della distanza minima di n punti posti a caso ‛alla Poisson' nel piano? In termini concreti, se si lasciano cadere a caso n monete su un tappeto, qual è la probabilità che nessuna coppia di esse si sovrapponga almeno parzialmente? La soluzione di questo problema avrebbe applicazioni significative nella meccanica statistica.

5. Somme di variabili casuali indipendenti

Due variabili casuali X e Y sono indipendenti quando per tutti gli a e b

p((X ≤ a) ⋂ (Y ≤ b)) = p(X ≤ a)p(Y ≤ b);

in altre parole, quando ogni evento che sia definibile mediante X è indipendente da ogni evento che possa essere definito mediante Y. Questa definizione può essere estesa a un numero arbitrario di variabili casuali.

Una nozione più raffinata è l'interscambiabilità delle variabili casuali. Diremo che un insieme (eventualmente infinito) di variabili casuali X₁, X₂, ... è ‛interscambiabile' quando la loro distribuzione congiunta è invariante rispetto a ogni permutazione degli indici di tutti i sottoinsiemi finiti. Variabili casuali indipendenti sono interscambiabili. Tuttavia, se mettiamo k biglie in n scatole, il numero di biglie in ogni scatola è un insieme di variabili casuali che è interscambiabile, ma non indipendente.

Due variabili casuali si dicono equidistribuite, o ugualmente distribuite, se hanno la stessa distribuzione di probabilità. I procedimenti stocastici maggiormente studiati sono successioni di variabili casuali indipendenti equidistribuite; il che, grosso modo, è l'equivalente probabilistico del concetto di iterazione dello stesso esperimento casuale.

Poiché le variabili casuali possono essere considerate come funzioni misurabili su uno spazio campione, i vari tipi di convergenza considerati in analisi funzionale danno nozioni corrispondenti di convergenza per successioni di variabili casuali. Per esempio la convergenza quasi ovunque diventa convergenza con probabilità 1 e la convergenza in misura diventa la convergenza in probabilità. Esiste tuttavia una nozione di convergenza che appartiene essenzialmente alla teoria della probabilità: la convergenza in distribuzione.

Si dice che una successione di variabili casuali converge in distribuzione, o ‛in legge', a una variabile casuale X, quando la distribuzione di probabilità F_n(x) di X_n (ma non necessariamente la densità) converge alla distribuzione F(x) di X in ogni punto di continuità di F(x). La successione X_n può convergere in distribuzione a X anche se non vi è nessun punto ω nello spazio campione Ω in cui la successione di numeri X_n(ω) converga a X(ω).

Si può intuire la forza di queste nozioni di convergenza quando si prendono in considerazione quattro classici teoremi di limite per somme di variabili casuali indipendenti. Sia X_n una successione di variabili casuali, indipendenti, equidistribuite, di media m e di varianza finita σ². Ciascuno di questi teoremi di limite corrisponde esattamente alla previsione intuitiva che la media

si avvicini alla media m, per n sufficientemente grande. Questa intuizione sta alla base della nozione attuale di probabilità.

La ‛legge debole dei grandi numeri' afferma che per tutti gli ε > 0.

quando n → ∞. La ‛legge forte dei grandi numeri' afferma che

La ‛legge del logaritmo iterato' afferma che, con probabilità 1,

Il ‛teorema del limite centrale', che è il più forte dei quattro, afferma che per tutti gli a e b e per n → ∞

Ciascuno di questi risultati è stato ampiamente generalizzato a successioni più generali di variabili casuali.

Daremo una semplice applicazione del ‛teorema del limite centrale'. Due aviolinee concorrenti hanno un volo da New York a Los Angeles che parte alla stessa ora e ha lo stesso numero, s, di posti. Se n passeggeri scelgono una delle due aviolinee indipendentemente e a caso, il risultato è quello di n esperimenti di Bernoulli indipendenti, con p = 1/2. Se il numero s dei posti è minore di n, la probabilità p(s) che alcuni passeggeri non siano accettati da un volo è positiva e può essere approssimata dal teorema del limite centrale

Se le due aviolinee decidono di accettare un livello di rischio r tale che p(s) > r, basta che sia

ove z soddisfa

e si può trovare nelle tavole. Per fare un esempio numerico, se n = 1000 e r = 0,01 è z ≃ 2,33 e basteranno 537 posti; allo stesso modo 549 posti saranno sufficienti in 999 casi su 1.000.

Famiglie di variabili casuali, o procedimenti stocastici, vengono classificate mediante le loro distribuzioni congiunte e molto lavoro è stato necessario per individuare quei processi stocastici che si presentano nei più svariati casi concreti, quali ad esempio, la distribuzione di ammassi di stelle, le fluttuazioni del mercato azionario, o i rumon casuali nei segnali delle telecomunicazioni.

Malgrado la generalità del concetto di processo stocastico, si è rilevato che assai pochi tra i processi stocastici che si sono dimostrati rilevanti richiedono necessariamente il concetto di variabile casuale indipendente. Forse per questa ragione K.L. Chung definisce la probabilità come lo studio dell'indipendenza stocastica e delle perturbazioni di questa nozione.

Un notevole sforzo è stato compiuto per la classificazione di quelle variabili casuali le cui distribuzioni si riproducono quando si sommi ripetutamente. Più precisamente, si dice che una distribuzione di probabilità F(x) è ‛stabile' se, ogniqualvolta X₁, X₂, ... , X_n sono variabili casuali indipendenti, equidistribuite con distribuzione F(x), la variabile casuale X₁ + . . . + X_n ha la stessa distribuzione di c_nX + b_n, ove X è una variabile casuale con distribuzione F(x). Pertanto la variabile casuale X₁ + . . . + X_n ha distribuzione uguale a F(x) eccetto per un cambio di scala e di origine.

La ricerca di distribuzioni stabili di variabili casuali reali ha rappresentato uno dei problemi più importanti nella prima metà di questo secolo, la cui completa risoluzione è dovuta a P. Lévy. Uno dei fatti fondamentali della probabilità è che l'unica distribuzione continua, stabile, di varianza finita è la distribuzione normale. Più in generale, le distribuzioni stabili e continue (non concentrate in un punto) possono essere caratterizzate dal fatto che c_n = n^1/x, per 0 > α ≤ 2. La costante α prende il nome di ‛esponente caratteristico' della distribuzione stabile. Per α = 2 si ottiene la distribuzione normale. Si può prevedere che, nel futuro, le distribuzioni stabili verranno identificate con i procedimenti stocastici che si verificano in natura, allo stesso modo in cui la distribuzione normale viene associata al moto browniano.

Una tecnica efficace per ottenere la classificazione delle distribuzioni stabili è l'analisi armonica. Si associa a una variabile casuale X la sua funzione caratteristica ϕ_X(u), definita dalla

ove f(t) è la densità e F(t) la distribuzione della variabile casuale X.

La funzione caratteristica determina univocamente la distribuzione della variabile casuale. La densità della somma di due variabili indipendenti X e Y è la convoluzione

e quindi la funzione caratteristica della somma X + Y è il prodotto delle funzioni caratteristiche individuali. L'algebra delle distribuzioni di probabilità viene pertanto semplificata passando alle trasformate di Fourier. L'utilità del metodo delle funzioni caratteristiche diventa particolarmente evidente quando si prenda in considerazione la convergenza in distribuzione.

Mediante il metodo delle funzioni caratteristiche, alcune delle leggi limite di cui abbiamo precedentemente parlato sono state generalizzate a variabili casuali con medie e varianze diverse e addirittura a variabili casuali non indipendenti. La funzione caratteristica è stata altresì utilizzata per formulare le leggi stabili generali. Sia X una variabile casuale con distribuzione stabile e funzione caratteristica ϕ_X(u). In tal caso, o X ha una distribuzione normale, oppure esiste un numero α, 0 ⟨ α ⟨ 2, l'esponente caratteristico, e due costanti reali, m₁ > 0, m₂ > 0, tali che

Una variabile casuale X ha una distribuzione ‛infinitamente divisibile' se, per ogni intero positivo n, esistono n variabili casuali indipendenti e identicamente distribuite X1⁽ⁿ⁾, ..., Xn⁽ⁿ⁾ tali che X sia equidistribuita con X1⁽ⁿ⁾ + X2⁽ⁿ⁾ + ... + Xn⁽ⁿ⁾. Per esempio, la distribuzione di Poisson e la distribuzione normale sono infinitamente divisibili. P. Lévy scopri che tutte le distribuzioni infinitamente divisibili possono essere ‛sintetizzate' dalle distribuzioni normali e da quelle di Poisson. Il significato di questo termine può essere spiegato nel modo migliore utilizzando le funzioni caratteristiche. La funzione caratteristica ϕ(u) di una distribuzione infinitamente divisibile ha la forma

ove μ è una misura finita tale che μ ({0}) = 0.

La funzione caratteristica ϕ(u) della distribuzione di Poisson è

ϕ(u) = e^λ(eiu-1)

e la funzione caratteristica della distribuzione normale (di media 0) è

ϕ(u) = e^σ2u2/2;

si vede così che la distribuzione generale infinitamente divisibile è una ‛sovrapposizione' di queste due.

6. Probabilità condizionata

La funzione di distribuzione di probabilità è soltanto una delle due strutture mediante le quali si studiano le variabili casuali. La definizione della seconda struttura di questo tipo richiede l'uso sistematico della teoria della misura. Se X è una variabile casuale su uno spazio campione Ω con σ-algebra di eventi Ε e probabilità p, seguendo Rényi, definiremo l'‛informazione Ε (X) fornita dalla variabile casuale X' come la più piccola σ-sottoalgebra di ℰ rispetto alla quale X è una funzione misurabile. Nel caso più semplice, X assume soltanto valori interi e ℰ(X) è la σ-algebra atomica generata dagli eventi (X = n). La σ-sottoalgebra ℰ(X) esprime la quantità di informazione contenuta nella variabile casuale X; quanto più grande, o più ‛fine', è ℰ(X), tanto più la conoscenza dei valori di X ci permette di distinguere i punti nello spazio campione Ω.

Data una successione X₁, X₂, ... di variabili casuali, l'‛informazione congiunta' di {_nl}, in simboli ℰ (X₁, X₂, ...), è la più piccola σ-algebra - o ‛unione' nel senso della teoria dei reticoli - di tutte le σ-algebre ℰ (X_i). Equivalentemente ℰ (X₁, X₂, ...) è la più piccola σ-algebra rispetto alla quale tutte le variabili casuali {X_i} sono misurabili. Se {X_n} sono variabili casuali indipendenti, diremo che le σ-algebre di informazione {ℰ(X_n)} sono ‛indipendenti'. Definizioni analoghe valgono per ogni famiglia di variabili casuali.

Un'applicazione elementare estremamente interessante del concetto di a-algebra di informazione è la ‛legge zero-uno' di Kolmogorov. L'‛intersezione' di qualsiasi numero di σ-algebre {ℰ_α} è la famiglia di tutti gli eventi E tali che E sia un elemento di ℰ_α, per tutti gli α; l'intersezione è, a sua volta, una σ-algebra. Data una successione di variabili casuali {X_k}, un ‛evento di coda' è, per definizione, un qualsiasi evento indipendente dalle prime n variabili X₁, X₂, , X_n per ogni n. Più precisamente, posto ℰ_n = ℰ(X_n+1 X_n+2, ...), un evento di coda E si presenta in ogni ℰ_n o, meglio, E è un elemento dell'intersezione delle σ-algebre ℰ_n. La legge di Kolmogorov stabilisce che, se le variabili casuali X_k sono indipendenti, ogni evento di coda ha probabilità 0 oppure 1. Per esempio, consideriamo una serie infinita Σ n^∞₌₀ a_nX_n per una data successione di numeri reali a_n. Una serie siffatta converge con probabilità O oppure 1, poiché l'evento rappresentato dalla convergenza della serie è un evento di coda. Quest'idea è stata alla base di molte ricerche sulle serie di Fourier e sulle serie di potenze con coefficienti casuali. Il risultato più antico, e al tempo stesso più classico, è il teorema di Rademacher secondo il quale la serie Σ n^∞₌₀ ± a_n, ove i ‛+' e i ‛−' sono distribuiti a caso, converge con probabilità uguale a 1 o a O a seconda che Σ n^∞₌₀ a_n sia finita oppure no. In proposito, con una tecnica più raffinata, si ha il seguente teorema di Kolmogorov sulle tre serie.

Se X è una variabile casuale, dato s > 0, la ‛troncatura' di X in s, che indicheremo con X^(s), è definita dalla

Sia X₁, X₂, . . . , X_n, una successione di variabili casuali indipendenti. Se per ogni s > 0

la serie ΣX_k converge con probabilità 1, altrimenti converge con probabilità 0.

Allo scopo di quantificare l'informazione contenuta nella variabile casuale X, Rényi, Shannon, Wiener e altri hanno cercato di assegnare valori numerici alle σ-sottoalgebre ℰ(X). Questi tentativi hanno avuto solo parzialmente successo, soprattutto perché la struttura combinatoria del reticolo delle σ-sottoalgebre di ℰ non è mai stata adeguatamente esaminata. Se Ω è un insieme finito, questo reticolo è isomorfo al reticolo delle partizioni di Ω; pertanto il reticolo delle σ-sottoalgebre di ℰ può essere visto come un analogo infinito del reticolo delle partizioni. Questo reticolo sembra poter sostenere un ruolo complementare a quello del reticolo - o σ-algebra di Boole - degli eventi. È questo un campo di ricerche che deve essere ulteriormente approfondito. Il valore numerico naturale associato a un evento è la sua probabilità; analogamente, il valore numerico naturale associato a una σ-sottoalgebra di informazione ℰ(X) è l'‛entropia' di Shannon-Wiener H(ℰ(X)). Definiamo anzitutto H quando la σ-algebra ℰ(X) è generata da un insieme numerabile di ‛atomi' {n}. In questo caso poniamo

H(ℰ(X)) = − Σ p(n) log₂p(n).

L'entropia è additiva sulle σ-algebre indipendenti e in generale si ha

L'entropia è una misura di incertezza, come si desume chiaramente dal semplice esempio che segue. Se ci viene proposto di indovinare un intero tra 1 e 2ⁿ, ci interesserebbe determinare il numero minimo di tentativi necessari ad assicurarci di avere indovinato. Il nostro spazio campione Ω consta degli interi fra 1 e 2ⁿ nella loro rappresentazione binaria e noi consideriamo la famiglia di variabili casuali indipendenti {X_i}, ove X_i(ω) assume il valore 0 o 1 a seconda che sia 0 o 1 la i-esima cifra del dato ω ∈ Ω. Un semplice calcolo mostra che

così che, come era prevedibile, il numero minimo di tentativi è n.

Un'immagine intuitiva della nozione di entropia si può ricavare dall'esempio seguente, dovuto a Shannon, il quale ci introduce nella vasta area della teoria dell'informazione. Un ‛linguaggio' è una successione doppiamente infinita di variabili casuali , X_-2, X_-1, X₀, X₁, X₂, . . , in generale non indipendenti ma con probabilità congiunte stazionane, con valori in un alfabeto A costituito da un numero finito di lettere, per fissare le idee 1, 2,..., n. Si dimostra che esiste il limite

ove la sommatoria è estesa a tutte le successioni i₁, i₂, ..., i_n in A. Questo limite misura la ridondanza del linguaggio. Un linguaggio con entropia H può essere codificato nel linguaggio costituito dalle variabili indipendenti X_i che prendono valore 0 e 1, in guisa tale che una lettera richieda, in media, una successione con un numero H di valori 0 e di valori 1 per una codificazione fedele.

Un grande sforzo è stato compiuto per estendere la definizione di entropia alle σ-algebre non generate da atomi. Procedimenti di limite sono stati utilizzati essenzialmente dalla scuola russa. E stata anche proposta una definizione di entropia mediante X piuttosto che ℰ (X). Se X ha una funzione di densità continua f(t), si ponga

Un vantaggio di questa definizione è che, fra tutte le distribuzioni aventi densità continua e varianza uguale a 1, la distribuzione normale ha entropia massima. Ciò offre una spiegazione suggestiva del fatto intuitivo che la distribuzione normale rappresenta il disordine massimo e giustifica anche la priorità che viene data ai metodi statistici quando non si abbia un'adeguata quantità di informazione.

Un'ulteriore utilizzazione della σ-algebra d'informazione ℰ(X) di una variabile casuale X si presenta quando si considerino le probabilità condizionate e le medie condizionate. La ‛media condizionata' di una variabile casuale X relativa a una variabile casuale Y, in simboli E(X ∣ ℰ (Y)) o E(X ∣ Y), è una variabile casuale z, che è ℰ (Y)-misurabile e gode della proprietà seguente:

E(I_A Z) = E(I_AX)

per tutti gli eventi A ∈ ℰ (Y), ove I_A è l'indicatore di A, cioè I_A è la funzione

In particolare, se X e Y sono variabili casuali indipendenti, si ha E(X ∣ Y) = E(X). Utilizzando il teorema di Radon-Nikodym, si può dimostrare che la media condizionata esiste sempre. La media condizionata è probabilmente l'idea più sofisticata della teoria della probabilità e è essenziale nella definizione dei processi stocastici. La si può meglio comprendere esaminando la sua versione più elementare, vale a dire la probabilità condizionata. Sia Z = E(I_A ∣ I_B). Per definizione la variabile casuale Z assume due valori, in quanto la σ-algebra ℰ (I_B) è generata dai due atomi B e B^C:

Pertanto la probabilità condizionata è il caso più semplice di media condizionata. La regola delle probabilità composte è uno degli strumenti più utili della probabilità. Secondo questa regola

ove {A_n} è una partizione dello spazio campione e il suo analogo continuo è

ove f_X(t) è la densità di X e p(B ∣ X = t), per quanto intuitivamente chiaro, richiede una definizione elaborata.

Illustreremo questi concetti facendo ricorso a un sorprendente risultato di De Finetti, secondo il quale ogni successione infinita X₁, X₂, ... di variabili casuali intercambiabili, che per semplicità supporremo assumano i valori 0 e 1, può essere considerata come il risultato della casualizzazione del parametro p, cioè come una successione di variabili casuali ‛indipendenti' le quali assumano i valori 0 con probabilità p e 1 con probabilità 1 -p, p essendo a sua volta una variabile casuale. Se f(t) è la densità della variabile casuale p, la regola precedente delle probabilità composte dà, per l'evento

A = (X₁ = 1) ⋂ (X₂ = 1) ⋂ ... ⋂ (X_k = 1) ⋂

⋂ (X_k+1 = 0) ⋂ ... ⋂ (X_n = 0),

la sua probabilità, p(A), mediante la formula:

che è la versione analitica del risultato di De Finetti.

7. Teoria ergodica e martingale

Per quanto la definizione ormai comunemente accettata di processo stocastico (come famiglia di variabili casuali) ammetta in linea di principio infinite possibilità, di fatto soltanto poche classi di processi stocastici si sono dimostrate accessibili alla ricerca: martingale, processi di Markov, processi stazionari e loro varianti. Negli ultimi trent'anni non è stato, di fatto, scoperto nessun processo stocastico veramente nuovo e trattabile e il ricorso sistematico alle vecchie idee ha dato luogo a un'atmosfera di crisi.

Un ‛processo stazionario' è una successione doppiamente infinita di variabili casuali ... , X_-2, X_-1, X₀, X₁, X₂, ..., tale che la distribuzione congiunta di ogni sua sottosuccessione finita sia invariante rispetto alla traslazione degli indici. Lo spazio campione Ω (v. lo spazio campione per le passeggiate aleatorie) si costruisce prendendo tutte le successioni doppiamente infinite (x_i) di numeri reali. Gli eventi

{a₁ ≤ x_i ≤ b₁, ..., a_n ≤ x_i+n ≤ b_n},

le cui probabilità sono date dalla distribuzione congiunta delle variabili casuali X_i, ... X_i+n, generano la σ-algebra degli eventi su Ω. Poiché il processo è stazionario, la trasformazione T che manda (x_n) in (x_n+1) è una trasformazione di Ω che conserva la probabilità (o, come si usa dire più spesso, conserva la misura); cioè, per ogni evento E ⊆ Ω, T(E) e T^-1(E) sono anch'essi eventi e

p(T^-1(E)) = p(E) = p(T(E)).

La ‛teoria ergodica', cioè lo studio delle trasformazioni che conservano la misura su spazi di misura e specialmente su spazi di probabilità, è motivata soprattutto da questa connessione con i processi stazionari.

La teoria ergodica è diventata una teoria indipendente e ricca di risultati che si occupa della classificazione delle trasformazioni che conservano la misura a meno di un coniugio. Si dice che una trasformazione che conserva la misura T è ‛coniugata' alla trasformazione che conserva la misura T′, se esiste un automorfismo α che conserva la misura, tale che

T = αΤ′α^-1.

La definizione si può facilmente estendere a trasformazioni che conservano la misura su spazi di probabilità o di misura distinti. La classificazione delle trasformazioni che conservano la misura è un problema ancora aperto ed estremamente affascinante. Disponiamo oggi di due risultati importanti in questa direzione; ambedue hanno condotto a numerose generalizzazioni.

Osserviamo che basta considerare trasformazioni ‛ergodiche', cioè trasformazioni T tali che T(E) = T^-1(E) = E (a meno di un insieme di misura zero) implichi p(E) = 0 o p(Ω/E) = 0. Ogni trasformazione che conserva la misura si decompone in un integrale diretto di trasformazioni ergodiche che conservano la misura.

Il primo risultato è una classificazione completa delle trasformazioni ergodiche con spettro discreto. Una trasformazione ergodica T sullo spazio di misura Ω induce un operatore unitario U_T su L²(Ω), lo spazio di Hilbert delle variabili casuali a valori complessi e a quadrato integrabile, dato dalla

U_T(f) = f ???15???T

per f ∈ L²(Ω). Diremo che la trasformazione T ha ‛spettro discreto' se U_T ha spettro discreto. Una trasformazione ergodica con spettro discreto è coniugata a una rotazione su un gruppo compatto abeliano. Inoltre due trasformazioni ergodiche con spettri discreti sono coniugate se, e soltanto se, gli operatori unitari indotti da esse sono unitariamente simili (come operatori su uno spazio di Hilbert).

Il secondo risultato è la classificazione, dovuta a Ornstein, delle traslazioni (shifts) di Bernoulli. Consideriamo lo spazio di probabilità Ω = ΠA_n al variare di n sugli interi e supponiamo che ciascun A_n sia uno spazio finito di probabilità, costituito da k punti a₁, ... , a_k, e che la probabilità del punto a_i sia p_i. Una ‛traslazione di Bernoulli' T è la trasformazione che conserva la misura su Ω definita dalla

T(x_n) = (x_n+1),

ove

x_n ∈ A_n, (x_n) ∈ Ω.

L'‛entropia' della traslazione di Bernoulli T è definita dalla

Il teorema del coniugio di Ornstein afferma che due traslazioni di Bernoulli T e T′ sugli spazi Ω e Ω′ sono coniugate se, e soltanto se, hanno la stessa entropia.

Stoncamente il primo risultato ottenuto nella teoria ergodica è il teorema di ricorrenza di Poincaré; sia T una trasformazione non ergodica di uno spazio di probabilità non atomico; allora se A ⊆ Ω è un evento con probabilità positiva, esiste un intero n tale che

p(Tⁿ(A) ⋂ A) > 0.

Questo risultato, che si dimostra facilmente, è stato ulteriormente migliorato; ci limiteremo a ricordare, in proposito, una formula di Kac. Data una trasformazione ergodica T e un evento A con probabilità positiva, definiamo la variabile casuale n_A(ω) come il più piccolo intero positivo n tale che Tⁿ(ω) ∈ A se ω ∈ A. Il teorema di ricorrenza di Poincaré afferma che n_A è finito con probabilità 1; secondo la formula di Kac, il valore medio della variabile casuale I_An_A è 1, essendo I_A l'indicatore dell'evento A.

Indicheremo schematicamente la dimostrazione di questo risultato che utilizza lo stacking method (metodo dell'accatastamento), una delle tecniche fondamentali nello studio delle trasformazioni che conservano la misura.

Sia A_n l'evento per il quale n_A = n. Risulta A_n ⊆ A e gli insiemi A_n, T(A_n), T²(A_n), . . . , T^n-1(A_n) sono disgiunti e hanno la stessa probabilità. Per il teorema di ricorrenza di Poincaré, l'unione degli A_n, per n = 1, 2, ..., coincide con A a eccezione che per un evento di probabilità zero. Quindi

Ma la trasformazione T è ergodica e, poiché l'evento

è invariante rispetto a T, esso deve coincidere, ad eccezione che per un evento di probabilità zero, con l'intero spazio campione Ω. Di conseguenza il secondo membro della (2) è uguale a 1. Più esplicitamente, il risultato di Kac afferma che, in media, il ‛tempo di ricorrenza' per un punto campione di A è 1/p(A).

L'applicazione forse più suggestiva della nozione di ricorrenza è la dimostrazione, recentemente effettuata da Furstenberg, del seguente risultato di Szemerédi. Sia B un insieme di interi positivi con densità aritmetica superiore positiva, cioè

In questa ipotesi B contiene progressioni aritmetiche arbitrariamente lunghe.

I teoremi di limite della teoria della probabilità (particolarmente la legge forte dei grandi numeri) trovano la loro generalizzazione finale nella teoria ergodica. Nel suo enunciato classico, il teorema ergodico di G. D. Birkhoff afferma che, per ogni trasformazione T che conserva la misura su uno spazio di probabilità Ω e per ogni variabile casuale f in L¹(Ω), le medie ergodiche

convergono con probabilità 1. Se T è ergodica, il limite è ∫_Ωf dp. Esistono diverse generalizzazioni di questo teorema, ma le più avanzate sono quelle di Chacón e Ornstein e di A. Garsia.

Per poter applicare il teorema ergodico, e anche per altre ragioni, è importante sapere se una trasformazione misurabile ha una misura di probabilità invariante equivalente. Se S è una trasformazione misurabile su Ω, ciò implica, in particolare, che per ogni evento A anche S(A) e S^-1(A) sono eventi. Si dice che la trasformazione misurabile S è ‛non singolare' (rispetto alla misura p) se, per ogni evento A di misura zero, S^-1(A) e S(A) sono ambedue di misura zero. Una misura p su Ω si dice ‛invariante per una trasforzione misurabile S' quando p(S(A)) = p(A) per ogni evento A. Si ricordi che due misure μ e ν sono ‛equivalenti' quando hanno gli stessi insiemi nulli: cioè μ(A) = 0 se, e soltanto se, ν(Α) = 0. Il risultato definitivo è il seguente teorema di Hajian e Kakutani: sia S una trasformazione misurabile su uno spazio di misura Ω che sia σ-finito rispetto a una misura μ. Esiste allora una misura di probabilità p invariante rispetto a S ed equivalente a μ se, e soltanto se, S non ha insiemi debolmente vaganti. Un ‛insieme debolmente vagante' per la trasformazione S è un insieme misurabile A per il quale esiste una successione strettamente crescente di interi positivi n_i tale che gli insiemi Sⁿⁱ(A) siano disgiunti due a due.

Consideriamo un esempio di trasformazione che conserva la misura tipico della teoria delle frazioni continue. Ricordiamo che un numero reale x, 0 ⟨ x ≤ 1, può essere sviluppato in frazione continua

La successione di interi positivi {a_i} è data dalla formula

a_i(x) = a(T^i-1x),

in cui a e T sono le seguenti funzioni:

dove [x] è la parte intera di x, ossia il più grande intero minore o uguale a x.

Le a_i possono così essere considerate come le funzioni su [0,1] che sono le iterate di una trasformazione T sullo spazio di misura Ω = (0,1] e cioè a_i = UT^i-1a.

La trasformazione T ha una misura di probabilità invariante data dalla

per ogni insieme di Borel A. Risulta che T è di fatto ergodica e, per il teorema ergodico di Birkhoff (per la funzione f(x) = log[l/x)), si ha

con probabilità 1. Passando agli esponenziali, otteniamo (ancora con probabilità 1)

ove c è la costante (indipendente da x)

Questo teorema, del quale era stata data una complicata dimostrazione diretta da Khintchine, è stato ottenuto da Ryll-Nardzewski come semplice applicazione del teorema ergodico.

La classificazione rispetto al coniugio delle trasformazioni che conservano la misura è un problema che ricorda la classificazione degli operatori unitari - o, più in generale, degli operatori limitati in uno spazio di Hilbert - rispetto alla similitudine; questa analogia ha suggerito diverse congetture e concetti nell'ambito della teoria ergodica. Per esempio, un analogo probabilistico della nozione di sottospazio chiuso di uno spazio di Hilbert è la nozione di σ-sottoalgebra di ℰ e il problema di trovare sottospazi chiusi invarianti di operatori lineari suggerisce il problema analogo posto per la prima volta da Halmos: data una qualsiasi trasformazione che conserva la misura su uno spazio di probabilità, esiste una σ-sottoalgebra invariante?

Seguendo questa analogia, la nozione di risoluzione spettrale per operatori unitari - una famiglia crescente di sottospazi chiusi di uno spazio di Hilbert - suggerisce la nozione di ‛successione stocastica' - un insieme linearmente ordinato di σ-sottoalgebre ℰ_t, parametrizzato dalla retta reale o dagli interi, tale che ℰ_t ⊆ ℰ_s, quando i ≤ s.

Da questo concetto prende l'avvio la ‛teoria della predizione'. A ogni processo stocastico X_n indicizzato, per semplicità, dagli interi, si associa una successione stocastica ℰ_n come σ-sottoalgebra di informazione congiunta delle variabili casuali X_i con i ≤ n. Questa successione stocastica formalizza la nozione di informazione fornita dal passato fino al tempo n. La media condizionata E(X_n+1 ∣ ℰ_n) misura la possibilità di predire X_n+1 conoscendo il passato. Sono state compiute molte ricerche per sviluppare forme esplicite per questa media condizionata (in particolare da Dym, Kolmogorov, Masani, McKean, Wiener), soprattutto per il caso dei processi gaussiani.

Un altro concetto associato a quello di processo stocastico è quello di ‛martingala'. Una successione X_n di variabili casuali (prendendo ancora per semplicità il parametro in un insieme discreto) si chiama ‛martingala' ogniqualvolta la σ-sottoalgebra di informazione di X_n contiene la σ-sottoalgebra di informazione di X_n-1 e la media condizionata di X_n+1 data da ℰ(X_n), è X_n. La teoria delle martingale è stata sviluppata in larga misura da Doob. Il risultato più rilevante è il ‛teorema di convergenza delle martingale': se {X_n} è una martingala e

esiste con probabilità uno e E ∣ X ∣ > ∞.

Come esempio di applicazione delle martingale tratteggiamo una dimostrazione del seguente risultato classico. Sia u(x) una funzione reale definita su tutti i punti x = (m, n) con coordinate intere nel piano, la quale sia armonica in senso discreto, cioè

u(x) = [u(x₁) + u(x₂) + u(x₃) + u(x₄)]/4,

ove gli x_i (i = 1, 2, 3, 4) sono i quattro punti più vicini al punto x. Supponiamo inoltre che u sia limitata sul piano; in questa ipotesi u è costante.

L'idea su cui si fonda la dimostrazione probabilistica è la seguente. Sia Y_n la posizione al tempo n di una passeggiata aleatoria simmetrica sui punti interi del piano, che abbia inizio, per fissare le idee, nell'origine. Si verifica che X_n = u(Y_n) è una martingala limitata e quindi, per il teorema di convergenza delle martingale, converge con probabilità 1 a una variabile casuale Z. Ma una passeggiata aleatoria in due dimensioni è ricorrente, cioè, dati due punti qualsiasi x e y, la passeggiata Y_n passa per x e y infinite volte con probabilità 1. Pertanto per un punto campione ω opportunamente scelto esisterà una sottosuccessione infinita n_i tale che u(Y_n (ω)) = u(x) e una seconda sottosuccessione infinita k_i tale che u(Y_ki (ω)) = u(y). Inoltre un punto campione siffatto può essere scelto in modo che la successione u(Y(ω)) converga a Z(ω) e questo ovviamente implica u(x) = u(y).

Esempio tipico di martingala è una somma di variabili casuali indipendenti e la teoria delle martingale si è sviluppata largamente in analogia con questo caso classico.

Un'altra nozione che dipende dalle successioni stocastiche di σ-algebre è quella di tempo di arresto. Per un processo stocastico {X_n} un ‛tempo di arresto' è una variabile casuale T, che assume valore intero o infinito, tale che, per ogni n, l'evento (T ≤ n) appartiene alla σ-sottoalgebra di informazione generata da X_i, i ≤ n. Intuitivamente un tempo d'arresto formalizza il ragionamento per cui si decide se interrompere o no un gioco d'azzardo, sulla base di risultati precedenti. La variabile casuale X_T si dice arrestata. Tempi d'arresto sono stati studiati, nel contesto delle successioni di variabili casuali indipendenti, per determinare le strategie migliori nei giochi d'azzardo. Esiste in proposito una teoria molto estesa dovuta essenzialmente a Chow, Dubins, Robbins e Savage. Si possono utilizzare i tempi d'arresto per derivare da vecchi processi stocastici nuovi processi stocastici, per esempioY₁, Y₂, ... da X₁, X₂, ... scegliendo una successione opportuna di tempi d'arresto T₁ ≤ T₂ ≤ ... e ponendo Y_n = X_Tn. Per esempio, se X_n una martingala, si può dimostrare che Y_n è ancora una martingala sotto ipotesi deboli di finitezza.

8. Moto browniano

Sembra intuitivamente chiaro che la nozione di particella che si muove continuamente e a caso su una superficie liscia possa essere definita solo come un processo di limite partendo da una passeggiata aleatoria. Tuttavia il concetto preciso emerse lentamente soprattutto per merito di Bachelier, Einstein, Wiener, Lévy, Doob e Kac. Lo spazio campione Ω di un moto browniano a una dimensione (che si può facilmente generalizzare a più dimensioni) consta di tutte le funzioni continue su [0, ∞), che assumono valore zero nell'origine. La σ-algebra di eventi ℰ è generata dagli eventi elementari, indicati per α > β da E(α, β; t), secondo i quali una funzione continua prende, al tempo t, un valore compreso tra α e β. La probabilità dell'intersezione di n eventi siffatti, E(α₁, β₁; t₁) ⋂ ... ⋂ E(α_n, β_n ; t_n), è data dal seguente integrale multiplo:

ove 0 ⟨ t₁ ⟨ t₂ ⟨ ... ⟨ t_n e

D essendo una ‛costante di diffusione'.

In questa situazione la scelta della distribuzione normale è suggerita dal teorema del limite centrale per il passaggio al limite da una passeggiata aleatoria. Il fatto che queste probabilità siano coerenti è una conseguenza della proprietà di convoluzione della distribuzione normale:

per 0 ⟨ τ ⟨ t. Il fatto notevole che questa probabilità finitamente additiva definita su Ω sia di fatto numerabilmente additiva fu stabilito per la prima volta da N. Wiener che si servì dell'integrale di Daniell; essa viene oggi chiamata misura di Wiener.

Una definizione equivalente, ma dal punto di vista probabilistico più soddisfacente, di moto browniano si ottiene assegnando le distribuzioni congiunte della funzione a caso W(t), che chiameremo ‛posizione della particella al tempo t'. Basta specificare che W(t) ha incrementi indipendenti e che la distribuzione condizionata di W(t), data W(s) = a per un s ⟨ t, è normale con media a e varianza D(t − s) e pertanto con deviazione standard √−D(t − s). Il fatto che la deviazione standard dello spostamento di una particella che si muove ‛a caso' sia proporzionale alla radice quadrata del tempo impiegato per spostarsi è fondamentale e costituisce in un certo senso il contenuto concentrato del teorema del limite centrale.

Molti studi sono stati compiuti per calcolare le varie proprietà di una particella che si muove a caso in un moto browniano. Si può dimostrare, per esempio, che il cammino seguito da una particella non è mai differenziabile, con probabilità 1, sebbene esso soddisfi a una condizione di Hölder. Se T_a è la variabile casuale uguale al tempo corrispondente alla prima volta che la particella raggiunge un punto a ⟨ 0, si può dimostrare che T_a ha una distribuzione stabile con esponente 1/2. Di fatto (ponendo D = 1 da ora in poi)

Grosso modo a ogni proprietà geometrica di una passeggiata aleatoria, quali ad esempio il tempo di ritorno o il tempo del primo passaggio per l'origine, corrisponde una proprietà del moto browniano. Questo fatto intuitivo fu precisato per la prima volta da un notevole risultato di Donsker, noto con il nome di principio di invarianza, secondo il quale molte proprietà delle passeggiate aleatorie possono essere approssimate dalla ‛stessa' proprietà del moto browniano.

Siano X₁, X₂, ... variabili casuali indipendenti equidistribuite sullo stesso spazio campione Ω, con funzione di probabilità p′, media 0 e varianza 1. Poniamo S_n = X₁ + + ... + X_n e definiamo come sempre la funzione continua casuale S_(n)(t) per 0 ≤ t ≤ 1

S_(n)(i/n) = n^-1/2S_i per i = =, ..., n,

La funzione casuale S_n(t) può essere usata per definire una probabilità sullo spazio Ω₁ delle funzioni continue su [0,1] che si annullano nell'origine, in modo simile a quello in cui la misura di Wiener può essere calcolata mediante la funzione casuale W(t). Più precisamente, se A è un evento in Ω₁, si pone

μ_n(A) = p′({ω ∈ Ω′ : S_(n)(ω) ∈ A})

e si verifica che tutte le condizioni della teoria della misura sono soddisfatte.

Sia ϕ una funzione a valori reali su Ω₁, continua relativamente alla topologia della convergenza uniforme in Ω₁ Se μ è una misura di wiener ristretta a Ω₁, risulta

Questo è un enunciato del principio di invarianza di Donsker: eccone una tipica applicazione. La probabilità che, per 0 > x > 1, in una passeggiata aleatoria simmetrica di dimensione 1, si abbia, dati i primi n passi, un numero di passi minore o uguale a xn a destra dell'origine e maggiore o uguale a (1 − x)n a sinistra tende, per n → ∞, alla corrispondente probabilità del moto browniano:

Questa è la classica ‛legge dell'arcoseno'.

Il principio di invarianza ha dato spunto a molti studi sulla convergenza di misure in spazi di funzioni, ad opera soprattutto di Prohorov, di Skorohod e della scuola russa.

Non è un caso che la densità della distribuzione normale di varianza t sia la soluzione fondamentale dell'equazione del calore

Questo legame è il punto di partenza della teoria della diffusione, in cui viene definita una probabilità in uno spazio di funzioni sostituendo il nucleo gaussiano con la soluzione fondamentale dell'equazione alle derivate parziali di tipo parabolico - chiamata equazione di Fokker-Planck -

sotto ipotesi convenienti - anche se estremamente deboli - sulle funzioni a e b. In tal modo le proprietà della soluzione della (3) si riflettono in un processo stocastico descritto da una funzione casuale W(t), il ‛modello stocastico' per l'equazione alle derivate parziali (3). In quest'ordine di idee citiamo come esempio la celebre formula di Feynman-Kac. La soluzione fondamentale Q dell'equazione alle derivate parziali

cioè la soluzione che tende a δ(t) - funzione delta di Dirac - quando x → 0, è data dalla media condizionata relativa al moto browniano (sotto opportune condizioni su V), cioè

Questa formula ha dato l'avvio a studi estesi in fisica e in teoria spettrale.

Il primo a scoprire un legame tra il moto browniano e la teoria del potenziale fu Kakutani; indicheremo qui la sua originale argomentazione basata su analogie con le passeggiate aleatorie. In una passeggiata aleatoria in dimensione 1, siano A e B punti interi con A > B. Per A > n > B, sia u(n) la probabilità che la passeggiata aleatoria, che ha inizio in n, raggiunga B prima di raggiungere A. Con un semplice ragionamento si ottiene l'equazione alle differenze

u(n) = qu(n − 1) + pu(n + 1),

ove p è la probabilità di un passo a destra e q = 1 − p la probabilità di un passo a sinistra. L'analogo per un moto browniano in dimensione 2, cioè una coppia W(t) = (W₁(t), W₂(t)) di moti browniani indipendenti, si sviluppa nel modo seguente. Sia D un dominio liscio sul piano e sia f una funzione continua sulla frontiera ῼD di D. Per (x, y) ∈ D, definiamo la variabile casuale t(x, y) come il minimo tempo che un moto browniano con origine in (x,y) impiega a raggiungere ῼD. Sia u(x,y) = E(f(W_t(x,y))); applicando la legge delle probabilità composte si dimostra che u(x, y) soddisfa alla proprietà del valor medio, cioè che per ogni circonferenza di raggio r con centro in (x, y) si ha

Pertanto u(x, y) è una funzione armonica e quindi una soluzione del problema di Dirichlet per D, ossia una soluzione dell'equazione alle derivate parziali

uguale a f sulla frontiera di D.

Questa osservazione è stata il punto di partenza di una sistematica interpretazione probabilistica della teoria del potenziale per equazioni alle derivate parziali ellittiche del secondo ordine. Ricorderemo soltanto il seguente risultato dovuto a Doob. Se u è una funzione armonica nel piano e W(t) è un moto browniano in dimensione 2, u(W(t)) è una martingala indicizzata dal parametro continuo t. I teoremi di convergenza delle martingale possono essere così utilizzati per studiare le proprietà delle funzioni armoniche alla frontiera.

Malgrado ripetuti tentativi, fino ad ora non si è riusciti ad attaccare con successo con metodi probabilistici i problemi relativi alle equazioni alle derivate parziali di tipo iperbolico.

Poiché la funzione casuale W(t) può essere intuitivamente vista come un analogo continuo della somma di variabili casuali indipendenti, si sono fatti numerosi tentativi per definire un processo stocastico corrispondente, in un certo senso, alla derivata di W(t). Malgrado che W(t) non sia differenziabile con probabilità 1, nemmeno nel senso della media quadratica, Ito è riuscito a definire un integrale stocastico

ove f(t) è una funzione reale o addirittura - sotto condizioni particolari - una funzione casuale. Pertanto la derivata del moto browniano viene definita in un modo che ricorda la teoria delle distribuzioni di L. Schwartz. Essa corrisponde al fenomeno fisico noto come white noise, cioè a eccitazioni casuali discontinue nel tempo. L'integrale stocastico di Ito ha condotto allo sviluppo di un calcolo differenziale stocastico sul quale si sta ancora lavorando attivamente. Il fatto che l'incremento infinitesimo W(t + dt) − W(t) sia di ordine √−d−t conduce a regole di differenziazione sensibilmente diverse da quelle del calcolo differenziale ordinario. Per esempio, il differenziale di x(t) = exp W(t) risulta essere dx(t) = x(t)dW(t) + x(t)(dW(t))²/2.

9. Processi di Markov

Una ‛catena di Markov (stazionaria)' è una passeggiata aleatoria su un grafo arbitrario, i cui vertici vengono chiamati stati. A ogni lato che connette lo stato i allo stato j si associa una ‛probabilità di transizione' p_ij dallo stato i allo stato j, con la condizione che Σ_j p_ij = 1. Fisicamente si può immaginare una particella che a istanti discreti di tempo sia in uno stato definito e p_ij è la probabilità condizionata che la particella si trovi nello stato j al tempo n + 1, ammesso che sia nello stato i al tempo n. La matrice p_ij prende il nome di ‛matrice delle probabilità di transizione'. (In una catena di Markov non stazionaria, le probabilità di transizione dipendono dal tempo).

Lo spazio campione Ω di una catena di Markov è costituito, come per una passeggiata aleatoria, da successioni infinite di stati ciascuna delle quali rappresenta la ‛passeggiata' o ‛cammino' di una particella attraverso gli stati. Per gli stati prefissati i e j e il tempo prefissato n, un evento elementare è l'insieme di tutti i cammini per i quali la particella è nello stato i al tempo n e nello stato j al tempo n + 1. Le probabilità vengono assegnate mediante la regola delle probabilità composte.

Matematicamente una catena di Markov è completamente descritta dalla matrice P = (p_ij) delle probabilità di transizione e ci si potrebbe aspettare che la teoria spettrale di questa matrice stocastica contenga tutte le informazioni relative alla catena di Markov. Ciò accade effettivamente per le proprietà più semplici. Per esempio l'autovettore associato al più alto autovalore positivo di P esprime lo stato stazionario della catena e gli autovalori la cui norma è uguale al raggio spettrale di P forniscono informazioni sull'andamento periodico della catena. Tuttavia lo studio probabilistico delle catene di Markov ha fornito una quantità di nuovi concetti ben al di là di quanto possa fornire l'attuale teoria spettrale.

Più in generale un processo di Markov si può descrivere come una successione X_n di variabili casuali con la proprietà che p(X_n ∣ X_n-1, X_n-2, ...) = p(X_n ∣ X_n-1). Quando X_n ha valori interi, si ottiene una catena di Markov con probabilità di transizione stazionarie (supponendo che, indipendentemente da n, p_ij = p((X_n = j) ∣ (X_n-1 = i)), per n > 1). Definizioni analoghe possono introdursi per processi di Markov con parametri continui. La variabile casuale X₀ è assegnata arbitrariamente e rappresenta la posizione di partenza della particella.

Come esempio consideriamo il processo di diramazione. Una ‛particella' crea j nuove particelle con probabilità p_j e la creazione ha luogo a intervalli di tempo discreti. Gli stati sono il numero delle particelle in un tempo dato. Sia X_n il numero delle particelle al ‛tempo' n e siano Y₁, Y₂, ... le variabili casuali indipendenti equidistribuite con X₁. Risulta X_n = Y₁ + Y₂ + ... + Y_Xn-1, onde p_ij può essere calcolata mediante la regola delle probabilità composte.

Gli stati di una catena di Markov sono classificati secondo la possibilità di comunicazione tra di essi. Uno stato i si dice ‛ricorrente' se è uguale a 1 la probabilità che una particella con origine in i ritorni in i; altrimenti lo stato si chiama ‛transitorio'. Per uno stato ricorrente i, il tempo di ricorrenza T_i è la variabile casuale che dà il tempo del primo ritorno allo stato i e la sua speranza E(T_i) è il tempo medio di ricorrenza. Si può avere E(T_i) = ∞ per uno stato ricorrente. Sotto condizioni opportune sulla catena, la distribuzione di probabilità q_i sugli stati, Σ_i q_i = 1, con q_i proporzionale a E(T_i)^-1, dà lo stato stazionario; cioe se si pone una particella nello stato i con probabilità q_i e quindi si lascia scorrere la catena, al passo successivo la particella si troverà ancora allo stato i con probabilità q_i, per ogni stato i. Analiticamente questo significa che il vettore con componente q_i è l'autovettore della matrice P delle probabilità di transizione corrispondente all'autovalore 1. La teoria della probabilità, dunque, offre una formula esplicita per questo autovettore che va ben al di là della teoria classica di Perron-Frobenius delle matrici a elementi positivi.

La tendenza allo stato stazionario è espressa dal fatto che le potenze Pⁿ della matrice delle probabilità di transizione tendono a quella matrice le cui righe esprimono lo stato stazionario. Dal punto di vista probabilistico ciò significa che, indipendentemente dalla posizione iniziale, un gran numero di particelle che scorrono simultaneamente per la catena potranno trovarsi in proporzione a q_i nello stato i.

La struttura fine delle catene di Markov è stata studiata soprattutto tramite due tecniche: la prima estende la ‛teoria della prima e ultima uscita', o tempo di uscita, a insiemi arbitrari di stati facendo ricorso alla ‛teoria del rinnovo'.

La teoria del rinnovo è lo studio delle somme di variabili casuali positive indipendenti, ma può essere visualizzata nel modo migliore nel caso speciale di tempi di ricorrenza successivi indipendenti Ti⁽¹⁾, T_i⁽²⁾, ..., relativi allo stato i. Si utilizza il fatto che, quando la particella è ritornata allo stato i, il processo ricomincia, indipendentemente da quello che è successo prima, onde il termine ‛rinnovo'. I risultati principali, soggetti a ipotesi deboli di non periodicità, ma validi più in generale per variabili casuali a valori interi non negativi, sono i seguenti.

Sia u_n la probabilità che la particella si trovi nello stato i al tempo n. Lo stato i è transitorio se, e soltanto se, Σ_n u_n = u > ∞, nel qual caso la probabilità di tornare allo stato i è data dalla (u − 1)/u.

Quando lo stato i è ricorrente, le probabilità u_n convergono a E(T_i)^-1, l'inverso del tempo medio di ricorrenza. Questo risultato offre sovente un modo per calcolare lo stato stazionario.

La seconda tecnica consiste nell'uso sistematico dei tempi di arresto. Ciò ha condotto all'approfondimento dell'osservazione fenomenologica soggiacente alla teoria dei processi di Markov e precisamente ‛il futuro dipende dal tempo n, ma non da quanto è accaduto prima del tempo n'. Si intuisce che questa osservazione dovrebbe restare valida quando l'intero n viene sostituito da un tempo di arresto N, quando cioè per ogni k l'evento (N = k) appartiene alla ‛algebra generata da X₀, X₁, ... , X_k. Che ciò avvenga realmente è contenuto nella proprietà forte di Markov che ora esporremo. La probabilità di un evento dipendente da X_N, X_N+1, ... , condizionata rispetto agli X_n per n ≤ N, è uguale alla probabilità dello stesso evento, dipendente da X₀, X₁, ..., condizionata rispetto alla catena che comincia dallo stato X_N. In simboli

p((a₁ > X_N > b₁) ⋂ (a₂ > X_N+1 > b₂) ⋂ ... ∣ X_n, n ≤ N) =

=p((a₁> X₀ > b₁) ⋂ (a₂ > X₁ > b₂) ⋂ ... ∣ X₀ = X_N).

Lo studio dei processi generali di Markov con spazio di stati arbitrario e parametro temporale continuo è concettualmente simile a quello delle catene di Markov, tuttavia richiede un apparato analitico più potente. La matrice delle probabilità di transizione è sostituita da un semigruppo a un parametro P^t, t > 0, di operatori lineari che conservano la positività in uno spazio di funzioni opportunamente ordinato, tali che P^t₁ = 1, ove 1 è la funzione identicamente uguale a 1. Quando gli operatori P^t sono realizzati da una famiglia di nuclei

la proprietà di semigruppo P^t+s = P^tP^s diventa l'equazione di Chapman-Kolmogorov

La tendenza allo stato stazionario è espressa dal fatto che il limite

è, sotto condizioni opportune, una soluzione dell'equazione Ag = 0, ove A è il generatore infinitesimale del semigruppo P^t. Il generatore ha molte proprietà in comune con un operatore alle derivate parziali ellittico del secondo ordine. Seguendo la traccia del caso classico del moto browniano in dimensione d, ove

si può associare a un processo di Markov generale un analogo probabilistico della teoria del potenziale, in cui il ruolo delle funzioni armoniche è sostenuto dalle soluzioni dell'equazione Ag = 0.

Un caso intermedio studiato a fondo è quello della classe di processi di Markov con parametro temporale continuo, ma spazio di stati discreto. I motivi che hanno indotto ad approfondire questi studi sono diversi; le applicazioni più importanti si hanno nei modelli di popolazione, nei problemi di manutenzione di apparecchiature e, soprattutto, nei problemi di code. In quest'ultimo caso gli stati vengono abitualmente associati al numero dei clienti in attesa davanti ai diversi terminali e le probabilità di transizione sono determinate dall'organizzazione dei servizi - o ‛disciplina della coda' - in ogni fila. Consideriamo come esempio uno dei casi più semplici.

Supponiamo che un sistema telefonico consista di r terminali. Si suppone che le telefonate in arrivo siano casuali nel tempo e quindi distribuite alla Poisson con intensità λ. Una volta iniziata una conversazione, la probabilità che essa abbia termine al tempo dt è μdt, ove μ è un dato parametro. Se tutti i terminali sono occupati, le nuove telefonate in arrivo si mettono in lista d'attesa finché non si sia liberata una linea. Questo dà origine a una catena di Markov con un parametro continuo, ove lo stato i significa che esistono esattamente i chiamate in atto o in attesa.

Il semigruppo di probabilità di transizione P^t non viene calcolato direttamente. Di fatto è molto più facile calcolare il generatore infinitesimale A mediante un sistema di equazioni differenziali della forma q′(t) Aq(t), ove q(t) è un vettore la cui componente i-esima q_i(t) è la probabilità che al tempo t la coda sia nello stato i. Dai dati precedenti si deduce facilmente l'uguaglianza

q′_i(t) = − (λ + rμ)q_i(t) + λq_i-1(t) + rμq_i+1(t),

dalla quale, integrando un sistema di equazioni differenziali a coefficienti costanti in un numero infinito di incognite, si ottiene il semigruppo P^t. Lo stato stazionario della catena, e precisamente la soluzione q di Aq = 0, ossia (λ + rμ)q_i = λq_i-1 + rμq_i-1, risulta essere

e

e può essere normalizzato a una distribuzione di probabilità solo se λ/μ > r. Se questa condizione non è soddisfatta, la linea d'attesa cresce oltre ogni limite.

La derivazione indicata precedentemente di un sistema di equazioni differenziali - e quindi il calcolo esplicito del generatore infinitesimale - mediante un'analisi infinitesimale delle transizioni è caratteristica di tutte le catene di Markov con tempo continuo e spazio di stati discreto. La teoria di catene siffatte è uno dei capitoli che hanno avuto maggiore successo nella storia della probabilità. Anche nello studio delle catene di Markov a parametro discreto spesso è risultato analiticamente utile considerare l'analogo a parametro continuo. Per concludere ricorderemo la proprietà caratteristica dei tempi d'attesa esponenziali: se H_i è il tempo d'attesa per lasciare lo stato i, H_i è sempre distribuito esponenzialmente.

Uno dei più recenti sviluppi della teoria dei processi di Markov è la teoria dei campi di Markov casuali, la quale formalizza il concetto, già familiare ai fisici, di ‛interazione col piu vicino'. Sull'insieme Z^d dei punti con coordinate intere consideriamo l'insieme Ω di tutte le funzioni che prendono valori 0 o 1. Un campo di Markov casuale è una misura di probabilità p su Ω che soddisfa, oltre a ipotesi di non banalità, anche alla condizione seguente, per ω ∈ Ω e x ∈ Z^d;

p(ω(x) = 1 ∣ tutti valori di ω su Z^d − x) =

=p(ω(x) = 1 ∣ ω(y) per gli y più vicini a x).

Si suppone inoltre che le probabilità siano invarianti per traslazione. Il fenomeno della transizione di fase in meccanica statistica è strettamente collegato al fatto che, date certe condizioni, può esserci più di un campo casuale di Markov dotato di date probabilità condizionate. Nel caso in cui

cioè quando le probabilità condizionate dipendono soltanto dal numero, ma non dalla posizione, degli stati eccitati vicini, si può dimostrare che p_k = ar^k-d/(l + ar^k-d), per opportuni parametri a e r.

10. Processi gaussiani

Consideriamo ora variabili casuali a valori complessi e a quadrato integrabile. L'insieme di tutte queste variabili casuali è uno spazio di Hilbert rispetto al prodotto interno

⟨ X, Y > = E(XÇ).

Diversi concetti probabilistici hanno i loro corrispettivi più deboli nello spazio di Hilbert delle variabili casuali a quadrato integrabile e spesso questi analoghi ‛geometrici' sono più trattabili. Per esempio, la nozione di variabili casuali indipendenti si indebolisce nella nozione di variabili casuali non correlate. Due variabili casuali X e Y si dicono ‛non correlate' se

E((X − E(X))( −Y−−−−E−(−Y−))) = 0.

Allo stesso modo il processo abitualmente complesso di prendere medie condizionate si indebolisce in quello molto più semplice della proiezione ortogonale, spesso su un sottospazio a dimensione finita. Una successione stocastica si indebolisce, in uno spazio di Hilbert, nel concetto familiare di risoluzione spettrale. Doob ha suggerito l'uso delle specificazioni ‛in senso stretto' per il concetto probabilistico puro e in ‛senso lato' per l'analogo concetto della geometria dello spazio di Hilbert.

È un fatto notevole, tuttavia, che i due punti di vista coincidano nel caso particolare più importante: quello di un processo gaussiano. Si dice che una d-pla Y = (Y₁, ... , Y_d) di variabili casuali ha una ‛distribuzione congiunta normale', se esiste una c-pla di variabili casuali indipendenti X = (X₁, ..., X_c), ciascuna con distribuzione normale con media 0 e varianza 1 e una matrice A, c × d, tale che

Y 0 a + XA

per un opportuno vettore a. Un insieme di variabili casuali si chiama ‛processo gaussiano' (o ‛congiuntamente normale') quando ogni sottoinsieme ha una distribuzione congiunta normale. Il moto browniano è un esempio di processo gaussiano.

Variabili casuali congiuntamente normali sono indipendenti se, e soltanto se, sono non correlate. Più in generale, la distribuzione congiunta delle variabili congiuntamente normali X₁, ... , X_n può essere espressa razionalmente mediante i prodotti interni ⟨ X_i, X_j >. Pertanto lo studio dei processi gaussiani si riduce allo studio di insiemi di vettori nello spazio di Hilbert L²(Ω). In questo modo alcune nozioni classiche della geometria dello spazio di Hilbert hanno eleganti interpretazioni probabilistiche mediante i processi gaussiani. A titolo di esempio - forse il più significativo - descriveremo l'interpretazione probabilistica del teorema spettrale per gli operatori unitari. Un processo gaussiano stazionario, per il quale, cioè, le probabilità congiunte sono invarianti per traslazione, è completamente determinato - assumendo per semplicità che tutte le variabili casuali abbiano media 0 - dalla sua ‛autocorrelazione' ρ:

ρ(t) = E(X_s+tÙ_s).

L'autocorrelazione è una funzione definita positiva; se è anche continua, per il teorema di Bochner essa è la trasformata di Fourier di una misura positiva sulla retta reale; cioè

La misura μ si chiama ‛spettro di potenza' del processo.

Da questo risultato possiamo dedurre un teorema di rappresentazione per processi gaussiani stazionari. Sia Z(λ) una famiglia di variabili casuali indicizzata da un parametro reale λ. Per un intervallo reale I = [λ₁, λ₂) poniamo Z(I) = Z(λ₂) − Z(λ₁). In questo modo si definisce sulla retta reale una misura finitamente additiva avente per valori variabili casuali e, come nella costruzione dell'integrale di Riemann, possiamo definire

per una funzione f soddisfacente opportune condizioni di integralità. Ogni processo gaussiano stazionario può essere rappresentato da un integrale siffatto; esiste cioè Z(λ) tale che

Inoltre il processo stocastico Z(λ) è ancora gaussiano e le variabili casuali Z(I₁) e Z(I₂) sono non correlate quando gli intervalli I₁ e I₂ sono disgiunti. Infine E( ∣ Z(I) ∣ ²) = μ(I) per ogni intervallo I.

Abbiamo parlato precedentemente del problema della predizione per un processo stazionario indicizzato da un parametro reale. Se tale processo stazionario è gaussiano, il problema di calcolare la media condizionata

E(X_n ∣ X_n-1, X_n-2, ...)

si riduce a cercare una proiezione in L²(Ω), che si chiama il miglior operatore di predizione di X_n dato il passato. Il calcolo di questa proiezione si può eseguire ricorrendo all'analisi armonica. Nello spazio di Hilbert L²(R, μ) delle funzioni a quadrato integrabile sulla retta reale rispetto allo spettro di potenza, sia L^- il sottospazio generato dalle funzioni e^ikλ per tutti gli interi k ≤ 0. Il problema della predizione per processi gaussiani stazionari consiste nel trovare una funzione f(λ) in L^- tale che l'integrale

sia minimo. Questo problema venne risolto esplicitamente e indipendentemente da Kolmogorov e da Wiener.

Mediante l'interpretazione in termini di processi gaussiani, ogni spazio di Hilbert può essere rappresentato come un sottospazio chiuso G di L²(Ω) nel quale ogni sottoinsieme finito di variabili casuali è congiuntamente normale o, brevemente, un sottospazio gaussiano. Un tale sottospazio G può essere inoltre scelto massimale relativamente alla proprietà di essere un sottospazio gaussiano. Sotto queste condizioni, ogni operatore unitario nello spazio di Hilbert G si estende univocamente a una trasformazione che conserva le misure dell'intero spazio L²(Ω).

Queste e altre simili considerazioni suggeriscono l'esistenza di un analogo della risoluzione spettrale e della teoria della molteplicità spettrale per classi di processi stocastici più generali dei processi gaussiani. Tuttavia l'argomento non è ancora sufficientemente esplorato.

11. Fondamenti filosofici della probabilità

Fin dalle sue origini, la nozione di casualità ha procurato non poco imbarazzo sia ai matematici sia ai filosofi. Le numerose applicazioni teoriche e pratiche, ottenute con un insieme di concetti mal compresi, rendono ancora più invitante un'indagine sui fondamenti della teoria della probabilità, anche se i risultati conseguiti finora sembrano addirittura aumentare le nostre perplessità.

Il Kollektif di von Mises, che cercò di definire la casualità di una successione i cui elementi sono 0 e 1 come una proprietà di una sola successione piuttosto che come concetto insiemistico, si scontrò con le nozioni sviluppate da Kolmogorov tra il 1930 e il 1940 nell'ambito di una ricerca sui fondamenti della teoria della misura. Il tentativo di von Mises fu poi abbandonato per la sua scarsa maneggevolezza. Più recentemente, tuttavia, lo stesso Kolmogorov, e contemporaneamente Chaitin, Solomonoff e altri, hanno riportato alla luce e modernizzato le idee di von Mises, snellendole e rendendole più attuali con l'uso di tecniche di logica matematica, specialmente con la teoria della ricorsività, che erano state sviluppate negli anni successivi, rendendo così più accettabile la visione pionieristica di von Mises.

L'idea sta nel formalizzare il giudizio del buon senso secondo il quale la successione 11111111 ... è meno casuale, per esempio, della successione 01100010 ... , definendo la casualità di una successione mediante la sua ‛complessità'. A sua volta questa viene definita come la misura della difficoltà di definire l'n-esimo termine ricorsivamente mediante i precedenti, o come la lunghezza della ‛programmazione' ricorsiva più piccola dell'n-esimo termine mediante il precedente.

Il concetto di casualità come complessità si è rivelato più efficace nella teoria della calcolabilità che in quella della probabilità.

Un tentativo più promettente di alterare i fondamenti della probabilità che appartengono alla teoria degli insiemi potrebbe avere origine nell'analisi delle ipotesi soggiacenti alla nozione di evento. Molti autori hanno affrontato questa impresa spinti dalla scarsa maneggevolezza della nozione di evento di probabilità zero, o dalle necessità della meccanica quantistica. In ambedue i casi si è intrapreso uno studio del reticolo soggiacente, col proposito di eliminare i punti campione la cui struttura, dal punto di vista della teoria della misura, è complicata, o di usare un reticolo più generale, che non soddisfi alla legge distributiva A ⋃ (B ⋃ C) = (A ⋃ B) ⋂ (A ⋃ C).

Carathéodory, nella sua opera postuma Mass und Integral, che venne apprezzata al suo giusto valore solo parecchi anni dopo la morte dell'autore, riuscì a sviluppare l'algebra delle variabili casuali, di fatto tutta la teoria della misura, senza mai servirsi della nozione di punto campione. Nell'impostazione di Carathéodory si parte da uno ‛spazio' campione costituito da una σ-algebra astratta di Boole B i cui elementi sono chiamati eventi. Una probabilità è una funzione numerabilmente additiva definita su una σ-algebra di Boole siffatta con valori nell'intervallo [0,1], che si annulla soltanto sull'elemento nullo. Carathéodory mostrò che l'algebra delle variabili casuali potrebbe essere sviluppata in questo contesto rarefatto senza fare ricorso alla nozione di funzione misurabile, giustificando così l'intuizione dei probabilisti, secondo cui l'identificazione delle variabili casuali con le funzioni misurabili è soltanto una questione di convenienza.

Brevemente possiamo dire che una variabile casuale è ridefinita come un'applicazione dai numeri reali a uno spazio dei campioni B, in simboli t → [X > t], soddisfacente alle tre seguenti proprietà:

Addizione e moltiplicazione possono essere definite in modo che l'insieme delle variabili casuali costituisca un anello commutativo rispetto a queste operazioni; inoltre si possono definire anche i concetti della teoria della probabilità classica, come ad esempio quelli di ‛media', ‛composizione', ecc., mediante funzioni analitiche reali.

Come esempio del metodo di Carathéodory, diamo la definizione di somma e di prodotto di due variabili casuali non negative X e Y, cioè di variabili casuali per le quali [X ≤ t] e [Y ≤ t] sono l'evento nullo ogniqualvolta sia t ≤ 0. La somma è la variabile casuale Z = X + Y definita dalla

e similmente il prodotto P = XY è definito dalla

La definizione di Carathéodory di variabile casuale ricorda la definizione di risoluzione spettrale di un operatore autoaggiunto in uno spazio di Hilbert; questa analogia non passò inosservata a von Neumann, il quale, certamente in modo indipendente, dedicò gran parte della sua attività matematica a stabilire un'opportuna struttura per la logica - e, insieme a questa, per la probabilità - della meccanica quantistica. È ancor oggi opinione largamente diffusa che il principio di indeterminazione di Heisenberg sia collegato, mediante un'argomentazione mai del tutto chiarita, alla mancanza di una legge distributiva nel reticolo soggiacente degli eventi, la quale viene sostituita da una legge modulare più debole, secondo la quale la legge distributiva sussiste ancora se due qualsiasi degli eventi A, B, C sono comparabili. Sarebbe pertanto comodo poter prendere un reticolo modulare (certamente un σ-reticolo) come sostituto in meccanica quantistica della nozione di spazio campione e definire in meccanica quantistica variabili casuali nello stesso modo usato da Carathéodory nel caso classico. Sfortunatamente tutti i tentativi di sviluppare l'algebra delle variabili casuali in questo contesto non hanno avuto successo e non si è mai riusciti nemmeno a definire la somma di variabili casuali. L'idea di von Neumann per ovviare a questa difficoltà fu di prendere un opportuno reticolo di sottospazi chiusi di uno spazio di Hilbert e di definire una funzione dimensione normalizzata mediante successivi dimezzamenti, in analogia con la costruzione di un isomorfismo tra il processo di Bernoulli e il processo uniforme sull'intervallo [0,1].

Riassumeremo la costruzione di von Neumann, avvertendo tuttavia il lettore che i dettagli delle dimostrazioni sono talora molto delicati.

Sia H uno spazio di Hilbert separabile; scegliamo due sottospazi chiusi, ortogonali, isomorfi, H₁ e H₂, e due isometrie parziali E₂₁ : H₁ → H₂ e E₁₂ : H₂ → H₁ tali che E₂₁E₁₂ coincida con l'identità su H₂ e con l'operatore nullo altrove e E₁₂E₂₁ coincida con l'identità su H₁ e con l'operatore nullo altrove. Sia ora E_ii la proiezione ortogonale su H_i, così che E₁₁ + E₂₂ = I, l'operatore identità. Le E_ij si comportano come unità di matrici. Esiste pertanto un isomorfismo fra l'algebra delle matrici due-per-due A = (a_ij) e un'algebra di operatori limitati su H, dato dalla

Questa costruzione può essere iterata. Allo stesso modo sì decompone H₁ in H₁₁ + H₁₂ e, combinando le due composizioni, sì ottiene un insieme di operatori E⁽i²j⁾ che obbediscono alle stesse identità delle unità di matrici quattro-perquattro; si ottiene così un isomorfismo A = (a_ij) → L_A⁽²⁾ dell'algebra delle matrici quattro-per-quattro definita dalla stessa formula precedente e così via per l'algebra delle matrici 2ⁿ per 2ⁿ. Arrivati all'n-esimo passaggio, si definisce la traccia (normalizzata)

Il fatto è che questa definizione di traccia, ristretta ai 2ⁿ sottospazi ortogonali corrispondenti all'n-esimo passaggio, risulta indipendente da n e si può passare al limite e prendere la chiusura in un'opportuna topologia per gli operatori in uno spazio di Hilbert (la topologia debole per gli operatori), ottenendo così un'algebra di operatori detta ‛fattore iperfinito'. I sottospazi chiusi dello spazio di Hilbert dotati della proprietà che la proiezione ortogonale loro associata appartiene al fattore iperfinito formano un reticolo modulare e la traccia della loro proiezione ortogonale è un analogo di una funzione probabilità. Un operatore autoaggiunto appartenente al fattore iperfinito è l'analogo di una variabile casuale e la sua risoluzione spettrale è l'analogo di una distribuzione di probabilità. La traccia è l'analogo della media. Pertanto la somma e il prodotto di variabili casuali sono ‛automaticamente' definiti.

Seguendo queste analogie, si può definire una ‛probabilità non commutativa' che è molto vicina alle idee della meccanica quantistica. Ci limiteremo qui a ricordare la suggestiva scoperta di I. Segal di un analogo ‛non commutativo' della distribuzione normale, che Segal chiamò distribuzione di Clifford.

La probabilità non commutativa mostra chiaramente la mancanza di categoricità dell'interpretazione di probabilità mediante una σ-algebra di Boole e mette in rilievo un importante problema filosofico ancora non risolto: quello di determinare tutte le possibili strutture matematiche che realizzano famiglie di distribuzioni congiunte, come nel teorema di consistenza di Kolmogorov.

La nozione di probabilità in uno spazio campione di eventi è stata criticata da un altro punto di vista. Una valutazione della probabilità comincia da precedenti ipotesi di distribuzioni di probabilità, argomento questo sottolineato in modo convincente dagli statistici bayesiani e soprattutto da De Finetti. Si sostiene quindi che è la probabilità condizionata, piuttosto che la probabilità, che dovrebbe essere assunta come concetto di base. A. Rényi è stato il primo a formalizzare un sistema assiomatico in cui la probabilità condizionata viene assunta come concetto primario. Uno ‛spazio di probabilità condizionata' sull'insieme Ω è dato dagli elementi seguenti: una σ-algebra di Boole di eventi ℰ, con sottoinsieme distinto ℱ ⊆ ℰ chiuso rispetto alle unioni e non contenente l'insieme vuoto, e una funzione p(E ∣ F), definita sulle coppie di eventi E ∈ ℰ e F ∈ ℱ, detta probabilità condizionata dell'evento E rispetto a F, soddisfacente ai tre assiomi seguenti:

p(E ∣ F) ≥ 0 e p(F ∣ F) = l per E ∈ ℰ e F ∈ ℱ;

per ogni F ∈ ℱ fissato, p(E ∣ F), come funzione di E, è una misura numerabilmente additiva su ℰ;

se E ∈ ℰ, F, G ∈ ℱ, F ⊆ G e p(F ∣ G) > 0, risulta

p(E ∣ F) = p(E ⋂ F ∣ G)/p(F ∣G).

Allo stato attuale, gli spazi di probabilità condizionata di Rényi hanno trovato applicazione soprattutto nella probabilità geometrica. È facile prevedere tuttavia che questa nozione sarà resa più duttile ed efficace quando verrà sostituito lo spazio dei campioni Ω con un analogo probabilistico della nozione di topos, che si è dimostrata così efficace in geometria. Ciò eliminerebbe definitivamente l'indesiderato spazio ‛universale' dei campioni Ω.

Sarebbe infine grave negligenza non ricordare i profondi legami esistenti tra i fondamenti della probabilità e quelli della statistica. L'eterno problema è quello di trovare, e di giustificare filosoficamente, criteri per attribuire a priori significato a un insieme di dati. Su questo scoglio sono naufragate tutte le ricerche filosofiche sui fondamenti della probabilità e della statistica.

(Gli autori ringraziano la dott. S.A. Joni e il dott. S. M. Roman per la loro collaborazione ai primi paragrafi della prima stesura e ringraziano inoltre il dott. Baclawski e i dott. M. Pratelli e M. Cerasoli per la revisione critica del manoscritto).

bibliografia

Aitken, A. C., Statistical mathematics, Edinburgh 1957.

Billingsley, P., Convergence of probability measures, New York 1968.

Breiman, L., Probability, Reading, Mass., 1968.

Carathéodory, C., Mass und Integral und ihre Algebraisierung, Basel 1956.

Chow, Y. S., Robbins, H., Siegmund, C., Great expectations; the theory of optimal stopping, Boston 1971.

Chung, K. L., Markov chains, Berlin 1967.

De Finetti, B., Teoria della probabilità, 2 voll., Torino 1970.

Doob, J. L., Stochastic processes, New York 1953.

Dubbins, L.E., Savage, L. J., How to gamble if you must, New York 1965.

Dunford, N., Schwartz, J. J., Lnear operators, vol. I, New York 1958, vol. II, New York 1963, vol. III, New York 1971.

Erdös, P., Spencer, J., Probabilistic methods in combinatorics, New York 1974.

Fano, R. M., Transmission of information, New York 1961.

Feller, W., An introduction to probability theory and its applications, vol. I, New York 1968, vol. II, New York 1971.

Fine, T. L., Theories of probability, New York 1973.

Friedman, N. A., Introduction to ergodic theory, New York 1970.

Halmos, P. R., Lectures on ergodic theory, Tōkyō 1956.

Hille, E., Phillips, R. S., Funcitonal analysis and semigroups, Providence 1957.

Kac, M., Probability and related topics in the physical sciences, New York 1959.

Kac, M., Statistical independence in probability, analysis and number theory, Buffalo 1959.

Kappos, D. A., Probability algebras and stochastic spaces, New York 1969.

Kendall, D. G., Harding, E. F. (a cura di), Stochastic analysis, New York 1973.

Kendall, D. G., Harding, E. F., Stochastic geometry, New York 1974.

Kendall, D. G., Moran, P. A., Geometrical probability, London 1963.

Kingman, J. F. C., Regenerative phenomena, New York 1972.

Kolmogorov, A. N., Grundbegriffe der Wahrscheinlichkeitsrechnung, Berlin 1933.

Lévy, P., Théorie de l'addition des variables aléatoires, Paris 1937, 1954².

Lévy, P., Processus stochastiques et mouvement brownien, Paris 1965.

Loève, M., Probability theory, Princeton 1963.

McKean, H. P., Stochastic integrals, New York 1969.

Mehta, M. L., Random matrices, New York 1967.

Meyer, P. A., Probability and potentials, Waltham 1966.

Moran, P. A. P., An introduction to probability theory, Oxford 1968.

Neveu, J., Martingales à temps discret, Paris 1972.

Preston, C. L., Gibbs states on countable sets, Cambridge 1974.

Rényi, A., Foundations of probability, San Francisco 1970.

Rényi, A., Probability theory, Amsterdam 1970.

Santalò, L. A., Integral geometry and geometric probability, Reading, Mass., 1976.

Segal, I. E., A non-commutative extension of abstract integration, in ‟Annals of mathematics", 1953, LVII, pp. 401-457.

Segal, I. E., Tensor algebras over Hilbert spaces, in ‟Transactions of the American Mathematical Society", 1956, LXXXI, pp. 106-134.

Segal, I. E., Tensor algebras over Hlibert spaces, II, in ‟Annals of mathematics", 1956, LXIII, pp. 160-175.

Spitzer, F., Principles of random walk, Princeton 1964.

Wiener, N., Collected works, vol. I, Cambridge 1976.

Wiener, N., Siegel, A., Rankin, B., Martin, W. T., Differential space, quantum systems and prediction, Cambridge 1976.