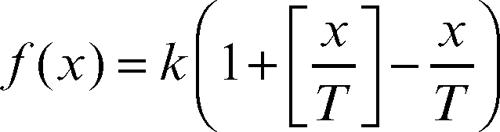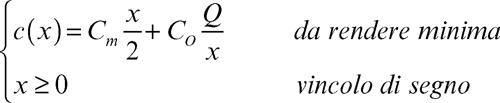scorte, problema delle

scorte, problema delle

scorte, problema delle in ricerca operativa, problema di ottimizzazione riguardante la gestione delle scorte di magazzino. Questo tipo di problema, seppur di carattere aleatorio, dietro opportune semplificazioni produce un modello matematico di tipo deterministico, che risulta comunque utile per effettuare la necessaria programmazione nella gestione delle scorte. Per semplificare il problema da un punto di vista matematico si suppone che:

• il consumo della merce sia uniforme nel tempo e non si prevedano fatti congiunturali, tra i quali, per esempio, scioperi, malattie dei dipendenti, alti e bassi del mercato ecc.;

• si conosca a priori il fabbisogno di merce per l’intero periodo preso in considerazione e, quindi, la quantità di merce fissa da ordinare ogni volta;

• il tempo intercorrente tra il momento di esaurimento delle scorte e l’arrivo della nuova merce sia nullo;

• i costi per ogni ordinazione siano costanti per tutto il periodo di riferimento.

Sulla base di queste ipotesi, una funzione che descrive il fenomeno (giacenza in magazzino in funzione della quantità di merce da ordinare x) è

in cui k rappresenta un fattore moltiplicativo, che, nel caso specifico, corrisponde alla quantità di merce da ordinare, T indica il periodo, cioè l’intervallo di tempo che intercorre tra un’ordinazione e la successiva e [ ] indica la → funzione parte intera. Il grafico della funzione ƒ(x) ha un andamento a “dente di sega”, che evidenzia il fatto che a esaurimento delle scorte (punti di minimo, sull’asse delle ascisse) si ha un immediato reintegro (punti di massimo, corrispondente alla quantità ordinata o da ordinare).

I costi relativi alla gestione delle scorte sono suddivisi in due categorie:

• costi di ordinazione: costi relativi alla gestione amministrativa delle scorte e indipendenti dalla quantità ordinata, quali, per esempio, telefono, personale di segreteria, posta, cancelleria ecc.;

• costi di magazzinaggio: sono più in generale i costi relativi all’immobilizzazione di capitali, all’affitto del magazzino, all’assicurazione contro i danni, all’eventuale deterioramento della merce ecc.

Il costo relativo alla merce può invece essere considerato una costante, poiché si conosce il quantitativo totale di merce da ordinare ogni volta e il relativo costo, che si suppone rimanga invariato per tutto il periodo di tempo preso in considerazione. In un problema di gestione delle scorte l’obiettivo è quindi quello di rendere minimi i costi, equilibrando la necessità di ridurre il numero delle ordinazioni e nello stesso tempo contenere i costi per la gestione del magazzino. Indicando con Q il fabbisogno complessivo di merce, x il quantitativo di merce da ordinare ogni volta, C_O il costo per ogni ordinazione, C_m il costo unitario per spese di magazzino, il numero complessivo di ordinazioni da effettuare è n = Q/x. I costi complessivi per la gestione del magazzino sono uguali al prodotto tra il costo unitario e la giacenza media, cioè la quantità di merce che mediamente si trova nel magazzino, che è uguale a x/2, cioè alla media aritmetica tra il valore massimo (x) e quello minimo (0).

Indicando con c(x) la funzione del costo totale, cioè il costo derivante dalla somma del costo di magazzinaggio con quello dell’ordinazione, si ha il seguente modello matematico per l’analisi del problema delle scorte:

La → funzione obiettivo è del tipo

formula

e ha come grafico un’iperbole con asintoti l’asse delle ordinate e la retta di equazione y = ax.

La funzione c(x) ha un minimo per

formula

e il costo totale dell’ordinazione in corrispondenza di questo minimo è uguale a

formula

Nella realtà non esiste il caso del reintegro delle scorte a tempo nullo. La gestione reale degli approvvigionamenti avviene effettuando l’ordine di reintegro quando le scorte sono giunte a un prefissato livello, detto livello di riordino. Tuttavia, in assenza di fattori perturbativi, l’ipotesi di semplificazione matematica non toglie nulla alla soluzione del problema, poiché il grafico della funzione con reintegro delle scorte a tempo nullo e quello della funzione con riordino effettuato a un certo livello di sicurezza sono identici a meno di una traslazione.

PROBLEMA DELLE SCORTE