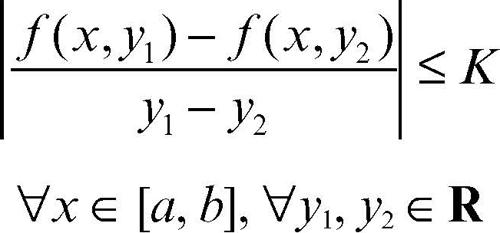Cauchy, problema di

Cauchy, problema di

Cauchy, problema di (per un’equazione differenziale ordinaria di ordine n) è il problema che consiste nell’assegnazione del valore della soluzione e delle sue derivate fino all’ordine n − 1 in corrispondenza di un fissato valore della variabile indipendente. Se l’equazione è nella forma normale, ovvero y⁽ⁿ⁾ = ƒ(x, y, y′, …, y⁽ⁿ⁻¹⁾), e si assegnano i valori

l’equazione stessa fornirà il valore della derivata n-esima nel punto x₀:

Geometricamente, il problema di Cauchy per un’equazione del primo ordine y′ = ƒ(x, y) corrisponde alla richiesta che la soluzione passi per un determinato punto (x₀, y₀); per un’equazione del secondo ordine esso impone che la soluzione passi per un dato punto con una determinata tangente ecc. Fisicamente, per un’equazione del secondo ordine che regola il moto di un punto materiale, il problema consiste nell’assegnare posizione e velocità iniziale del punto. Per questo il problema di Cauchy è detto anche problema dei valori iniziali. Se la funzione ƒ è continua, in un aperto A ⊆ Rⁿ⁺¹ e il punto

è elemento di A, il problema di Cauchy ammette almeno una soluzione (teorema di Peano); questa è unica se ƒ soddisfa una condizione di Lipschitz uniforme rispetto alle variabili y, y′,…, y⁽ⁿ⁻¹⁾, e in particolare questo è il caso se ƒ è di classe C¹. L’intervallo di esistenza della soluzione non può essere stabilito a priori, se non con ulteriori ipotesi. Per esempio, data l’equazione y′ = 2xy ², il problema di Cauchy y(0) = 1/a² ammette la soluzione y = 1/(a² − x ²), definita nell’intervallo (−a, a), mentre il problema y(0) = −1/a² ammette la soluzione y = −1/(a² + x ²), definita su tutto R.

Una condizione sufficiente perché qualsiasi problema di Cauchy per l’equazione y′ = ƒ(x, y) ammetta soluzione unica in un assegnato intervallo [a, b] contenente x₀ è che ƒ(x, y) sia continua nella striscia S = [a, b] × R, soddisfi la condizione di Lipschitz in y uniformemente rispetto a x, ovvero esista una costante K > 0:

e che in S risulti |ƒ(x, y)| ≤ A|y| + B, con A, B ≥ 0 (teorema di esistenza e unicità in grande).

Per l’equazione in forma non normale F(x, y, y′ ) = 0, lo studio dell’esistenza e unicità della soluzione del problema di Cauchy y(x₀) = y₀ si esegue valutando mediante il teorema di Dini la possibilità di risolvere l’equazione rispetto a y′, quindi applicando i precedenti teoremi a ciascuna delle equazioni in forma normale che si possono ottenere. Per esempio, l’equazione (y′ )² + y ² + 1 = 0 non ammetterà alcuna soluzione, mentre per la (y′ )² + y ² − 1 = 0 il problema di Cauchy y(0) = 0 fornisce i due valori y′ (0) = ±1; da ciascuno di essi si ottiene un’equazione in forma normale

che fornisce una soluzione (y = ±sinx). Analogamente il problema di Cauchy y(0) = 0 per siny′ = 0 ammette le infinite soluzioni y = kπx, con k intero. Nell’impossibilità di applicare il teorema di Dini lo studio si fa più complicato. Per esempio, il problema di Cauchy y(0) = 1 per l’equazione (y′ )² + y ²−1 = 0 dà le soluzioni y = cosx e y ≡ 1, tra loro tangenti, mentre il problema y(0) = 0 per xy′ − 2y = 0 ammette come soluzioni tutte le parabole y = Cx ², con C arbitraria (→ integrale singolare).