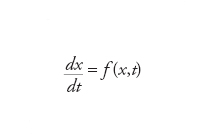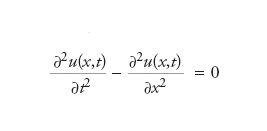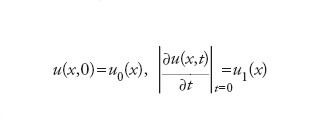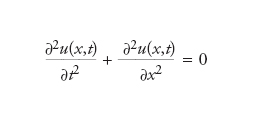problema di Cauchy
problema di Cauchy
Nel contesto delle equazioni differenziali di evoluzione, problema di determinare la soluzione corrispondente a un’assegnazione del dato iniziale. In alcuni casi è ovvio quali sia il dato iniziale necessario e sufficiente a individuare la corrispondente soluzione: per es., nel caso della equazione del primo ordine alle derivate ordinarie
con f(x,t) funzione data, il dato iniziale x(0) è chiaramente sufficiente a determinare univocamente la soluzione x(t) per t>0 se la quantità f(x,t) è ben definita per x=x(0) e t=0; e la soluzione x=(t) risulta ben definita fino a quando la funzione f(x,t) si mantiene a sua volta ben definita per x=x(t). Si noti che in questa formulazione supponiamo che la variabile indipendente t sia uno scalare, laddove la variabile dipendente x potrebbe anche essere un oggetto a più componenti, per es., un vettore o una matrice. Nel caso di più variabili indipendenti, e dunque di equazioni alle derivate parziali, la definizione di problema di Cauchy è analoga nella misura in cui esiste una variabile indipendente rispetto alla quale l’equazione in questione si presta a esser considerata come ‘equazione di evoluzione’; ma in tal caso la determinazione di quali siano i dati iniziali necessari e sufficienti a caratterizzare univocamente la soluzione del problema di Cauchy può essere men che banale, richiedendo la formulazione di un apposito teorema. Può inoltre darsi il caso in cui la soluzione corrispondente al dato iniziale esiste ed è unica, ma manifesta drastiche variazioni in corrispondenza di piccole variazioni del dato iniziale: in questi casi si dice che il problema di Cauchy, per l’equazione in questione, è ‘mal posto’ e, viceversa, se una tale patologia non si verifica, si dice che il problema di Cauchy è ‘ben posto’. Per es., il problema di Cauchy è ben posto per l’equazione lineare iperbolica
con dati iniziali
dove le funzioni u0(x), u1(x) sono assegnate e ben definite per ogni valore della variabile indipendente x; laddove è mal posto il problema di Cauchy con analoghi dati iniziali ma per l’equazione lineare ellittica
