Malfatti, problema di

Malfatti, problema di

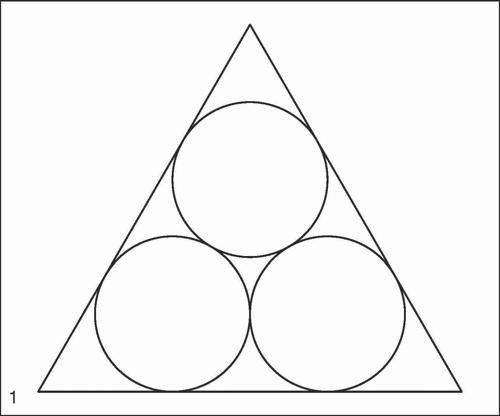
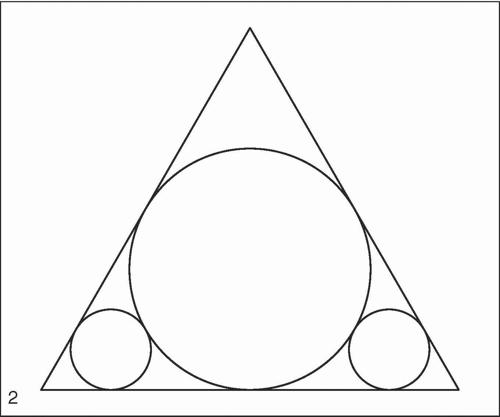
Malfatti, problema di problema posto nel 1803 da G. Malfatti; nella formulazione attuale, consiste nel tracciare, internamente a un triangolo, tre circonferenze ognuna tangente a due lati del triangolo, tra loro mutuamente tangenti e tali da racchiudere la massima area. Tale problema è anche detto marble problem (problema del marmo) perché trae origine dalla richiesta, fatta a Malfatti stesso da un marmista, di ricavare da un blocco di marmo, a forma di prisma retto a base triangolare, tre colonne in modo tale da minimizzare lo scarto. Essendo le altezze delle colonne uguali, il problema si riduce a un problema di ottimizzazione di geometria piana; in questa forma era già stato posto dal matematico giapponese Chokuen Ajima (1732-1798) per cui, talvolta, la sua soluzione è anche indicata come teorema di Ajima-Malfatti. Malfatti si convinse erroneamente che il problema equivalesse a quello di costruire tre circonferenze all’interno di un dato triangolo, tangenti tra loro e tangenti a due lati del triangolo (circonferenze di → Malfatti); in realtà, la loro costruzione non soddisfa la richiesta di massimizzare l’area complessiva dei tre cerchi. Infatti, nel 1930, il matematico inglese Herbert W. Richmond (1863-1948) mostrò il seguente controesempio: in un triangolo equilatero, la circonferenza inscritta e altre due circonferenze a essa tangenti esternamente e costruite in due delle tre regioni prossime ai vertici del triangolo (fig. 2) racchiudono un’area complessiva maggiore di quella racchiusa dalle circonferenze di Malfatti (fig. 1). Si dimostra inoltre che, mentre le circonferenze di Malfatti non costituiscono mai la soluzione del marble problem, la costruzione di Richmond ne costituisce la soluzione generale.