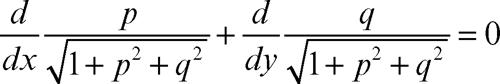Plateau, problema di

Plateau, problema di

Plateau, problema di consiste nella ricerca delle superfici che, tra quelle che hanno un determinato contorno, abbiano l’area minima. Il problema prende il nome da Joseph Antoine Ferdinand Plateau (1801-1883), fisico belga che attorno al 1850 studiò le superfici formate da bolle di sapone aventi un contorno prefissato, costituito da fili di ferro. Si tratta dunque, se si suppone la superficie in forma cartesiana, di minimizzare il funzionale

dove p e q sono le derivate parziali della funzione incognita u = u(x, y), che assume un valore assegnato sul bordo ∂Ω di Ω. L’equazione di → Eulero-Lagrange relativa a tale funzionale è

Si tratta di un’equazione del secondo ordine, non lineare, la cui soluzione non può essere determinata analiticamente nel caso generale, anche se numerose soluzioni particolari sono state date a partire da Eulero (nel 1744), J.-B. Meusnier de la Place, H. Scherk. La condizione equivale a dire che la superficie ha curvatura media nulla, o, come si dice, è una superficie minima (nome dato da J.-L. Lagrange, 1760); viceversa una superficie minima può non avere area minima: G. Monge dimostrò tuttavia che ogni superficie minima differenziabile che abbia come bordo una curva chiusa semplice è anche di area minima.