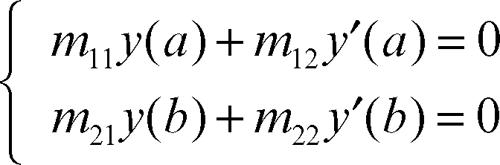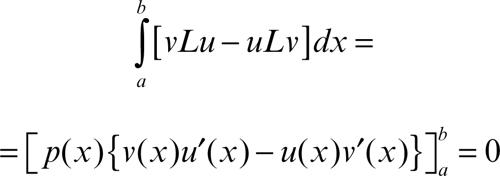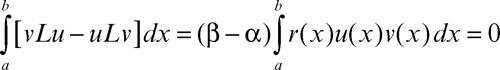Sturm-Liouville, problema di
Sturm-Liouville, problema di
Sturm-Liouville, problema di problema ai limiti omogeneo per un’equazione differenziale del secondo ordine, consistente nella determinazione di una soluzione che soddisfi condizioni ai limiti del tipo a1y(a) + a2y′ (a) = 0, b1y(b) + b2y′ (b) = 0, dove a e b sono punti assegnati nell’intervallo dove è definita l’equazione e ai e bi sono numeri reali assegnati.
Si consideri l’operatore differenziale lineare
nel sottospazio V di L2(a, b) formato dalle funzioni regolari che soddisfano le condizioni
(con la precisazione che tali condizioni non si banalizzino in 0 = 0). La forma di L è detta autoaggiunta (→ equazioni differenziali, problemi ai limiti per) perché per ogni coppia di funzioni u e v ∈ V risulta (v, Lu) = (u, Lv), precisamente:
Se ora le funzioni u e v ∈ V soddisfano l’equazione differenziale Ly + λr(x)y = 0, con r(x) > 0 in [a, b], la prima in corrispondenza di λ = α, la seconda di λ = β ≠ α, risulta
Ciò si interpreta dicendo che le due autosoluzioni u e v, corrispondenti agli autovalori distinti α e β, sono tra loro ortogonali rispetto al peso r(x). È lecito ammettere che r(x) si annulli in qualche punto di [a, b]; inoltre le condizioni ai limiti si possono generalizzare qualora il fattore p(x) si annulli in uno o entrambi gli estremi.
Si mostra che, sotto opportune ipotesi, vi sono infiniti autovalori e che le corrispondenti autosoluzioni formano un sistema completo, nel quale è possibile eseguire uno sviluppo di → Fourier generalizzato di una generica funzione appartenente a L2r(x)(a, b).