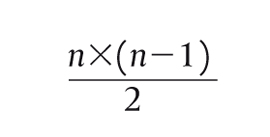problema
problema
Quando la risposta a una domanda non è immediata
Ogni volta che si deve prendere una decisione e la soluzione non è subito disponibile, allora si ci pone un problema, che può essere di qualunque natura (affettivo, economico, di salute, di geometria), può riguardare la vita privata o professionale di una persona; oppure può essere un problema sociale. A seconda della natura e della generalità del problema, cambia la strategia adottata per risolverlo
Qui c’è un problema!
Un problema nasce quando si vuole raggiungere una meta, un obiettivo, ma non è disponibile una risposta pronta, una strategia automatica. Esempi di problemi sono: cercare la strada migliore per andare da un punto a un altro della città; calcolare quanto legno occorre per costruire una libreria di date dimensioni; scegliere l’operatore telefonico più conveniente per i nostri usi; valutare quanto tempo occorre per prepararsi la mattina prima di uscire. Di un problema occorre innanzitutto individuare gli elementi essenziali, trascurando quelli che non sono utili per risolverlo. In particolare, bisogna individuare:
• che cosa vogliamo esattamente sapere, cioè qual è il risultato che ci aspettiamo per fare una scelta, per prendere una decisione;
• quali sono i dati a nostra disposizione, cioè gli elementi certi e necessari che consentono di arrivare al risultato, cioè alla risoluzione;
• quali sono le condizioni, cioè le relazioni tra i dati e le incognite, le limitazioni, i vincoli.
Si ricorre quindi a un modello che contenga tutti e soli gli elementi essenziali e permetta di trovare un algoritmo di risoluzione.
Analisi di un caso
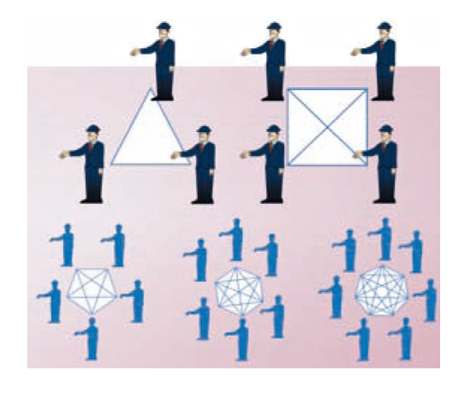
Consideriamo il seguente problema: «n persone si incontrano e ognuno stringe la mano a ogni altro. Quante strette di mano si scambiano?». Innanzitutto che cosa significa «n persone»? Questo è un modo di presentare il problema in generale: non ci si chiede quante strette di mano si danno due, tre, mille persone, ma si vuole risolvere il problema indipendentemente dal loro numero. Si usano perciò lettere al posto dei numeri: si considera un modello matematico di tipo algebrico, e anche il risultato non sarà un numero, bensì una formula, cioè una regola generale e quindi un algoritmo. Si può quindi procedere per tentativi o analizzando alcuni casi particolari.
Per esempio, se si incontrano 2 persone, si ha 1 stretta di mano; se si incontrano 3 persone, le strette di mano sono 3. Può essere utile, a questo punto, rappresentare il problema con un diverso modello, di tipo geometrico: si rappresentano le persone con punti e le strette di mano con tratti che uniscono i punti. Con 3 e 4 persone si ha la situazione illustrata nella figura; tale figura mostra come si può proseguire con i modelli per 5, 6, 7 persone.
Si possono riassumere le informazioni raccolte in una tabella, come quelle disegnate sulla lavagna. Così è possibile cogliere una regolarità: aumentando di 1 il numero di persone, il numero di strette di mano aumenta ogni volta di più. Otteniamo la nuova rappresentazione disegnata in basso sulla lavagna.
Ragionando sui casi particolari fin qui considerati, si può arrivare alla conclusione:
• ogni persona stringe la mano a tutte le altre persone meno che a sé stesso. Se le persone sono n, ogni persona dà quindi (n1) strette di mano. Sembrerebbe allora che esse siano n×(n-1);
• tuttavia, la stretta di mano di A a B, è la stessa che B dà ad A e quindi tale numero va diviso per 2.
La formula richiesta è perciò:
n. strette di mano= formula
Problemi e modelli
Proprio perché si utilizzano modelli per risolvere problemi, è possibile che lo stesso modello (o addirittura la stessa formula) valga per problemi di diversa natura.
Per esempio, il problema delle strette di mano può essere riformulato in altri modi; quanti sono i lati e le diagonali di un poligono di n lati? Quante sono le linee telefoniche necessarie per collegare n impianti fissi? In questo caso si parla di problemi isomorfi.
La soluzione di un problema, che permette di passare da una situazione iniziale di incertezza a uno stato finale in cui si può dire che il problema è risolto, è quindi strettamente connessa all’uso di un adeguato modello che può essere algebrico, geometrico, oppure semplicemente uno schema, una tabella o qualunque altro tipo di rappresentazione.