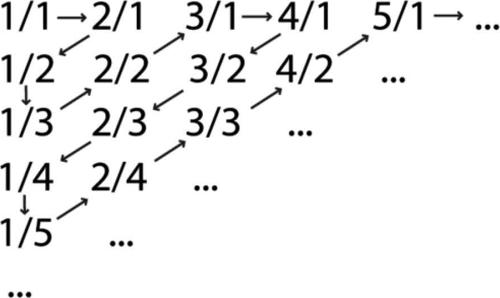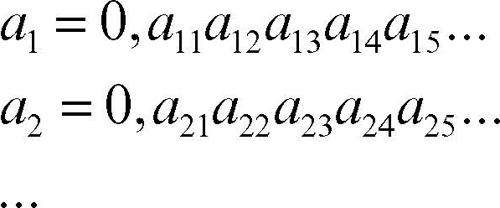Cantor, procedimento diagonale di

Cantor, procedimento diagonale di

Cantor, procedimento diagonale di detto anche argomento diagonale di Cantor, è il metodo per dimostrare che l’insieme dei numeri razionali Q è numerabile (primo procedimento diagonale) e per dimostrare che l’insieme dei numeri reali R non è numerabile (secondo procedimento diagonale). Il primo procedimento opera sullo schema

in cui ogni razionale positivo compare almeno una volta. Scrivendo i numeri nell’ordine indicato dalle frecce, previa omissione di quelli equivalenti a frazioni già elencate, si ottiene

che ordina in successione tutti i numeri razionali positivi. Poiché, per definizione, l’insieme dei valori di una successione è un insieme numerabile, segue che l’insieme dei numeri razionali positivi è numerabile. Il procedimento può essere riadattato all’insieme di tutti i numeri razionali Q e mostra che esso stesso è numerabile.

Il secondo procedimento individua, per ogni successione {a_n} di numeri reali compresi tra 0 e 1, un numero x, compreso tra 0 e 1, che non compare nella successione costruita {a_n}. Si supponga infatti di considerare una tale successione, avendo scritto ogni numero reale in forma decimale (i simboli a_ij qui indicano cifre):

Si costruisce allora il numero x = 0, x₁x₂x₃x₄x₅ ... nel modo seguente: per ogni indice i, si pone la cifra x_i uguale a una cifra diversa da 0, da 9 e da a_ii. Il numero x costruito in questo modo differisce da ogni termine della precedente successione almeno per la sua i-esima cifra decimale; dunque x non compare nella successione e perciò l’intervallo reale [0, 1], contenendo almeno un elemento che non compare nella lista precedente, non è un insieme numerabile. Di conseguenza, contenendo questo intervallo, nemmeno l’insieme R dei numeri reali è numerabile.