programmazione lineare
programmazione lineare
programmazione lineare settore della ricerca operativa che si occupa di ottimizzare problemi lineari, cioè aventi come modello una funzione obiettivo lineare, sottoposta a vincoli lineari. In campo economico, per esempio, il problema può consistere nell’ottimizzazione dell’uso delle risorse disponibili per la realizzazione di prodotti con caratteristiche diverse, ma che utilizzano le stesse risorse: uno stesso macchinario, gli stessi mezzi di trasporto, lo stesso gruppo di operai, lo stesso magazzino ecc. La programmazione lineare tratta il caso in cui la funzione da minimizzare sia lineare nelle variabili, per esempio del tipo ƒ(x1, x2, …, xn) = c1x1 + … + cnxn con le variabili soggette a m vincoli lineari del tipo ai1x1 + … + ainxn ≤ bi, i = 1, … , m, e a vincoli di segno xi ≥ 0. Un modello di problema di programmazione lineare è in sostanza composto da:
• una funzione obiettivo, lineare in tutte le variabili che vi compaiono;
• un insieme di vincoli, costituiti da equazioni o disequazioni lineari;
• un dominio dei vincoli, che, per ciascuna variabile, indica i valori che essa può assumere.
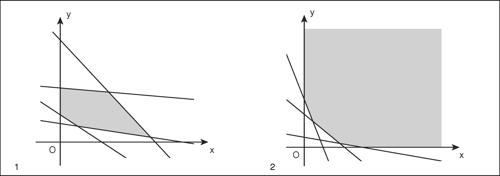
Le variabili che compaiono in una funzione obiettivo sono dette variabili di azione. La regione dello spazio a n dimensioni delimitata dai vincoli è detta regione ammissibile: si tratta in genere di un poliedro (o, più in generale, un politopo se n > 3). Soluzione ammissibile del problema è ogni punto della regione ammissibile; una soluzione ammissibile si dice ottima se in corrispondenza la funzione obiettivo assume il suo valore minimo (massimo). Un problema di programmazione lineare, sia esso di massimo o di minimo, può essere risolto in generale con il metodo del → simplesso. L’algoritmo del simplesso consiste in una ricerca guidata della soluzione ottima sull’insieme dei vertici della regione ammissibile, mediante la quale, da un vertice assegnato, ci si sposta su un vertice adiacente in modo che in corrispondenza di esso la funzione obiettivo assuma un valore non inferiore (superiore) a quello assunto nel vertice di partenza. Replicando la procedura, la soluzione ottima, se esiste finita, è raggiunta in un numero finito di passi, inferiore a quello corrispondente all’esame di tutti i vertici, mentre, mediante opportune verifiche, è possibile riconoscere se la soluzione ottima non esiste o non è unica. In particolare, per i problemi di minimo può essere utilizzato il principio di dualità, che consente di trasformare lo studio di un problema di minimo nello studio di un problema di massimo, aventi la medesima soluzione ottima. Se un problema di programmazione lineare dipende da sue sole variabili o da più variabili riconducibili a due, allora si può anche risolvere per via grafica e, se i vincoli sono tra loro compatibili, il dominio dei vincoli è rappresentabile con una regione convessa chiusa o aperta.
I vertici della poligonale che delimita il campo di scelta costituiscono le soluzioni ammissibili di base, cioè quelle particolari soluzioni ammissibili tra cui individuare la soluzione ottima. Le soluzioni ammissibili sono tutte quelle soluzioni che appartengono al campo di scelta.
Per la risoluzione di problemi di programmazione lineare si fa riferimento al seguente principio: il valore ottimo della funzione obiettivo, quando esistente, si trova su uno dei vertici della poligonale che racchiude il campo di scelta. In sostanza, il principio fa riferimento al fatto che se esiste una soluzione ammissibile, allora esiste una soluzione ammissibile di base e se esiste una soluzione ottima, allora esiste anche una soluzione ottima che è di base. Una funzione obiettivo lineare in due variabili rappresenta l’equazione di un piano nello spazio a tre dimensioni e questo piano può essere sezionato con piani paralleli al piano Oxy, così da individuare un insieme di rette le cui proiezioni sul piano Oxy sono un fascio di rette parallele. Considerata la funzione z = ax + by + q, l’equazione ax + by = k, al variare del parametro k, rappresenta quindi un fascio di rette parallele, che, nel caso specifico, sono le rette di livello (→ curva di livello) del piano z sul piano Oxy. Nel caso in cui la funzione z rappresenti un profitto oppure un costo, tali rette di livello assumono un particolare significato:
• linea di isoprofitto, che passa per tutti quei punti del piano le cui coordinate producono un medesimo profitto;
• linea di isocosto, che passa per tutti quei punti del piano le cui coordinate producono un medesimo costo.
Per esempio, data la funzione z = 2x + 3y, i punti A(3, 3) e B(6, 1) appartengono entrambi alla retta di equazione 2x + 3y = 15 e 15 è proprio il valore che la funzione z assume in ciascuno dei punti A e B. Per una equazione del tipo z = ax + by, il vettore u = (a, b) è perpendicolare alle rette del fascio delle linee di livello e rappresenta il cosiddetto “verso delle z crescenti”, per cui nella risoluzione di un problema di programmazione lineare in due variabili è sufficiente studiare l’andamento delle rette di livello. Per individuare la soluzione ottima di un problema di programmazione lineare in due variabili, si individua quindi la retta di livello per la quale è minore o maggiore il valore del termine noto, rispettivamente per funzioni obiettivo da minimizzare o massimizzare.