proiettivita omologica

proiettivita omologica

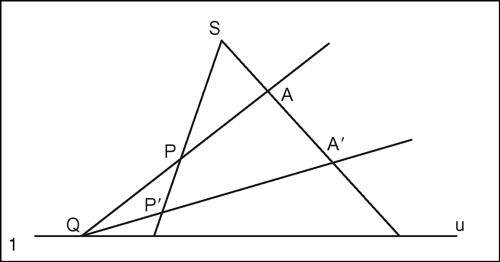
proiettività omologica o omologia proiettiva piana, particolare trasformazione proiettiva del piano definita come → omografia di un piano proiettivo in sé avente un punto S fisso e una retta u luogo di punti uniti. Costruttivamente è definita nel modo che segue. Fissati nel piano una retta u, detta asse della proiettività omologica, un punto S ∉ u, detto centro di proiezione, un punto A e il suo corrispondente A′, allineati con S, a ogni punto P del piano, diverso da S, si fa corrispondere il punto P′, così ottenuto:

• si traccia la retta AP e si determina il punto Q in cui tale retta interseca l’asse u;

• si traccia la retta SP;

• si traccia la retta QA′ che interseca la retta SP nel punto P′, corrispondente di P nella proiettività omologica.

La proiettività omologica così definita ha le seguenti proprietà:

• è una collineazione;

• conserva i birapporti;

• tutti i punti dell’asse u sono punti uniti (la retta u è una retta fissa);

• una retta parallela all’asse si trasforma in una retta parallela all’asse.

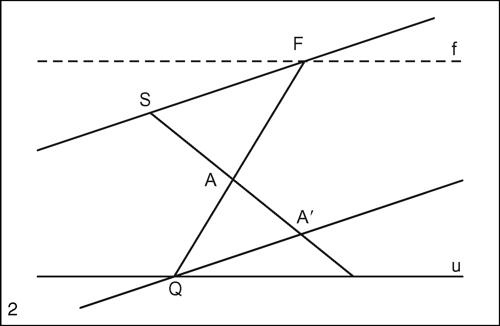
Vi sono nel piano punti i cui corrispondenti F′ nella proiettività omologica sono punti all’infinito. I punti con tale proprietà sono detti punti di fuga. Il luogo dei punti di fuga è una retta parallela all’asse della proiettività omologica u. La retta ƒ è detta retta di fuga ed è la retta che ha per immagine nella proiettività omologica la retta impropria del piano. Un punto di fuga e la retta di fuga sono detti anche, rispettivamente, punto limite e retta limite.