proiezione cartografica
proiezione cartografica
proiezione cartografica metodo con cui si rappresenta graficamente la superficie terrestre o una sua porzione (proiezione geografica), secondo una scala opportuna e con la maggiore esattezza possibile. Le proiezioni cartografiche che più si avvicinano alla realtà sono quelle riportate su di un globo, che rappresenta con sufficiente corrispondenza il geoide terrestre; ogni altra rappresentazione è approssimata perché una superficie sferica non può essere sviluppata su un piano. Tuttavia si possono costruire proiezioni che permettano di ridurre al minimo le deformazioni rispetto alla reale superficie terrestre rappresentata e che consentano di mantenere inalterate le caratteristiche almeno di punti e luoghi essenziali in rapporto allo scopo cui la carta deve rispondere. I metodi grafici usati sono quelli della geometria; per sviluppare la rappresentazione si utilizzano linee direttrici ausiliarie quali il fascio di rette della rosa dei venti e il reticolato dei meridiani e paralleli; questi ultimi si tracciano sulla carta perché il loro andamento permette di interpretare e di comprendere il modo secondo cui la carta è costruita. Data l’impossibilità di mantenere inalterati contemporaneamente gli angoli, le aree e le distanze reali si deve scegliere quale delle tre grandezze debba essere conservata: si mantiene la corrispondenza degli angoli quando sia necessario conservare la forma delle coste e gli angoli di rotta, come nelle carte nautiche; in tal caso le proiezioni si dicono conformi o isogoniche. Si mantengono inalterate le aree quando si vogliano rappresentare fenomeni geografici e in tal caso le proiezioni si dicono equivalenti o omolografiche. Si mantengono inalterate le distanze nelle carte stradali e simili, e in questo caso le proiezioni si dicono equidistanti.
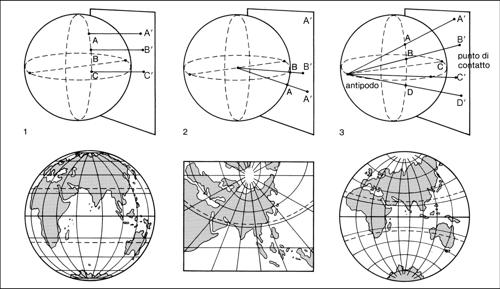
Tenendo conto delle proiezioni cartografiche più usate, si possono avere proiezioni puramente geometriche, dette prospettiche semplici o azimutali, o zenitali che si ottengono proiettando la zona da rappresentare su di un piano tangente la zona stessa, partendo da un punto di vista che può essere posto nel centro del globo terrestre (proiezione gnomonica), alla estremità del diametro tracciato ortogonalmente al centro del piano (proiezione stereografica), in un punto posto all’infinito rispetto alla congiungente il centro del globo e l’estremo del diametro precedente (proiezione ortografica), in un punto esterno rispetto al diametro precedente (proiezione scenografica). Dalle diverse combinazioni di questi tipi, si possono ottenere 12 proiezioni prospettiche semplici e un certo numero di proiezioni prospettiche più complesse; nelle prime si ottiene un’approssimazione relativa di tutte e tre le grandezze (angoli, aree, distanze); nelle seconde si può mantenere inalterata una delle tre grandezze fondamentali (per esempio, le proiezioni zenitali possono essere equivalenti o equidistanti). Altre proiezioni geografiche permettono di mantenere rigorosamente esatte o l’equivalenza o l’equidistanza e contemporaneamente di conoscere gli effettivi scostamenti dai valori delle altre due grandezze: tali sono le proiezioni di sviluppo, suddivise in cilindriche, coniche, pseudocilindriche, pseudoconiche; esse si ottengono sviluppando la superficie di un cilindro o di un cono considerati tangenti al globo terrestre e sul quale sono stati proiettati tutti i punti della zona che si vuole rappresentare.
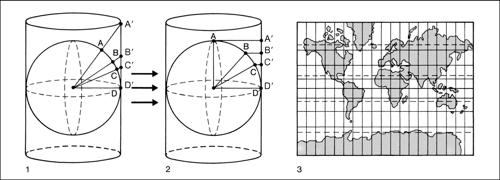
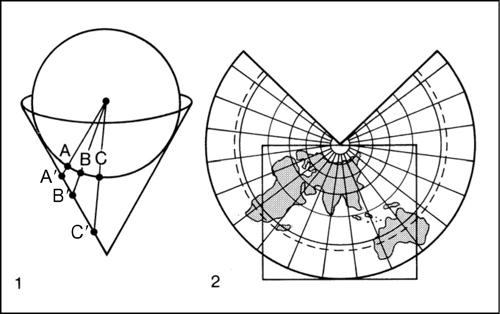
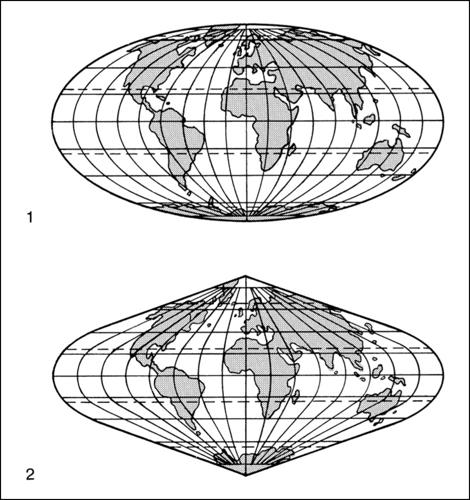
Fra le proiezioni cilindriche, particolare interesse hanno quelle del geografo greco Marino di Tiro (i-ii secolo d.C.), di G.D. Cassini, di G. Mercatore, di J.H. Lambert. Nella proiezione di → Mercatore, detta anche cilindroisogonica, meridiani e paralleli sono rappresentati con rette parallele ortogonali tra loro. Le distanze tra meridiani sono sempre uguali al grado equatoriale, mentre per i paralleli aumentano in rapporto inverso al coseno della latitudine; ne deriva una esagerazione nel senso sudnord dell’ampiezza delle aree le quali però conservano una perfetta similitudine con le zone corrispondenti. Tale proiezione è molto vantaggiosa per la navigazione in quanto la linea lossodromica taglia meridiani e paralleli sempre con lo stesso angolo. Le proiezioni coniche si prestano bene a rappresentare porzioni della superficie terrestre perché mettono bene in evidenza, scegliendo opportunamente il meridiano centrale della carta, i particolari della zona che si vuole rappresentare. La più semplice proiezione conica, detta conica vera, è costruita ponendo tangente al meridiano centrale della zona un cono retto; ne risulta che il meridiano centrale è rettilineo, gli altri meridiani convergono al vertice del cono con angoli uguali tra loro. Il parallelo centrale mantiene la sua lunghezza vera e, come tutti gli altri paralleli, è rappresentato da un arco di circonferenza; ogni parallelo risulta più corto e più curvo a mano a mano che ci si avvicina al polo, rappresentato esso pure da un arco; le maglie del reticolo diventano pertanto trapezi a basi più o meno curve a seconda della scala della carta. Tra le più note proiezioni coniche vi sono quelle del cartografo francese Guillaume Delisle (1675-1726), che compose un planisfero nel quale rappresentò solo ciò che risultava da rilevazioni sicure, correggendo notevolmente il modo di raffigurare la Terra che si usava sino allora, quella conforme di Lambert (→ Lambert, proiezione conica conforme di) e quella del geografo e astronomo tedesco Pietro Apiano (1495-1552). Di uso particolare sono le proiezioni pseudocilindriche e pseudoconiche ricavate dalle cilindriche e coniche mediante opportune modifiche; tra le prime, le più interessanti sono quella di K.B. Mollweide, nella quale i meridiani hanno forma ellittica via via più accentuata verso i bordi della carta e i paralleli sono linee rette (→ Mollweide, proiezione di), e quella di Hammer-Aitoff, che sviluppa l’intera superficie terrestre su di una ellisse e prende il nome dal militare Ernst von Hammer (1884-1957) e dal geografo russo David Aleksandrovič Aitoff (1854-1933). Tra le seconde, quella del cartografo francese Rigobert Bonne (1727-1795), nella quale i meridiani e i paralleli sono delle curve e le distanze tra meridiani lungo tutti i paralleli corrispondono alle distanze reali; quella di Sanson-Flamsteed, nella quale equatore e meridiano centrale sono ortogonali e suddivisi in parti equivalenti, i paralleli sono tutti linee rette e i meridiani archi di una sinusoide (per tale motivo è detta anche proiezione sinusoidale); tale proiezione venne definita dal cartografo nonché ingegnere militare francese Nicolas Sanson (1600-1667), spesso considerato il fondatore della cartografia moderna, e successivamente adattata dall’astronomo inglese John Flamsteed (1646-1719), primo direttore dell’Osservatorio di Greenwich (si veda anche → cartografia).