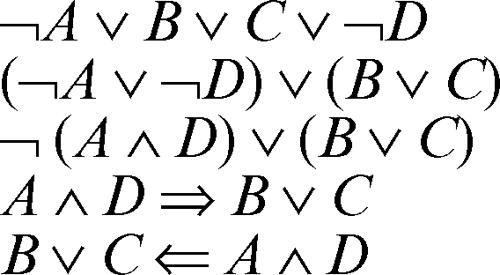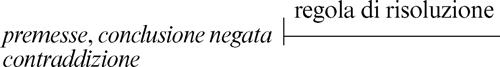PROLOG

PROLOG

PROLOG acronimo di programmation en logique (programmazione logica), indica un linguaggio di programmazione elaborato nel 1972 nell’ambito dell’università di Aix-Marseille sulla base dell’impostazione teorica del matematico e logico inglese R. Kowalski. È usato in vari contesti come l’→ intelligenza artificiale o la gestione di database di grandi dimensioni. Le istruzioni di un programma in prolog sono particolari scritture logiche, alla cui definizione si perviene attraverso l’uso dei connettivi e delle regole del calcolo dei predicati. Si definisce come letterale una proposizione costituita da una lettera che indica una variabile enunciativa (letterale positivo) o dalla sua negazione (letterale negativo): una proposizione C è un letterale, come pure la proposizione ¬C, il primo positivo e il secondo negativo. Utilizzando le regole di equivalenza logica stabilite nel calcolo degli enunciati, è possibile trasformare una qualsiasi proposizione composta in un’altra, a essa logicamente equivalente, contenente soltanto la negazione ¬, la congiunzione ⋀ e la disgiunzione ⋁. Una qualsiasi proposizione può essere riscritta in modo equivalente in → forma normale congiuntiva e, utilizzando le leggi di → De Morgan, in → forma normale disgiuntiva, cioè come disgiunzione generalizzata di sottoproposizioni, ciascuna delle quali è una congiunzione generalizzata di letterali. Si definisce clausola una disgiunzione generalizzata di letterali: può essere, quindi, un letterale singolo, una disgiunzione di letterali, ma può anche essere priva di letterali e in questo caso si parla di clausola vuota. Ogni forma proposizionale viene trasformata in un insieme di clausole e per le clausole si utilizza poi una particolare notazione (detta notazione di → Kowalski) così costruita: si raggruppano i letterali negativi in fondo alla clausola; si inserisce una freccia invertita dopo il gruppo di letterali positivi; si elimina il connettivo della negazione; si sostituisce ogni disgiunzione con una virgola. Per esempio la clausola ¬A ⋁ B ⋁ C ⋁ ¬D viene riscritta come B, C ← A, D e la si legge in questo modo: «B o C se A e D». La virgola è letta come disgiunzione se posta a sinistra del simbolo ← e come congiunzione se posta alla sua destra, in base alla seguente catena di equivalenze logiche:

Una scrittura del tipo ← A, B va interpretata come una negazione e sarà letta «non (A e B)», essendo tale clausola la riscrittura, in questa notazione, di ¬A ( ¬B.

La notazione a clausole offre un metodo efficiente per stabilire la verità di una proposizione composta a partire da quella delle proposizioni che la compongono. In particolare, il tentativo di automatizzare un sistema di deduzione ha portato a mettere a punto un sistema basato su una sola regola di inferenza, detta regola di risoluzione, che si applica però soltanto a formule espresse a clausole e che da due clausole genitori consente di ottenere una nuova clausola, detta clausola risolvente. Tale sistema è detto sistema di risoluzione-refutazione. Esso non utilizza una procedura diretta, così come la deduzione naturale, del tipo

ma una procedura diversa così schematizzabile:

Poiché da premesse vere si deduce una conclusione vera, se alle premesse si aggiunge la negazione della conclusione, si genera una contraddizione; quindi, l’insieme delle premesse più la negazione della conclusione va refutato. Questo sistema, facilmente automatizzabile, oltre a essere applicato al calcolo degli enunciati, può essere applicato al calcolo dei predicati, che prevede scritture con variabili. Tuttavia, occorre aver precedentemente trasformato una forma predicativa in una forma a clausole e opportunamente esteso la regola di risoluzione al calcolo dei predicati. Tale estensione non è immediata; per questo è spesso sufficiente far ricorso a clausole in cui al più un letterale è positivo, cioè che contengono al più una sola conclusione: sono queste le cosiddette clausole di → Horn. L’uso delle clausole di Horn, pur non togliendo nulla alla capacità espressiva del formalismo logico, rende molto più semplice il processo di automatizzazione delle inferenze logiche: molti dei modelli utilizzati in intelligenza artificiale sono esprimibili con clausole di questo tipo. Nella terminologia di tali clausole: una regola è una clausola con una singola conclusione e una o più condizioni; un fatto è una clausola con una singola conclusione, ma senza alcuna condizione; un goal è una clausola senza conclusione e indica ciò che si vuole dimostrare. La seguente è per esempio una sequenza di forme predicative (con il predicato che antecede gli argomenti) che sono clausole di Horn:

studente (mauro, alberto) ←

interessa (alberto, matematica) ←

promuove (mauro, x) ← studente (x, mauro),

ama (x, matematica)

← promuove (mauro, alberto)

Le prime due sono i fatti, la terza è una regola e l’ultima è il goal che si vuole dedurre. Essa è in pratica la negazione della conclusione che si vuole dedurre.

Le istruzioni di un programma in prolog sono clausole di Horn con variabili. Un programma in prolog non indica, quindi, le istruzioni da eseguire algoritmicamente; piuttosto descrive logicamente un insieme di fatti e di regole che costituiscono la base di conoscenza disponibile. Si tratta di un database relazionale che può essere interrogato in vari modi per sapere se una certa relazione è soddisfatta oppure per stabilire come lo possa essere. Il prolog è, quindi, una sorta di dimostratore automatico di teoremi perché stabilisce cosa è deducibile dalla base di conoscenza posseduta. Esso tuttavia sviluppa calcoli logici nella loro generalità e astrazione, seguendo gli schemi prima introdotti, ma senza problemi di efficienza e rapidità; esistono linguaggi tipo-prolog che, pur seguendone la traccia, si pongono problemi di snellimento e di abbreviazione dei calcoli e, per questo, introducono alcuni artifici che difficilmente possono essere descritti in termini logici. Resta comunque il loro basarsi su una impostazione non imperativa (istruzioni da eseguire), ma descrittiva (stato dei fatti da descrivere compiutamente).