punteggiato
punteggiato
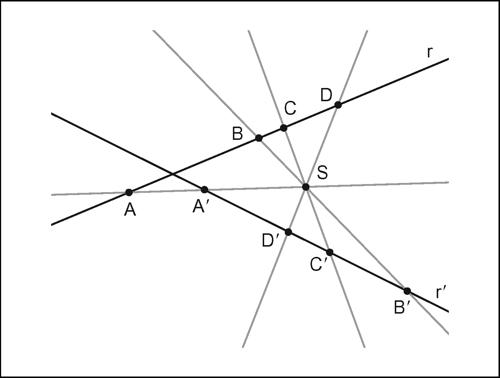
punteggiato nel piano o nello spazio tridimensionale proiettivo, ogni sottoinsieme pensato come insieme di punti. Per esempio, nel piano una retta punteggiata (detta anche semplicemente punteggiata) è una retta pensata come insieme di punti (e la retta è il sostegno di tale forma geometrica); nello spazio tridimensionale si considerano analogamente piani punteggiati e l’intero spazio come spazio punteggiato. L’aggettivazione ha due motivi: il primo motivo consiste nel fatto che alcuni elementi possono essere pensati anche in altro modo: per esempio il piano si può considerare come un fascio di rette, e in tal caso è detto piano rigato, e lo spazio può pensarsi come una stella di piani, e in tal caso è detto spazio di piani. Il secondo motivo consiste nel fatto che alcuni elementi possono essere visti come l’uno la proiezione dell’altro o, come anche si dice, tra loro proiettivi. Per esempio, nello spazio proiettivo tridimensionale una stella di rette proietta su qualunque retta dello spazio che non passi per il centro della stella una retta punteggiata, e viceversa; analogamente, una stella di piani proietta su un qualunque piano che non passi per il centro della stella un piano rigato, e viceversa. Nel piano proiettivo, analogamente, sono tra loro proiettivi una retta punteggiata e un fascio di rette (il cui centro non appartenga alla retta); due rette punteggiate, proiettate dallo stesso fascio, sono allora tra loro proiettive, nel senso che se A, B, C, D sono quattro punti della prima punteggiata e A′, B′, C′, D′ sono i loro punti corrispondenti in tale proiezione allora i birapporti (ABCD) e (A′B′C′D′ ) sono uguali.