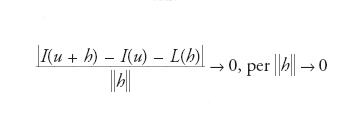punti stazionari
di Daniele Cassani -
Enciclopedia della Scienza e della Tecnica (2008)
punti stazionari
Si consideri un funzionale, ovvero un’applicazione I:E→ℝ, definita su uno spazio normato E. Si ha che I è (Fréchet-) differenziabile in u∈E se esiste un’applicazione lineare L:E→ℝ tale che
e scriviamo L=I′(u), per denotare il differenziale (di Fréchet) del funzionale I nel punto u∈E (si osservi che il differenziale di un applicazione lineare è l’applicazione stessa). Se la condizione precedente vale per ogni u∈E, I si dice differenziabile su E e sono detti punti stazionari o critici per I i punti u∈E soluzioni dell’equazione: I′(u)=0.