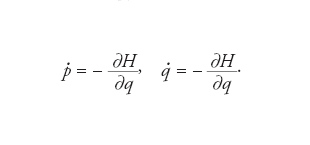punto omoclino

punto omoclino

Un punto (x∙₀,x∙₀) ∈ℝⁿ×ℝⁿ nello spazio delle fasi di un sistema dinamico con n gradi di libertà x∙=f(x) tale che la soluzione (orbita) passante per esso si avvicini asintoticamente per t→±∞ a un punto di equilibrio p. Un’orbita passante per un punto omoclino è a sua volta detta omoclina. In altri termini, indicando con W^s(p) e W^u(p) rispettivamente gli insiemi dei punti che si avvicinano a p quando t→+∞ e t→−∞, i punti omoclini sono per definizione gli elementi dell’insieme W⁰(p)=W^s(p)∩W^u(p). Si parla di punto eteroclino quando per t→+∞ e t→−∞ l’orbita tende a punti di equilibrio distinti. La nozione di punto omoclino è estremamente importante nello studio delle proprietà strutturali dei sistemi dinamici e può essere generalizzata in varie direzioni. Per es., essa ha evidentemente senso anche nel caso di sistemi a tempo discreto. Nel caso di sistemi hamiltoniani con n gradi di libertà

Si dice omoclino un punto (p₀,q₀)∈ℝⁿ×ℝⁿ nel dominio di definizione della funzione di Hamilton H=H(p,q) tale che la soluzione (traiettoria) passante per esso si avvicini asintoticamente per t→±∞ a un toro k-dimensionale T_k, con 0〈k〈n. Per es., un toro unidimensionale T₁ si riduce a una soluzione periodica (traiettoria chiusa), mentre per k=2 otteniamo la familiare figura a forma di ciambella. L’individuazione di soluzioni omocline di un sistema hamiltoniano con hamiltoniana H=H(p,q) arbitraria è in generale estremamente difficile. Tuttavia, se è possibile scegliere coordinate canoniche (p′,q′) tali che H=H₀(p′)+εH₁(p′,q′) con ε>0 ‘piccolo’ e H₁(p′,q′)=H₁(p′,q′+2π), allora le soluzioni omocline possono essere espresse in termini di una serie di potenze in ε. Osserviamo che la semplice esistenza di soluzioni omocline (senza dunque l’indicazio­ne esplicitata di una procedura per la loro costruzione) può essere provata sotto condizioni molto più generali.

→ Sistemi dinamici. Origini e sviluppo