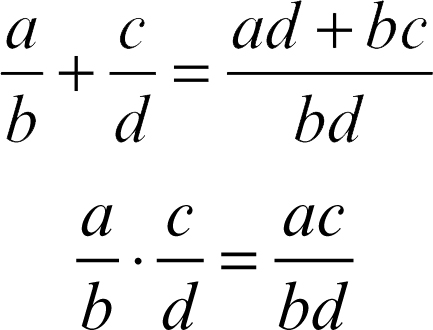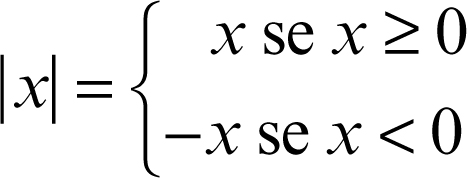Q
Q
Q (insieme dei numeri razionali) insieme numerico, indicato con il simbolo Q (da «quoziente») che estende l’anello Z dei numeri interi. Se a e b sono numeri interi, con b ≠ 0, non sempre è definito in Z il risultato della divisione a : b e dunque, fin dall’antichità, e ben prima che fosse inventata la notazione decimale con la virgola, furono estesi i numeri interi considerando le frazioni. Poiché le frazioni esprimono un rapporto, ci sono infinite frazioni che descrivono lo stesso rapporto: per esempio 1/2 = 2/4 = 3/6, ... Frazioni di questo tipo sono dette frazioni equivalenti e, riferite alla stessa unità, rappresentano la stessa quantità. Per tale motivo, si costruisce l’insieme Q a partire dall’insieme Z in modo che ogni numero razionale risulti una classe di frazioni equivalenti.
Formalmente, la costruzione avviene in questo modo: indicato con Z0 l’insieme dei numeri interi diversi da 0 (Z0 = Z{0}), si introduce sul prodotto cartesiano Z × Z0 la relazione di equivalenza ∼, definita come segue: (a, b) ∼ (c, d) se e solo se ad = bc, dove a, c appartengono a Z e b, d appartengono a Z0. Si definisce dunque l’insieme Q come l’insieme quoziente rispetto a tale relazione di equivalenza. In simboli:
Un generico elemento di Q, detto numero razionale, è perciò una classe di equivalenza [(a, b)] di coppie di numeri interi (il secondo dei quali diverso da 0). Convenzionalmente, si indica la classe [(a, b)] mediante la notazione frazionaria
Le due operazioni di addizione (denotata con il simbolo +) e moltiplicazione (denotata con i simboli × o ⋅, che tuttavia spesso sono omessi) sono definite in Q come segue
Tali operazioni sono in effetti ben definite, nel senso che non dipendono dal particolare rappresentante considerato nella classe di equivalenza. Entrambe godono della proprietà associativa e commutativa; la moltiplicazione gode della proprietà distributiva rispetto all’addizione ed entrambe ammettono elemento neutro: 0 = 0/1 è elemento neutro dell’addizione, mentre 1 = 1/1 è elemento neutro della moltiplicazione. Ogni elemento a /b è invertibile rispetto all’addizione, con inverso −a /b, detto opposto di a /b (in effetti vale −a /b = (−a)/b = a /(−b)); ogni elemento a /b con a ≠ 0 è invertibile rispetto alla moltiplicazione, con inverso b /a che è detto il reciproco di a /b ed è anche indicato con il simbolo (a /b)−1.
Pertanto, dotato di tali operazioni, Q acquisisce la struttura algebrica di campo diversamente dall’insieme Z dei numeri interi dotato delle operazioni di addizione + e moltiplicazione ⋅ che non è un campo, ma solamente un anello perché nessun elemento diverso da 1 e −1 ammette inverso rispetto alla moltiplicazione.
L’insieme Z dei numeri interi si immerge in Q tramite l’omomorfismo iniettivo di anelli i: Z → Q definito da i (n) = n /1; tale → immersione permette in effetti di identificare Z con il sottoinsieme di Q costituito da tali numeri; per questo, nell’ambito dei numeri razionali si scrive n al posto di n /1. Ogni numero intero n non nullo possiede un inverso moltiplicativo in Q, che coincide con n−1 = 1/n. Segue che, comunque dati due numeri interi a e b (con b ≠ 0), è definito in Q il risultato della divisione a : b, vale a dire il loro rapporto (o frazione), a cui corrisponde il numero razionale a /b = ab−1 = a ⋅ 1/b; viceversa ogni numero razionale può essere per costruzione scritto in questo modo. Dunque ogni equazione a coefficienti interi del tipo ax + b = 0, con a ≠ 0, possiede soluzione −b /a; viceversa Q coincide con l’insieme di tali soluzioni. Tutto ciò esprime il fatto che Q è il campo dei quozienti di Z, vale a dire è il più piccolo campo contenente Z (a meno di isomorfismo).
Un numero razionale a /b è detto positivo (rispettivamente negativo) se è positivo (rispettivamente negativo) il numero intero ab; si scrive allora a /b > 0 (rispettivamente a /b < 0). Similmente, un numero razionale a /b è detto non negativo (rispettivamente non positivo) se è non negativo (rispettivamente non positivo) il numero intero ab; si scrive allora a /b ≥ 0 (rispettivamente a /b ≤ 0). A partire da tale nozione è possibile introdurre su Q un ordinamento totale (sempre indicato con il simbolo ≤) che estende quello definito in Z e definito come segue:
Se x e y sono due numeri razionali, si scrive allora x < y (o equivalentemente y > x) se y − x > 0; la relazione < è l’ordinamento stretto associato all’ordinamento ≤. L’ordinamento ≤ è compatibile con la struttura di campo e soddisfa l’assioma di → Archimede; determina pertanto su Q una struttura di campo archimedeo. Inoltre, tale ordinamento è denso, nel senso che, per ogni coppia di numeri razionali x e y, con x < y, esiste un terzo numero razionale z tale che x < z < y. Tale ordinamento non è però continuo, vale a dire non soddisfa l’assioma di → Dedekind.
Se x è un numero razionale, si definisce allora il suo modulo (o valore assoluto)
Il modulo definisce una distanza d su Q, indicata da d(x, y) = |x − y|; dotato di tale distanza, Q acquisisce la struttura di spazio metrico. Come spazio metrico Q non è completo (→ completezza): per esempio, si può dimostrare che la successione di numeri razionali (1 + 1/n)n non ammette limite in Q (in effetti essa converge al numero di Nepero e, che è un numero irrazionale). La non completezza di Q come spazio metrico con la distanza indotta dal modulo è equivalente alla non continuità dell’ordinamento ≤. Questi fatti inducono a cercare un ampliamento di Q che sia allo stesso tempo un campo completo e un campo archimedeo continuo: tale è l’insieme R dei numeri reali, che coincide con il completamento metrico di Q.