quadrato latino
quadrato latino
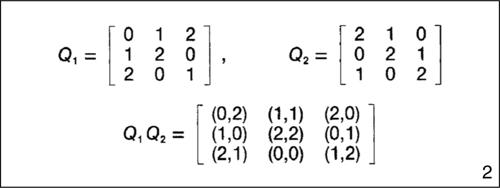
quadrato latino matrice quadrata di ordine n avente per elementi n2 numeri o simboli in modo tale che nessuno di essi compaia due volte nella stessa riga o nella stessa colonna. La → tavola pitagorica che descrive l’operazione di un gruppo finito è un quadrato latino. Prodotto di due quadrati latini Q1 e Q2 dello stesso ordine è la matrice di ordine n avente per elemento di posto (i, j) la coppia ordinata dei numeri che occupano lo stesso posto in Q1 e in Q2; Q1 e Q2 si dicono ortogonali se il loro prodotto contiene solo coppie distinte. Se due quadrati, dello stesso ordine, sono formati con sistemi di simboli differenti, tale quadrato prodotto è detto quadrato greco-latino perché si utilizzano lettere dell’alfabeto latino e greco per distinguere i termini della stessa coppia. Un insieme di k quadrati latini dello stesso ordine si dice ortogonale se essi sono a due a due ortogonali, e k si dice dimensione dell’insieme. La dimensione massima che può avere un insieme ortogonale di quadrati latini di ordine n è n − 1. Eulero, che descrisse tali quadrati nell’articolo Recherches sur une nouvelle espece de quarres magiques (Ricerche su un nuovo tipo di quadrati magici) del 1782 congetturò che non esistesse alcun quadrato greco-latino di ordine 2n per n dispari maggiore di 1 e, in particolare, avanzò l’ipotesi che non si potesse risolvere il seguente problema noto come problema dei 36 ufficiali di Eulero: disporre su una scacchiera quadrata con 36 caselle 36 ufficiali di 6 reggimenti diversi e con 6 gradi diversi in modo che in ogni riga e colonna ci siano tutti i gradi e tutti i reggimenti. Soltanto nel 1901 il matematico francese G. Tarry dimostrò che in effetti il problema è insolubile e nel 1960 è stato dimostrato, con l’ausilio di un computer, che esistono quadrati greco-latini di ogni ordine salvo 2 e 6. I quadrati latini sono utilizzati per la progettazione di esperimenti (in modo da variare in tutti i modi possibili i fattori sottoposti ad analisi statistica), in teoria dell’informazione, per lo studio dei codici correttori di errori e nello studio dei piani proiettivi finiti (→ geometria finita); l’analisi delle loro proprietà è oggetto di studio dell’analisi combinatoria.