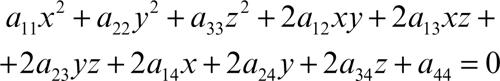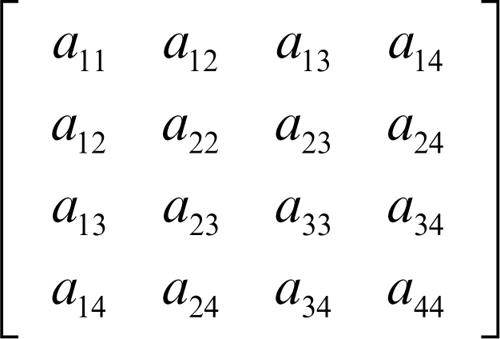quadrica

quadrica

quadrica superficie algebrica del secondo ordine ottenuta come luogo dei punti le cui coordinate soddisfano un’equazione di secondo grado del tipo:

La matrice quadrata simmetrica del quarto ordine A = (a_ij) (con i, j = 1, ..., 4 e a_ij = a_ji)

è detta matrice della quadrica e il suo determinante è detto discriminante della quadrica. Se det(A) ≠ 0, si ha una quadrica non degenere o irriducibile o generale e tutti i suoi punti sono punti semplici. Inoltre una quadrica è detta rigata se contiene due sistemi di rette, detti schiere, tali che per ciascun punto della quadrica passi una e una sola retta di ciascuna schiera.

Classificazione proiettiva delle quadriche

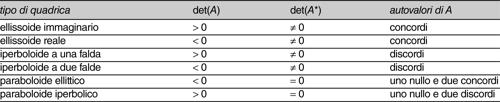
Dal punto di vista proiettivo le proprietà di una quadrica, supposta a punti reali, dipendono dalla matrice A: se il suo determinante è minore di zero (det(A) < 0) allora i punti sono tutti ellittici, se è maggiore di zero (det(A) > 0) sono tutti iperbolici. Ogni punto di una quadrica non degenere si trova su due rette distinte che costituiscono l’intersezione della quadrica con il piano tangente in quel punto; tali rette sono reali se il punto è iperbolico, complesse coniugate se il punto è ellittico. Nel caso di quadrica degenere, si considera la caratteristica della matrice A:

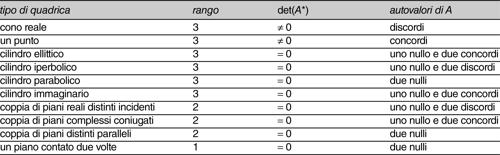
• se è uguale a 3, la quadrica risulta essere un cono con il vertice nel punto doppio, l’unico di questo tipo della quadrica essendo tutti gli altri punti parabolici;

• se la caratteristica di A è 2, la quadrica risulta essere formata da due piani distinti e ha come punti doppi quelli della retta a essi comune;

• se A ha caratteristica 1, la quadrica risulta essere un piano doppio (cioè considerato due volte).

Una quadrica non degenere determina nello spazio proiettivo una → polarità, ossia una corrispondenza biunivoca involutoria in cui due punti P e P′ si corrispondono quando separano armonicamente (→ birapporto) i punti intersezione della quadrica con la retta per P e P′. I punti corrispondenti (→ punti coniugati) di un punto P sono situati su un piano (piano polare); si stabilisce così una corrispondenza biunivoca tra punti e piani (polarità) che associa a ogni punto P il piano π luogo dei punti coniugati di P e viceversa a ogni piano π un punto P (polo) che ha per piano polare π.

Classificazione affine delle quadriche

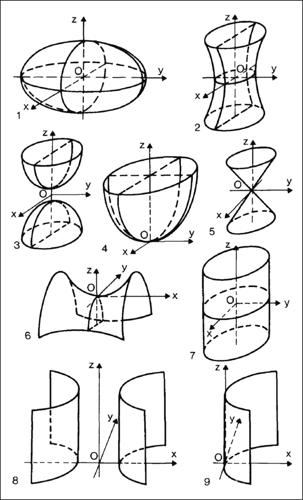
Dal punto di vista affine, la classificazione si effettua considerando la conica intersezione con il piano improprio. Se tale conica è non degenere e immaginaria, la quadrica è un ellissoide, se è non degenere e reale è un iperboloide (a una falda se det(A) > 0, a due falde se det(A) < 0), mentre se la conica è degenere la quadrica è un paraboloide (iperbolico se det(A) > 0, ellittico se det(A) < 0). La sfera è un particolare ellissoide la cui conica all’infinito prende il nome di cerchio assoluto. Una quadrica degenere per la quale la conica all’infinito non è degenere è un cono; se invece la conica all’infinito è degenere, si ha un cilindro (iperbolico, parabolico o ellittico secondo che essa si spezzi in due rette reali distinte, o reali coincidenti o immaginarie coniugate). Centro di una quadrica è il polo del piano all’infinito: esso è proprio nelle quadriche a centro (l’iperboloide e l’ellissoide), è improprio nel caso del paraboloide; nel cono e nel cilindro (che è un cono con vertice improprio) il centro coincide con il vertice. I piani polari dei punti impropri si chiamano piani diametrali e le loro intersezioni a due a due si chiamano diametri della quadrica.

Proprietà metriche di una quadrica

Sotto l’aspetto metrico ha importanza il caso in cui un diametro è perpendicolare al piano polare del suo punto improprio, nel qual caso il diametro è detto asse e il piano è detto piano principale; vertice della quadrica è un punto intersezione con un suo asse. Nelle quadriche a centro si hanno tre piani principali a due a due ortogonali, nei paraboloidi si hanno due piani principali tra loro ortogonali. Se la quadrica è rotonda, cioè è ottenuta facendo ruotare una conica attorno a uno dei suoi assi, ogni piano per l’asse di rotazione è principale.

Altra classificazione

Una classificazione completa delle quadriche si può sintetizzare tenendo conto anche del rango della matrice A, del segno degli autovalori di A, del determinante della matrice A*, ottenuta da A eliminando la quarta riga e la quarta colonna (cioè considerando soltanto i coefficienti di secondo grado). Si ottengono così sei tipi di quadriche non degeneri e dieci tipi di quadriche degeneri, come schematizzato nelle tabelle che seguono.

Quadriche in un riferimento cartesiano

Scelto opportunamente il sistema di riferimento, l’equazione di una quadrica assume una forma più semplice, detta forma canonica. Si riportano le equazioni canoniche di alcune quadriche reali non degeneri: