quaterna armonica

quaterna armonica

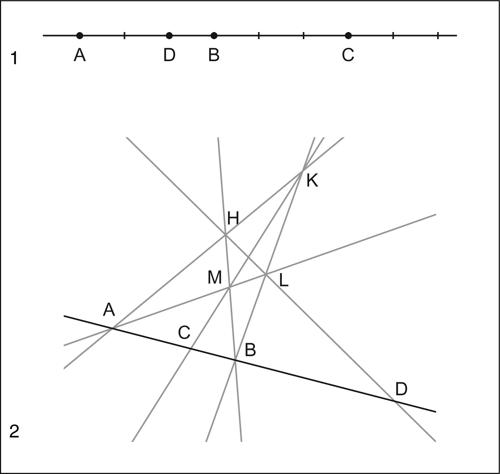
quaterna armonica o gruppo armonico, insieme di quattro punti A, B, C, D allineati su una retta orientata tali che il loro birapporto valga −1; in simboli (A, B, C, D) = −1. I punti C e D dividono armonicamente i punti A e B, nel senso che dividono il segmento AB, esternamente e internamente, nello stesso rapporto. Reciprocamente anche i punti A e B dividono armonicamente i punti C e D, in virtù della proprietà del birapporto che stabilisce che (A, B, C, D) = (C, D, A, B). I punti di una quaterna armonica si dicono anche punti armonici e conservano tale proprietà in una qualsiasi trasformazione proiettiva (e perciò uno di essi può anche essere un punto all’infinito). Per costruire una quaterna armonica si possono considerare quattro punti H, K, L, M a tre a tre non allineati e considerare tutte le sei rette che li congiungono a due a due (tale configurazione è detta quadrangolo completo). Si considerano quindi il punto A = HK ∩ LM e il punto B = HM ∩ KL e si traccia la retta per A e B. Si indicano con C il punto in cui la retta AB interseca KM e con D il punto in cui AB interseca HL. La quaterna A, B, C, D è una quaterna armonica.