quattro colori, problema dei

quattro colori, problema dei

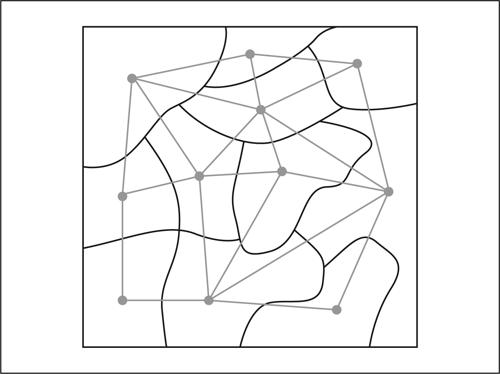
quattro colori, problema dei problema classico, nato dalla cartografia e risolto positivamente solo negli anni Settanta del secolo scorso. Il problema nasce da una domanda semplice: qual è il numero minimo di colori necessario e sufficiente per rappresentare su una carta gli stati confinanti (che dovranno figurarvi di colore diverso)? Da un punto di vista matematico gli stati sono regioni del piano connesse, e due stati si dicono confinanti se hanno una linea di confine in comune (non soltanto un numero finito di punti). Il problema rimane sostanzialmente inalterato se le regioni si trovano, anziché su di un piano, sulla superficie di una sfera (la Terra): in quest’ultimo caso, basta scegliere un punto P interno a una regione e proiettare la superficie sul piano tangente nel punto diametralmente opposto a P; ci si riporta così al caso di regioni piane. Il problema fu storicamente formulato nel 1853 da uno studente inglese, Francis Guthrie, al fratello Frederick, studente di matematica che aveva A. De Morgan come uno dei suoi insegnanti. Guthrie formulò la congettura che fossero sufficienti quattro colori. Si può dimostrare facilmente che tre colori sono insufficienti a colorare una mappa, mentre ne sono sufficienti al più cinque; l’ipotesi che quattro colori siano sufficienti ha trovato una dimostrazione rigorosa soltanto in anni relativamente recenti. Il problema è formalizzabile attraverso la definizione della relazione «essere confinanti» nell’insieme degli stati rappresentati sulla mappa; tale relazione è equivalente ad «avere colori diversi nella rappresentazione». Si può quindi schematizzare il problema con un grafo: gli elementi dell’insieme sono gli stati e ciascuno di essi è un nodo del grafo, mentre ogni arco indica un cambiamento di colore. Le idee guida per una dimostrazione furono date nel 1879 da Alfred Kempe, un avvocato londinese appassionato di matematica, e da P.J. Heawood, ma solo nel 1976 con l’aiuto di un potente computer (e 1200 ore macchina) e attraverso un sistema di lettura di tutte le possibilità sul grafo che rappresenta il problema, i matematici K. Appel e W. Haken giunsero a una risoluzione algoritmica che può essere considerata come una dimostrazione (nel cosiddetto teorema dei quattro colori), certamente non di tipo classico, bensì ottenuta attraverso la mole di possibilità esplorate dall’elaboratore e con una procedura algoritmica che dimostra un’ottima stabilità. Gli sforzi per la risoluzione del problema hanno dato tra l’altro un importante contributo allo sviluppo della teoria dei grafi e alla topologia.