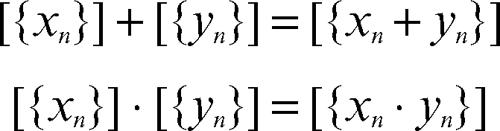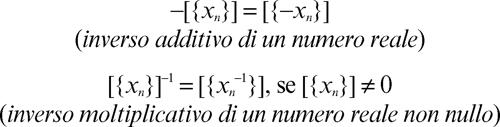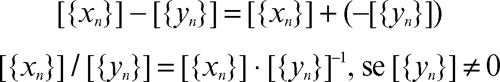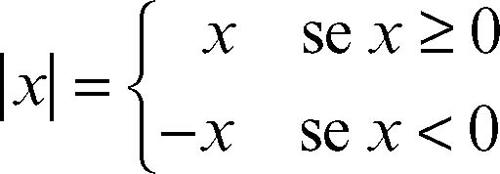R
R
R (insieme dei numeri reali) insieme numerico, denotato con il simbolo R, che comprende tutti i numeri che è possibile scrivere in forma decimale, con parte decimale finita, infinita periodica o infinita non periodica. Formalmente, R è definito come il completamento metrico dell’insieme Q dei numeri razionali; include cioè, oltre ai numeri razionali, tutti i limiti di tutte le successioni convergenti di numeri razionali.
L’insieme R dei numeri reali può essere rappresentato su una retta, fissando su di essa un punto origine O (cui corrisponde il numero 0) e un segmento unitario OU (in modo tale che al punto unitario U corrisponda il numero 1); così facendo, si stabilisce una corrispondenza biunivoca tra l’insieme R e l’insieme dei punti della retta, che acquisisce così una caratteristica di completezza, assicurata dall’assioma di → Dedekind. Se invece sulla retta si rappresentano i soli numeri razionali, questi pur essendo densi (tra due distinti numeri razionali ne esiste sempre uno compreso tra essi e diverso da entrambi), non la completano, poiché infiniti punti della retta non sono rappresentanti di alcun numero razionale. Per esempio, se si costruisce un quadrato sul segmento unitario OU e si riporta con il compasso centrato in O la sua diagonale sulla retta, nel verso positivo, si ottiene il punto P rappresentante di √(2). Ma non esiste alcun numero razionale positivo il cui quadrato sia uguale a 2; quindi la retta razionale (formata cioè solo da punti rappresentanti di numeri razionali) risulta priva del punto P in corrispondenza del quale ha un “buco” che ne interrompe la continuità.
Il procedimento di costruzione dell’insieme R a partire da Q consiste sostanzialmente nel “riempire” tali buchi; si tratta di un procedimento di tipo astratto, così da dare un significato matematico-formale alla parola intuitiva “buco” rimanendo nell’ambito dei numeri razionali.
La necessità di andare oltre ai numeri razionali
Fin dall’antichità si era scoperto che non erano sufficienti le frazioni (e quindi i numeri razionali) per descrivere tutti i rapporti tra grandezze e che vi sono grandezze tra loro incommensurabili (→ commensurabilità); si deve infatti già alla scuola pitagorica la scoperta che il rapporto tra la diagonale e il lato di un quadrato, cioè √(2), non è esprimibile con una frazione (→ pitagorismo). Procedimenti ingegnosi furono anche escogitati per un altro rapporto importante, per il quale non si trovava una frazione che lo esprimesse esattamente: il rapporto tra la circonferenza e il suo diametro, vale a dire π. Per il suo calcolo, Archimede di Siracusa, già nel iii sec. a.C., inventò una procedura che anticipa i moderni metodi infinitesimali (→ Archimede, metodo di (per pi greco)), ma dovettero passare molti secoli prima che si avvertisse l’esigenza di comprendere la natura di questi “strani” numeri non esprimibili come frazioni. In particolare, lo studio delle equazioni, che poté fare progressi significativi soltanto con l’affermarsi di un simbolismo algebrico adeguato, condusse, tra il xviii e il xix secolo a una prima differenziazione di tali numeri, quella tra → numeri algebrici, soluzioni di equazioni algebriche a coefficienti interi, e → numeri trascendenti, di cui fu dimostrata l’esistenza nel 1844 da J. Liouville.
Soltanto alla fine del xix secolo, dopo lo sviluppo impetuoso dell’analisi e il processo di sistemazione avviato da A.-L. Cauchy, si avvertì la necessità di costruire rigorosamente il campo dei numeri reali a partire da quello dei numeri razionali, portando così a compimento quel processo di aritmetizzazione dell’analisi che aveva caratterizzato il secolo (→ matematica).
La costruzione di R a partire da Q
Esistono due possibili costruzioni dell’insieme R dei numeri reali a partire dai numeri razionali; esse furono proposte entrambe nel 1872 rispettivamente dai matematici tedeschi G. Cantor e R. Dedekind. Mentre la costruzione di Cantor coglie come caratterizzanti le proprietà metriche di Q e presenta R quale completamento di Q, inteso come spazio metrico, quella di Dedekind si fonda sulle proprietà dell’ordinamento definito tra numeri razionali e presenta R quale completamento di Q, inteso come insieme ordinato. Il risultato delle due costruzioni è comunque equivalente e qui, seguendo Cantor, i numeri reali saranno definiti mediante le successioni di Cauchy. Per la definizione dei numeri reali secondo Dedekind, si veda invece → Dedekind, sezione di.
La costruzione di R e la definizione di numero reale dovute a Cantor
Cantor costruisce i numeri reali a partire dalle successioni di → Cauchy. Mentre ogni successione {xn} di numeri razionali convergente a un numero razionale soddisfa la condizione di Cauchy, è cioè tale che (qualunque siano gli indici m e n):
il viceversa non è vero: esistono cioè successioni di Cauchy, i cui termini sono numeri razionali, che non convergono a un numero razionale e tale è per esempio il caso della successione (1 + 1/n)n che converge al numero e (→ e, numero di Nepero). In tali successioni i termini si accumulano sempre più intorno a un “valore”, che però non esiste come numero razionale: tale valore mancante è un “buco” che occorre colmare. Equivalentemente, come spazio metrico dotato della distanza indotta dal modulo, Q non è completo: R costituisce il completamento metrico di Q, vale a dire esso è, a meno di isometrie, il più piccolo spazio metrico contenente una copia di Q in cui ogni successione di Cauchy converge.
Più precisamente, indicato con Γ l’insieme delle successioni di Cauchy i cui termini sono numeri razionali, si considera su Γ la seguente relazione d’equivalenza tra successioni:
Due successioni sono quindi equivalenti se e solo se la loro differenza converge a 0.
Come insieme, R è definito come l’insieme quoziente Γ/~:
dove [{xn}] indica la classe di equivalenza della successione di Cauchy {xn}. Un numero reale è dunque una classe di equivalenza di successioni di numeri razionali che soddisfano la condizione di Cauchy.
Le operazioni in R
Se {xn} e {yn} sono due successioni di Cauchy, allora anche le successioni {xn + yn} e {xn ⋅ yn} soddisfano la condizione di Cauchy e ciò permette di definire in R le due operazioni + e ⋅, dette rispettivamente addizione e moltiplicazione, come segue:
Tali operazioni risultano essere ben definite, vale a dire che esse non dipendono dalla scelta dei rappresentanti delle due classi. Dotato di queste due operazioni, l’insieme dei numeri reali R acquisisce la struttura di campo: (R, +, ⋅) è un campo. Le due operazioni sono infatti associative e commutative, sono legate dalla proprietà distributiva e ammettono elemento neutro: l’elemento neutro dell’addizione è la classe di equivalenza delle successioni convergenti a 0 (indicata per semplicità con il simbolo 0), mentre l’elemento neutro della moltiplicazione è la classe di equivalenza delle successioni convergenti a 1 (indicata per semplicità con il simbolo 1). Ogni elemento (rispettivamente, ogni elemento non nullo) di R risulta essere invertibile rispetto all’addizione (rispettivamente, rispetto alla moltiplicazione). Più in particolare vale:
dove nella definizione dell’inverso moltiplicativo vanno invertiti solamente i termini non nulli della successione {xn} e la condizione [{xn}] ≠ 0 assicura che i termini nulli sono al più in numero finito.
Se [{xn}] è un numero reale, allora il numero reale −[{xn}] = [{−xn}] è detto l’opposto di [{xn}]. Se [{xn}] è un numero reale ≠ 0, allora il numero reale [{xn}]−1 = [{xn−1}] è detto il reciproco di [{xn}]. A partire dalle due operazioni di addizione e moltiplicazione si definiscono le operazioni inverse di sottrazione e divisione, definite rispettivamente da
Q è sottocampo di R
L’insieme Q dei numeri razionali si immerge in R, mediante l’applicazione che associa a un numero razionale q la classe di equivalenza della successione che vale costantemente q. Mediante tale applicazione, Q risulta naturalmente identificato con l’insieme delle classi di equivalenza delle successioni di numeri razionali convergenti a un numero razionale: tale insieme è chiuso rispetto alle operazioni di addizione e moltiplicazione definite tra classi di successioni; viceversa, ristrette a tale insieme, tali operazioni coincidono con le analoghe operazioni definite in Q. Pertanto, Q è un campo isomorfo a un sottocampo di R e, per semplicità, è direttamente considerato come un sottocampo di R.
R è un campo ordinato
L’ordinamento ≤ di cui è dotato Q si estende in modo naturale all’insieme dei numeri reali: se x = [{xn}] e y = [{yn}] sono due numeri reali, allora si pone x ≤ y (e si dice che x è minore o uguale di y) se x = y oppure se esiste un numero naturale n0 tale che, per ogni n ≥ n0, vale xn ≤ yn, vale a dire se la successione {xn} è definitivamente minore o uguale della successione {yn}. Tale ordinamento è ben definito ed è totale, nel senso che comunque presi due numeri reali x e y, allora vale necessariamente x ≤ y oppure y ≤ x. Se x e y sono due numeri reali con x ≤ y e x ≠ y, si scrive allora x < y e si dice che x è minore di y (o equivalentemente si scrive y > x e si dice che y è maggiore di x): ci si riferisce a esso come all’ordinamento stretto associato alla relazione d’ordine ≤. Un numero reale x è detto positivo (rispettivamente negativo) se x > 0 (rispettivamente x < 0). Come nel caso dei numeri razionali, l’ordinamento ≤ è compatibile con la struttura di campo di cui è dotato R, nel senso che valgono i due seguenti assiomi, dove x e y indicano due arbitrari numeri reali:
• se x ≤ y, allora ∀z ∈ R, x + z ≤ y + z
(compatibilità con l’addizione)
• se 0 ≤ x e 0 ≤ y, allora 0 ≤ x ⋅ y
(compatibilità con la moltiplicazione).
Dotato dell’ordinamento ≤, il campo R acquisisce la struttura di campo ordinato.
R è uno spazio metrico completo
Se x è un numero reale, si definisce il suo modulo (o valore assoluto), indicato con |x|) nel seguente modo:
Il modulo individua una distanza su R, definita da d(x, y) = |x − y|; dotato di tale distanza, R acquisisce la struttura di spazio metrico, rispetto alla quale Q è un sottospazio metrico: la distanza definita su Q coincide con la distanza indotta su di esso a partire dal modulo di un numero reale. Per sua stessa definizione, R, dotato di tale distanza, è uno spazio metrico completo: ogni successione di Cauchy i cui termini sono numeri razionali o più in generale reali converge a un numero reale. Per costruzione, inoltre, ogni numero reale è limite di una successione di numeri razionali; da ciò segue che, a meno di isometrie, R è il minimo campo completo contenente Q, vale a dire R è il completamento metrico di Q. Il fatto che ogni numero reale è limite di una successione di numeri razionali si esprime dicendo che Q è denso in R; ciò vuol dire che, per ogni numero reale, esistono numeri razionali arbitrariamente vicini a esso:
Ogni numero reale x può essere espresso mediante una → frazione continua: ciò equivale a dare una particolare successione di numeri razionali convergente a x (la successione delle ridotte della frazione continua); tale successione fornisce le “migliori” approssimazioni mediante numeri razionali di x.
R ha la cardinalità del continuo
Un numero reale non razionale è detto irrazionale. Un numero reale α è detto algebrico se esiste un polinomio p(x), a coefficienti nel campo Q dei numeri razionali, che si annulla in α; il minimo grado di un tale polinomio è detto grado di α. Ogni numero razionale q è algebrico, in quanto annulla il polinomio x − q: i numeri razionali coincidono con i numeri algebrici di grado 1. Ogni numero algebrico di grado maggiore di 1 è irrazionale, ma non vale il viceversa: un numero irrazionale non algebrico è detto trascendente. Un esempio classico di numero irrazionale algebrico è √(2) giacché annulla il polinomio x 2 − 2. Esempi di numeri trascendenti sono invece π e il numero e. Pur essendo ambedue densi nell’insieme dei numeri reali, i numeri trascendenti sono “molti di più” dei numeri algebrici: l’insieme dei numeri algebrici possiede infatti la cardinalità del numerabile (vale a dire quella dei numeri naturali) e perciò l’insieme dei numeri trascendenti possiede la stessa cardinalità di R, la cardinalità del continuo (→ Cantor, procedimento diagonale di; → continuo, ipotesi del).
R è l’unico campo archimedeo completo
Come nel caso dei numeri razionali, l’ordinamento ≤ definito su R è denso e soddisfa l’assioma di → Archimede. Come campo ordinato, R acquisisce pertanto la struttura di campo archimedeo. Diversamente dal caso dei numeri razionali, l’ordinamento definito sui numeri reali è anche continuo (→ ordinamento). Ciò vuol dire che vale l’assioma di → Dedekind. Il fatto che in R sia soddisfatto l’assioma di Dedekind si esprime dicendo che R è completo come insieme ordinato; la completezza di R come insieme ordinato equivale di fatto alla sua completezza come spazio metrico.
Ogni campo archimedeo si immerge in R; la sua completezza esprime dunque il fatto che R è il più grande campo archimedeo. A meno di isomorfismi d’ordine, esso è l’unico campo archimedeo completo.
Il campo R non è algebricamente chiuso
Ciò vuol dire che esistono polinomi a coefficienti reali privi di radici reali. Questo è per esempio il caso del polinomio p(x) = x 2 + 1: poiché il quadrato di un numero reale è sempre positivo o nullo, segue che p(α) = α2 + 1 ≥ 0 per ogni numero reale α. La ricerca di un campo in cui tale polinomio si possa fattorizzare in polinomi di grado 1 è alla base della costruzione del campo C dei numeri complessi: esso è il minimo campo contenente R insieme a una radice di tale polinomio e coincide con la chiusura algebrica di R.
La retta reale
Come si è già accennato, l’insieme dei numeri reali, in base all’assioma di → Dedekind, può essere messo in corrispondenza biunivoca con i punti di una retta. Dotando la retta di uno dei suoi ordinamenti naturali, è possibile inoltre fare in modo che tale corrispondenza sia un isomorfismo d’ordine, vale a dire che essa preservi le strutture di insiemi ordinati definite rispettivamente su R e sulla retta. Gli assiomi di → Hilbert esprimono allora per la retta delle proprietà analoghe a quelle soddisfatte da R come insieme ordinato, prime fra tutte la completezza e l’archimedeicità. Con retta reale ci si riferisce a una retta dotata di un tale isomorfismo d’ordine.