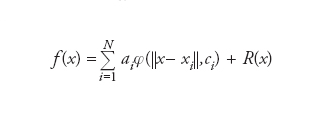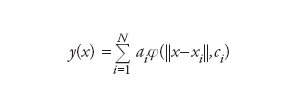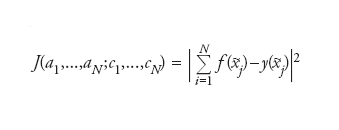radial basis function
radial basis function
Funzione di variabili reali e a valori reali dipendente esclusivamente dalla distanza da un punto fissato, detto centro. Più precisamente, si dice Radial basis function (RBF) una funzione φ:ℝn→ℝ tale che φ(x)=φ(∣∣x-x0∣∣), con x=(x1,...,xn) e ∣∣x∣∣=√____x12+...+xn2. Il simbolo x0 indica il centro. L’importanza delle RBF ha origine nel loro uso per costruire approssimazioni maneggevoli di funzioni reali f qualunque. A tal fine si fissa usualmente una classe di RBF dotata di proprietà interessanti. Scelte comuni sono per es. la gaussiana φ(r,c)=exp(−cr2), r∈ℝ e c>0, (caratterizzata da una rapida decrescita per t→±∞), la funzione multiquadrica φ(r,c)=√__r2+c2 (divergente per r crescenti in valore assoluto) o le cosiddette spline poliarmoniche φ(r,c)=rc per c intero dispari e φ(r,c)=rcln(r) per c intero pari. Esplicitamente, l’espansione di una funzione f in RBF avrà la forma
con i coefficienti ai∈ℝ e ci (nonché i centri xi) da determinarsi in modo da minimizzare l’errore (ovviamente determinato dal resto R(x)) in un senso opportunamente scelto e ottimizzare così la funzione approssimante
Una scelta comune è considerare come misura dell’errore la norma L2 della funzione R(x),
∣∣R(x)∣∣2 = ∫|R(x)|2dx.
Spesso nelle applicazioni la funzione f è nota solo in un insieme finito di punti ∼xj, j=1,...,M, e si è ricondotti al seguente problema non vincolato di ottimizzazione non lineare: dati i valori (∼xj, f(∼xj)), j=1,...,M, determinare ai e ci, i=1,...,N, in modo tale da minimizzare
Questo schema è particolarmente comune nel trattamento delle cosiddette reti neurali a RBF. In questo caso i centri xi indicano le localizzazioni dei neuroni, il processo (iterato più volte) di ottimizzazione modella quello di apprendimento e la funzione f da approssimare è da considerarsi come dato sensoriale. Essa può per es. essere la superficie di un oggetto tridimensionale e in effetti le tecniche precedentemente descritte sono utilizzate per la ricostruzione di immagini in campo medico.