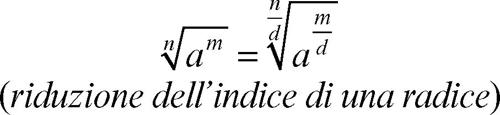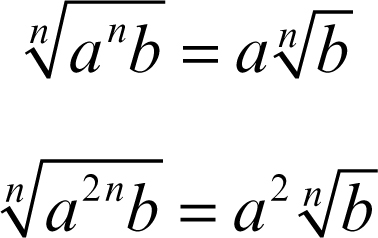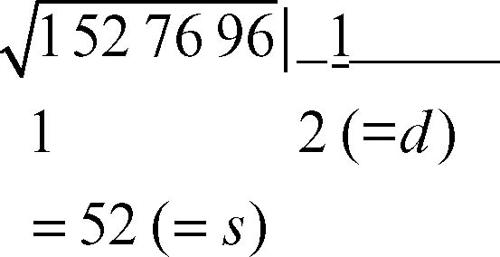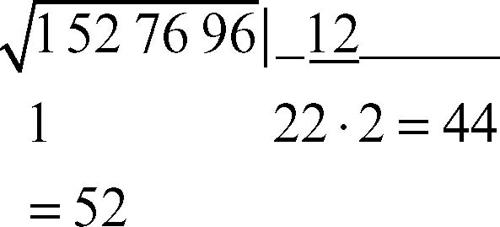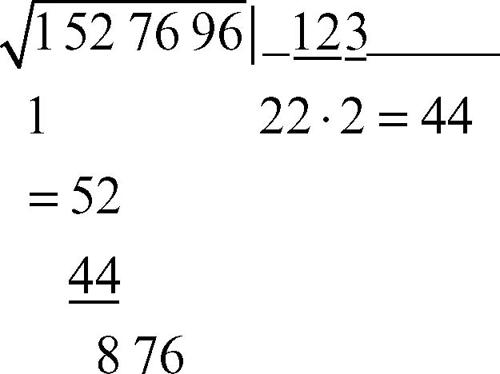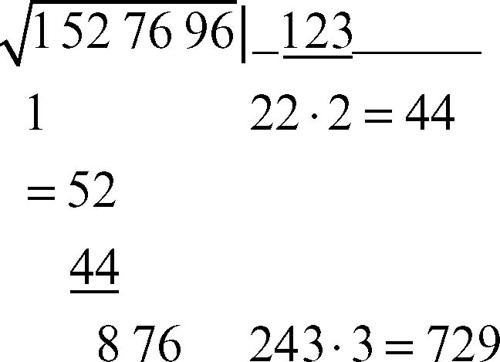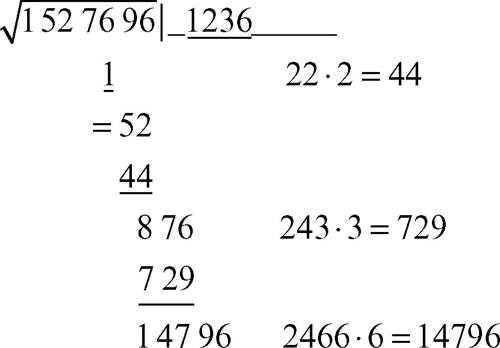radice

radice

radice termine che assume diversi significati a seconda del contesto. In un → albero è il nodo di livello 0 da cui originano i suoi rami. In aritmetica l’estrazione di radice è l’operazione inversa dell’elevazione a potenza che, data la potenza, restituisce la base. In un polinomio è detto radice ognuno dei suoi zeri (cioè dei valori che, sostituiti alle indeterminate, annullano il polinomio) e analogamente sono dette radici le soluzioni di un’equazione. Questi due ultimi significati rimandano comunque all’operazione di estrazione di radice. Proprio dalla distinzione tra la radice vista come risultato di un’operazione inversa dell’elevazione a potenza e la radice vista come soluzione di un’equazione nasce la distinzione tra radice aritmetica e radice algebrica. Nella prima accezione (aritmetica), si può considerare per esempio la radice quarta del numero 81 e scriverla formalmente come

dove il numero 81 e il numero 4 sono detti rispettivamente radicando e indice della radice; il risultato di questa come di qualunque altra operazione deve essere univoco e, quindi, si assume che esso sia +3 perché (+3)⁴ = 81. Nell’accezione algebrica il problema rimanda alla ricerca delle radici dell’equazione algebrica x ⁴ − 81 = 0; il loro insieme è {−3, +3} e tali valori sono le radici algebriche di indice 4 di 81.

Se la scrittura

indica la radice aritmetica del numero a essa fornisce un solo valore x. In particolare, se n è un numero intero dispari, x è l’unico numero reale tale che xⁿ = a; se invece n è un numero intero pari, x è l’unico numero reale positivo, se esiste, tale che xⁿ = a; per questo si scrive, per esempio, √(a²) = |a|.

Alcuni autori danno una definizione più restrittiva ammettendo che la radice possa essere definita soltanto nel caso in cui il risultato dell’elevazione a potenza sia positivo; pertanto la scrittura

è considerata priva di significato. La giustificazione di questa posizione risiede nella possibilità di considerare le radici come potenze con esponente razionale e applicare a esse le relative proprietà (→ potenza). Questa restrizione è necessaria se si vuole poter scrivere, infatti,

perché se non ci si limitasse a radicandi positivi, si avrebbero situazioni contraddittorie, quali la seguente: da un lato

d’altro lato,

oppure ancora

espressione priva di significato in R.

La situazione può essere riassunta come segue.

Radice aritmetica di un numero

Se n è un numero intero positivo (≥ 2) e a è un numero reale non negativo, si chiama radice aritmetica n-esima di a l’unico numero reale non negativo b tale che bⁿ = a; tale numero è indicato con il simbolo

(o anche con a^1/n). Più in particolare, se n = 2 si parla di radice quadrata (e si scrive semplicemente √(a)), se n = 3 si parla di radice cubica, se n > 3 si parla invece di radice quarta, radice quinta, ..., radice n-esima. L’operazione che associa a un numero non negativo la sua radice n-esima va sotto il nome di estrazione di radice (aritmetica) n-esima. Occorre perciò osservare che il simbolo di radice indica sempre la radice aritmetica. Se l’indice n è pari, la radice aritmetica n-esima di un numero reale a è a sua volta un numero reale se e solo se a ≥ 0, altrimenti è un numero complesso. Qualunque sia n intero positivo ≥ 2,

Radice algebrica di un numero

Più in generale si definisce radice algebrica n-esima di un numero reale a un qualsiasi numero reale b che soddisfa una relazione del tipo bⁿ = a, per un opportuno intero positivo n ≥ 2: la nozione di radice algebrica estende quella di radice aritmetica, consentendo che tanto a quanto b possano essere numeri negativi. Qualunque sia n intero positivo ≥ 2, la radice algebrica di 0 è 0

Inoltre:

• se l’indice n è dispari, ogni numero reale a ha una e una sola radice algebrica, dello stesso segno di a. Più precisamente, la radice di un numero a esiste sempre ed è univocamente definita nell’insieme R dei numeri reali. Essa coincide con la radice aritmetica

se a è non negativo, mentre se a è negativo coincide con l’opposto

della radice aritmetica di −a;

• se l’indice n è pari, le radici algebriche di un numero positivo sono due e opposte tra loro, mentre un numero negativo non ha radici algebriche reali. Più precisamente, si ha la seguente dicotomia: se a > 0, allora a possiede due radici algebriche di indice n, vale a dire la sua radice aritmetica

e l’opposta di quest’ultima

se invece a < 0, poiché un numero reale non nullo elevato a una potenza pari produce sempre un risultato positivo, allora a non possiede in R alcuna radice algebrica di indice n. Pertanto, anche non limitandosi a considerare solamente radici aritmetiche, se l’indice n della radice è pari, affinché essa sia definita in R, è necessario assumere che il radicando sia non negativo. Ciò è conseguenza del fatto che il campo R dei numeri reali non è algebricamente chiuso, e in ciò risiede la differenza sostanziale tra il caso reale e quello complesso.

Proprietà delle radici

Valgono le seguenti proprietà delle radici aritmetiche, che si deducono dalle proprietà delle potenze:

Un’ulteriore proprietà (che in effetti è conseguenza di quelle enunciate sopra) è quella che va sotto il nome di proprietà invariantiva:

per ogni intero m > 0. Usando tali proprietà è talvolta possibile ridurre una radice data a una forma più semplice.

Riduzione di una radice

Se il radicando è una potenza il cui esponente possiede fattori comuni con l’indice della radice o non minori di esso, applicando la proprietà invariantiva è possibile ridurre l’indice della radice: se d è il massimo comune divisore di m e n, allora

Se al contrario ogni fattore del radicando è minore dell’indice della radice ed è coprimo con esso, non è possibile effettuare alcuna riduzione di questo tipo e il radicale è pertanto detto irriducibile. Per esempio,

è irriducibile, mentre

non lo è, essendo

Se il radicando è prodotto di due fattori, uno dei quali è una potenza aⁿ, il cui esponente n coincide con l’indice della radice o ne è un suo multiplo, è allora possibile portare fuori dalla radice il termine aⁿ, che diventa così il coefficiente di un radicale. Per esempio:

Viceversa se è dato un radicale con coefficiente diverso da 1, applicando la stessa regola è possibile portare dentro la radice il coefficiente per ottenere così una radice.

Se è dato un prodotto o un quoziente di radici, utilizzando la proprietà invariantiva è possibile operare la riduzione allo stesso indice delle due radici: ciò permette di scrivere sotto forma di radice il prodotto e il quoziente di due radici. Se

e

sono le due radici da moltiplicare, applicando la proprietà invariantiva si ottiene

Radici nel campo complesso

Se n ≥ 2 è un numero intero, si chiama radice complessa n-esima (o semplicemente radice n-esima) di un numero complesso z ogni numero complesso w tale che wⁿ{{{1}}}. Si veda il lemma → radice nel campo complesso.

Calcolo della radice quadrata aritmetica di un numero intero positivo

Esistono molti metodi per il calcolo manuale della radice quadrata di un numero intero positivo. Quello qui esposto è sostanzialmente dovuto a R. Bombelli che lo descrisse nella sua opera Algebra:

1. si scrive il radicando in uno schema simile a quello della divisione ponendolo a sinistra, mentre a destra si scriverà via via la radice che si va costruendo

2. si raggruppano le cifre a due a due procedendo da destra verso sinistra; il primo gruppo a sinistra è un numero che può avere una o due cifre

3. si calcola il più grande numero che elevato al quadrato è minore o uguale al numero del primo gruppo a sinistra (se ha una cifra può essere 1 o 2 o 3; se ha due cifre può essere da 4 a 9) e lo si trascrive a destra

4. si eleva al quadrato questa prima cifra della radice e la si sottrae al gruppo a sinistra; si abbassano altre due cifre del radicando ottenendo a sinistra un numero s e si moltiplica per 2 la radice fin qui trovata ottenendo un numero d che viene trascritto sotto:

5. si individua la cifra massima m che giustapposta a d fornisce un numero d′ che moltiplicato per m non superi s; tale numero è la nuova cifra della radice:

6. si sottrae d′ da s e si abbassano altre due cifre, ottenendo un nuovo numero s:

7. si moltiplica per 2 la radice fin qui ottenuta, la si trascrive sotto e si ripete il passo 5:

8. si ripete il passo 6 e poi il passo 7:

9. si ripete il passo 8; si ottiene sottraendo 0 e il numero dato è un quadrato perfetto; la sua radice quadrata è 1236. Qualora non si fosse ottenuto come risultato zero, si sarebbero ricercate cifre dopo la virgola, aggiungendo al radicando una virgola e due zeri e continuando la procedura allo stesso modo fino al numero di cifre decimali desiderato.

Per un altro significato del termine radice, che non ha riferimento con l’operazione di estrazione di radice, si veda il lemma → radice digitale.