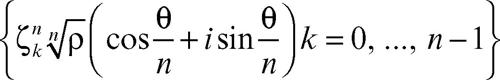radici n-esime dell'unita, gruppo delle
radici n-esime dell'unita, gruppo delle
radici n-esime dell’unità, gruppo delle insieme Cn delle n radici complesse di 1, dove n > 0 è un numero intero: l’insieme Cn è dotato della struttura di gruppo moltiplicativo e, rispetto a tale struttura, Cn è un gruppo ciclico di ordine n e quindi è isomorfo al gruppo additivo Zn delle classi resto modulo n. Servendosi della rappresentazione geometrica di C nel piano di → Argand-Gauss, le n radici n-esime dell’unità sono tutte poste su una stessa circonferenza centrata nell’origine e di raggio 1, ottenibili successivamente l’una dall’altra tramite una rotazione di un angolo di ampiezza 2π/n radianti: esse coincidono cioè con i vertici di un poligono regolare di n lati e di centro l’origine e con un vertice in (1, 0). Se
è la prima (in verso antiorario) radice n-esima dell’unità che segue 1, allora per la formula di de → Moivre essa genera per moltiplicazione tutto il gruppo Cn:
Ogni altra radice n-esima che, come ζn, genera il gruppo delle radici n-esime è detta una radice primitiva n-esima dell’unità: tali sono tutte e sole le radici della forma ζnk dove k è un intero coprimo con n. Il numero delle radici primitive n-esime dell’unità è pertanto φ(n), dove φ è la funzione di → Eulero. È possibile estendere la descrizione geometrica data delle radici n-esime dell’unità alle radici n-esime di un qualsiasi altro numero complesso z: esse sono tutte poste sulla circonferenza di raggio
centrata nell’origine e sono ottenibili successivamente l’una dall’altra tramite una rotazione di un angolo di ampiezza 2π/n radianti; esse coincidono cioè con i vertici di un poligono regolare di n lati centrato nell’origine. Nel caso in cui z è un numero reale positivo, allora una di tali radici è posta sul semiasse reale positivo e coincide con la radice aritmetica n-esima di |z|. Se z = ρ(cosθ + isinθ) è la rappresentazione goniometrica di z e se si considera la radice n-esima di z definita da
allora l’insieme delle radici n-esime di z è descritto come segue:
dove ζk è una qualsiasi radice primitiva n-esima dell’unità. Ciò si traduce nel fatto geometrico che l’n-agono i cui vertici sono le radici n-esime di z è ottenuto dall’n-agono i cui vertici sono le radici n-esime dell’unità tramite una rotazione di un angolo di ampiezza θ/n composta con una omotetia di rapporto
