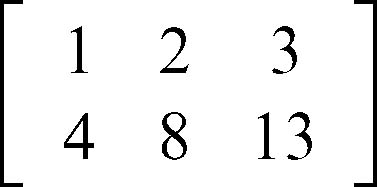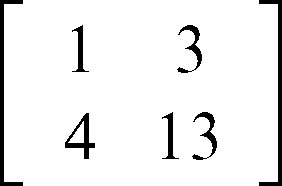rango

rango

rango termine che assume significati diversi a seconda del contesto. A parte il particolare significato in statistica (in cui si utilizza più frequentemente l’inglese → range), il significato generale del termine rimanda comunque a quello dell’algebra lineare, relativo alle matrici.

☐ In statistica, rango sta per posto occupato in un ordinamento e la → correlazione per ranghi, nonché il relativo coefficiente, fornisce un indice numerico per stabilire quanto siano “correlate” due graduatorie di differenti caratteri statistici quantitativi relativi agli stessi individui.

☐ In geometria, il rango è un’importante caratteristica delle → curve ellittiche.

☐ In analisi funzionale, per rango si intende il numero delle variabili indipendenti che compaiono in un’equazione funzionale; il rango denota anche l’insieme immagine del dominio di un operatore tra spazi funzionali.

☐ In algebra lineare, il rango di una matrice (o caratteristica) è il massimo ordine delle sottomatrici quadrate di determinante non nullo che si possono estrarre da una matrice data. Coincide con il massimo numero di righe (o colonne) linearmente indipendenti della matrice stessa. Per esempio, la matrice

ha rango 1 perché tutte le sue sottomatrici di ordine 2

hanno determinante nullo mentre almeno uno dei suoi minori di ordine 1 (in questo caso tutti) è diverso da zero. Invece, la matrice

ha rango 2, perché una sua sottomatrice di ordine 2

ha determinante 1 ⋅ 13 − 3 ⋅ 4 = 1, diverso da 0.

Di seguito sono elencate alcune proprietà del rango di una matrice (indicato qui con il simbolo «rk»), dove A^T e A^H indicano rispettivamente la trasposta e la trasposta coniugata di una matrice A (che, nel secondo caso, si suppone a coefficienti complessi):

• rk(A) = rk(A^T) = rk(A^H);

• se A è una matrice m × n, allora rk(A) ≤ min{m, n};

• se A è una matrice m × n (m > n), allora l’applicazione lineare indotta da A è iniettiva se e solo se rk(A) = n;

• se A è una matrice m × n (m < n), allora l’applicazione lineare indotta da A è suriettiva se e solo se rk(A) = m (l’applicazione lineare indotta da A è biiettiva se e solo se rk(A) = m = n);

• rk(A ⋅ B) ≤ min{rk(A), rk(B)};

• rk(A + B) ≤ rk(A) + rk(B);

• se A è una matrice quadrata di ordine n, allora il determinante di A è diverso da 0 se e solo se rk(A) = n.