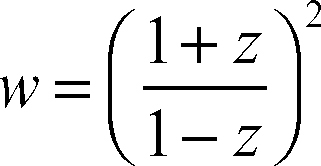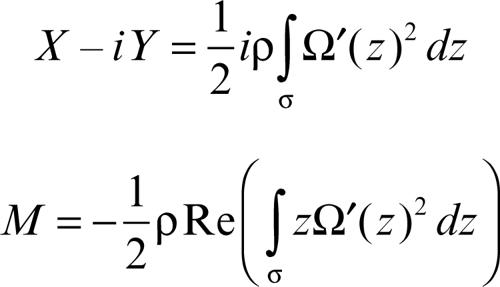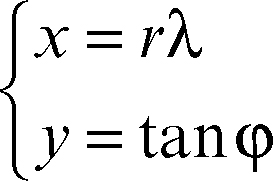rappresentazione conforme

rappresentazione conforme

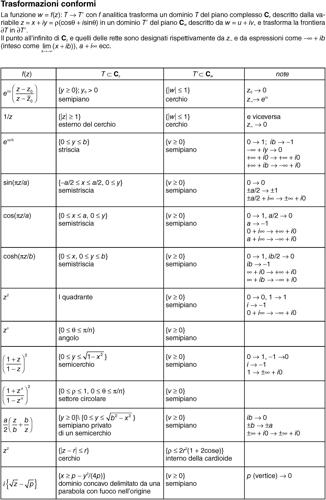
rappresentazione conforme in analisi, trasformazione w = ƒ(z) tra variabili complesse z = x + iy e w = u + iv, in cui ƒ è una funzione analitica con derivata non nulla. Una rappresentazione conforme gode della proprietà di conservare gli angoli, equivalendo localmente a una dilatazione di modulo |ƒ′ (z)| e a una rotazione di un angolo θ = arg(ƒ′ (z)). Poiché ogni funzione analitica G(w) è immagine di un’altra funzione g(ƒ(z)), la trasformazione permette di riportare un problema a configurazioni geometricamente più semplici, dove sia possibile avere una formula risolutiva. In particolare, poiché sia la parte reale sia il coefficiente della parte immaginaria di una funzione analitica sono funzioni armoniche, il metodo consente di risolvere l’equazione di → Laplace nel piano in geometrie relativamente complicate, riportandole al cerchio o al semipiano, dove vale la formula risolutiva di Poisson (→ Poisson, distribuzione di). Alcune semplici trasformazioni sono:

• w = e^πz/a tra la striscia 0 ≤ y ≤ a e il semipiano ν ≥ 0;

• w = sin(πz/a), tra la semistriscia −a/2 ≤ x ≤ a/2, 0 ≤ y e il semipiano ν ≥ 0;

tra il semicerchio 0 ≤ y ≤ √(1 − x ²) e il semipiano ν ≥ 0 (si veda anche le tavole delle trasformazioni conformi).

Nei punti in cui la derivata ƒ′ (z) ha uno zero di molteplicità n, gli angoli vengono moltiplicati del fattore (n − 1): per esempio la trasformazione w = z ² trasforma il primo quadrante 0 ≤ x, 0 ≤ y nel semipiano ν ≥ 0.

Le applicazioni (sempre bidimensionali), una volta molto diffuse anche se ora soppiantate da tecniche numeriche, riguardano problemi di fluidodinamica (filtrazione, flussi attorno a ostacoli), di elettrostatica, di trasmissione del calore in condizioni stazionarie. In tali applicazioni, particolari funzioni possono simulare le sorgenti dei campi interessati. Si parla in generale di potenziale complesso

dove Φ rappresenta il potenziale e le linee di livello Φ = α sono le linee equipotenziali, mentre le linee Ψ = β, perpendicolari alle precedenti, sono le linee di flusso. Si ha per esempio:

• Ω(z) = cz rappresenta il potenziale di un flusso uniforme;

• Ω(z) = kln(z − z₀) rappresenta una sorgente di intensità k nel punto z = z₀;

• Ω(z) = −ikln(z − z₀) rappresenta un vortice nel punto z = z₀;

• Ω(z) = μ/z rappresenta un dipolo nell’origine.

Particolarmente utili per l’aerodinamica sono le seguenti formule di Blasius, dal nome del fisico matematico tedesco Paul Richard Heinrich Blasius (1883-1970), che rappresentano le componenti X e Y della forza esercitata da un fluido di densità ρ su un ostacolo (un profilo alare) descritto da un ciclo σ e M ne è il momento rispetto all’origine:

☐ In cartografia, particolare rappresentazione, detta anche rappresentazione isogonica, la cui proprietà caratteristica è la conservazione degli angoli. Un esempio di rappresentazione conforme si ha nella proiezione di → Mercatore, le cui formule di corrispondenza sono:

dove λ e φ sono la latitudine e la longitudine di un punto sulla superficie terrestre. Tra le proiezioni che danno luogo a una rappresentazione conforme si possono ricordare inoltre la proiezione conica di → Lambert e la proiezione di Gauss-Boaga (→ cartografia).