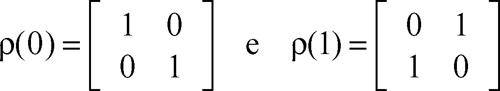rappresentazione
rappresentazione
rappresentazione termine che indica genericamente la presentazione sotto una determinata forma di un oggetto, una procedura o una struttura matematica (→ algoritmo, rappresentazione di un; → funzione, grafico di una; rappresentazione polare di un → numero complesso). I numeri, poi, hanno particolari rappresentazioni in un sistema di numerazione (→ sistema di numerazione posizionale) e all’interno di uno strumento automatico di calcolo (→ numero macchina). Tutti gli ordinari insiemi numerici ammettono una rappresentazione geometrica: → N (insieme dei numeri naturali), → Z (insieme dei numeri interi), → Q (insieme dei numeri razionali) come sottoinsiemi di punti della retta; → R (insieme dei numeri reali) con i punti della retta; → C (insieme dei numeri complessi) con i punti del piano di Argand-Gauss. In geometria piana e solida si hanno la rappresentazione conforme, che conserva gli angoli, e la rappresentazione equivalente, che conserva le aree. Nella teoria degli insiemi, un insieme può essere rappresentato tramite un diagramma di → Eulero-Venn. In algebra e in analisi, si può ricordare la rappresentazione parametrica come relazione algebrica fra i punti di una curva, o di una superficie, e un opportuno parametro. In geometria descrittiva le varie rappresentazioni si distinguono per i metodi adottati: metodo delle proiezioni ortogonali o di Monge, metodo delle proiezioni quotate, metodo delle proiezioni centrali, o altri metodi derivati dall’assonometria e dalla prospettiva.
Rappresentazione di un gruppo G su uno spazio vettoriale V
Omomorfismo ρ di un gruppo G nel gruppo Aut(V) degli automorfismi di V. Per esempio, una rappresentazione del gruppo Z2 è l’omomorfismo ρ: Z2 → Aut(R2) definito da
Tale rappresentazione identifica 0 con l’identità e 1 con l’automorfismo che scambia le due componenti di un vettore. Supposto V di dimensione finita, qualunque sia il campo su cui V è definito, Aut(V) è dotato della struttura di gruppo algebrico; se inoltre V è uno spazio vettoriale reale o complesso, allora Aut(V) è dotato della struttura di gruppo di Lie. Nel caso in cui G sia un gruppo di Lie, un gruppo algebrico o più in generale un gruppo topologico, si richiede allora che la rappresentazione ρ preservi tale struttura: si definisce così una rappresentazione di un gruppo G di Lie (rispettivamente un gruppo algebrico, un gruppo topologico) in uno spazio vettoriale V come una rappresentazione di G su V che sia al contempo un’applicazione differenziabile (rispettivamente regolare, continua) rispetto alla struttura di varietà differenziabile (rispettivamente di varietà algebrica, di spazio topologico) di Aut(V).
Un G-modulo è uno spazio vettoriale dotato di una rappresentazione di G; un sottomodulo W di un G-modulo V è un suo sottospazio vettoriale preservato dall’azione di G; cioè tale che, per ogni g di G e per ogni w di W, ρ(g)(w) appartiene a W. La rappresentazione di G sul sottomodulo W indotta da ρ è invece detta sottorappresentazione di ρ. Un G-modulo è detto irriducibile se è privo di sottomoduli non banali (distinti cioè da quello costituito dal solo elemento nullo o da quello costituito dall’intero G-modulo). Due rappresentazioni ρ1: G → Aut(V1) e ρ2: G → Aut(V2) di uno stesso gruppo G sono dette isomorfe se esiste un isomorfismo φ: V1 → V2 tale che ρ2(g)(φ(ν)) = φ(ρ1(g)(ν)), per ogni g appartenente a G e per ogni ν appartenente a V.
Rappresentazione di un’algebra A (definita su un campo K) su uno spazio vettoriale V (definito sullo stesso campo K)
Similmente al caso di un gruppo, si definisce come un omomorfismo di algebre ρ: A → End(V) nell’algebra degli endomorfismi di V. Nel caso in cui A sia un’algebra di Lie, si definisce una rappresentazione di A su uno spazio vettoriale V come un omomorfismo di algebre di Lie ρ: A → γλ(V) nell’algebra di Lie degli endomorfismi di V, dotata del prodotto definito dal bracket [a, b] = ab − ba. Tutte le definizioni date nel caso di un gruppo, come quella di modulo, di modulo irriducibile, di sottomodulo e sottorappresentazione, sono similmente riformulate nei casi di un’algebra e di un’algebra di Lie.