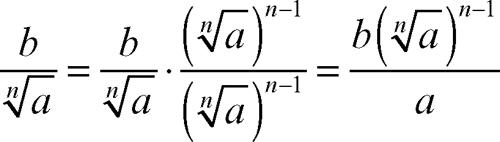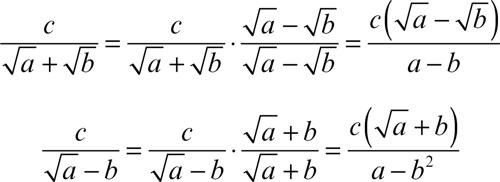razionalizzazione
razionalizzazione
razionalizzazione procedura che, in alcuni casi, consente di riscrivere una espressione frazionaria contenente radicali al denominatore in una forma equivalente, in cui però i radicali compaiano solamente al numeratore. Per esempio:
Il motivo di tale trasformazione consiste nel fatto che spesso l’estrazione di radice, come nell’esempio, produce un numero irrazionale e, se esso compare al dividendo, tale dividendo deve essere approssimato già al primo passo dell’algoritmo della divisione; se invece il numero irrazionale compare al numeratore si può effettuare la divisione con l’approssimazione che si vuole. Di seguito sono esposti alcuni casi particolari in cui è possibile razionalizzare una espressione frazionaria.
• Se il denominatore è costituito da un’unica radice quadrata, allora si moltiplicano il numeratore e il denominatore per la radice quadrata che compare al denominatore della frazione stessa:
• Se il denominatore è costituito da un’unica radice non quadrata e se n è l’indice di tale radice, allora si moltiplicano il numeratore e il denominatore per la radice che compare al denominatore della frazione stessa, elevato alla n − 1:
• Se il denominatore è la somma (rispettivamente, la differenza) di due termini, di cui uno o entrambi sono radici quadrate, allora, utilizzando il prodotto notevole che esprime la differenza di due quadrati, basta moltiplicare il numeratore e il denominatore per la differenza (rispettivamente, la somma) dei due termini che compaiono al denominatore della frazione stessa, come nei seguenti esempi: