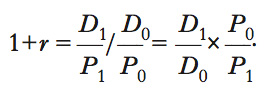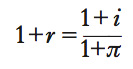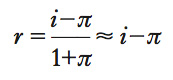reale

reale

Il valore r. di una grandezza al tempo t si esprime mediante il rapporto tra il valore monetario o nominale della medesima grandezza al tempo t e l’appropriato indice dei prezzi correnti (P_t). Un qualsiasi paniere di beni e servizi (y_1t, y_2t,…y_nt) ha un valore monetario espresso da

dove P_t è un indice dei prezzi ideale (➔ prezzo). Il valore r. di tale paniere è allora Y^m_t/P_t=Y_t. ● Il salario reale W_t/P_t si ottiene utilizzando come P_t l’Indice dei Prezzi al Consumo (IPC). ● La quantità r. di moneta esprime il potere d’acquisto dello stock di moneta M_t ed è dato da M_t/P_t, dove P_t può essere sia il deflatore del PIL (➔ ) sia l’IPC. ● Il tasso di interesse r. (r) misura quanti beni possono essere acquistati in più tra un anno rinunciando alla spesa di un euro oggi (t=0) e prestando quell’euro al tasso di interesse nominale i. Se si pospone il consumo odierno di y₀ a tra un anno (t=1), sarà possibile comprare la quantità y₁=y₀+ry₀=y₀ (1+r). Con prezzi costanti, rinunciando a spendere oggi la somma D₀, si potrebbe acquistare tra un anno, con la somma D₁, la quantità q₁ ancora al livello dei prezzi p₀. Da cui si ricava 1+i=(D₁/D₀)=(y₁/y₀)=1+r, quindi i=r. La coincidenza tra tasso di interesse r. e nominale scompare se i prezzi variano da un anno all’altro, cioè se c’è inflazione. Il tasso di inflazione tra l’anno 0 e l’anno 1 è: π=(P₁/P₀)−1, quindi (P₁/P₀)=1+π. Il rapporto tra le quantità acquistabili al tempo 1 e al tempo 0, quando i prezzi mutano, è

Sostituendo 1+i al posto di D₁/D₀ e 1/(1+π) al posto di P₀/P₁, si deriva:

e quindi il tasso di interesse r. come:

cioè come differenza tra tasso di interesse nominale e tasso di inflazione.