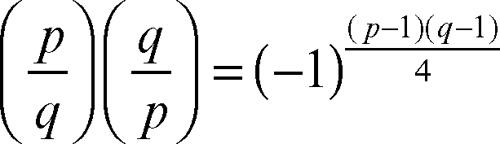reciprocita quadratica, legge di
reciprocita quadratica, legge di
reciprocità quadratica, legge di o teorema aureo, teorema di aritmetica modulare, congetturato inizialmente da Eulero nel 1783 e dimostrato definitivamente da C.F. Gauss nel 1796 (che appunto lo definì aureum theorema), dopo una dimostrazione fallace di A.M. Legendre nel 1785. Esso stabilisce che se p > 2 e q > 2 sono due primi distinti non entrambi congrui a 3 modulo 4, allora p è un residuo quadratico modulo q se e solo se q è un residuo quadratico modulo p. Equivalentemente, esiste un numero intero x tale che x 2 è congruente a p (modq) se e solo se è congruente anche a q (modp). Viceversa, se p e q sono entrambi congruenti a 3 modulo 4, allora solamente uno tra p e q è un residuo quadratico modulo l’altro. La legge di reciprocità quadratica può essere espressa formalmente usando il simbolo di Legendre
il quale, se s e t sono primi distinti maggiori di 2, vale 1 se s è un residuo quadratico modulo t e −1 altrimenti:
Vi sono leggi di reciprocità che vanno oltre il secondo grado (reciprocità cubica, quartica ecc.), ma in tali casi si pone il problema di operare oltre il campo Q dei numeri razionali. Il problema della dimostrazione della più generale legge di reciprocità in ogni campo numerico è il nono dei problemi posti da D. Hilbert nella sua famosa lista di problemi del 1900 (→ Hilbert, problemi di).