refutazione

refutazione

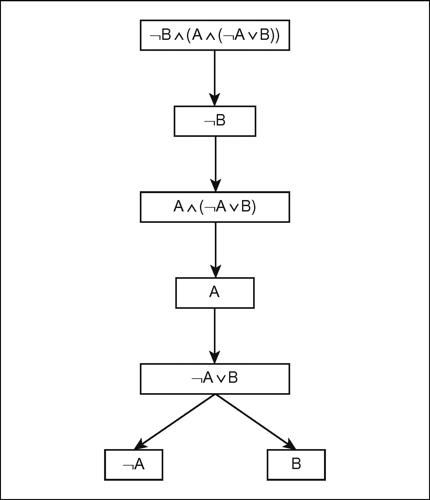
refutazione di una formula in un sistema formale, è la dimostrazione della sua negazione. In un sistema formale, se una formula A non è deducibile e non è refutabile (cioè anche non A non è deducibile) allora la formula è indecidibile (→ decidibilità). Più in generale, il termine può riferirsi alla non accettazione di una congettura, che può essere refutata esibendone un controesempio. Un metodo per determinare se una proposizione va refutata consiste nella costruzione dell’albero di refutazione. L’albero si costruisce a partire da una radice in cui si pone, come etichetta, la formula da refutare e si costruiscono successivi rami tenendo conto della struttura della formula in esame. Per esempio, nel calcolo delle proposizioni si utilizzano queste regole per la costruzione dell’albero:

a) se in un nodo c’è una proposizione atomica A o la sua negazione ￢A, non si prosegue;

b) se in un nodo c’è una congiunzione, A ∧ B, si prosegue con due nodi successivi rispettivamente etichettati con A e B;

c) se in un nodo c’è una disgiunzione, A ∨ B, dal nodo si divaricano due rami nei cui nodi terminali si pongono come rispettive etichette A e B;

d) se compare una implicazione, A ⇒ B, la si sostituisce con l’equivalente logica ￢A ∨ B e si prosegue come in c);

e) se compare una doppia implicazione, A ⇔ B, la si sostituisce con l’equivalente logica

e si prosegue come in b) o c).

Si chiude l’albero quando tutti i nodi terminali sono proposizioni atomiche o loro negazioni. La formula in esame va refutata se e solo se in tutti i percorsi che vanno dai nodi terminali alla radice compaiono tutte le proposizioni atomiche componenti la formula data e tutte le loro negazioni.