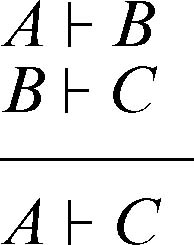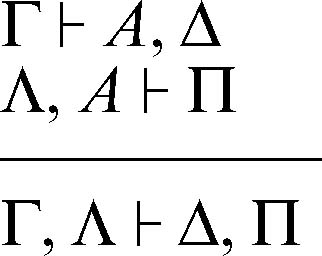taglio, regola del

taglio, regola del

taglio, regola del (in inglese cut rule) una delle regole di derivazione del calcolo dei → sequenti che può essere esplicitata come segue: se da una premessa A è possibile trarre una conclusione B e se, usando B come premessa, è possibile derivare da B una conclusione C, allora è possibile passare direttamente da A a C; in formule:

Questa regola è detta regola del taglio perché nella deduzione finale A ⊦ C la formula B non compare più; è stata quindi “tagliata”. La regola è esprimibile in termini più generali, indicando con Γ, Δ, Λ, Π formule ben formate di un linguaggio logico e interpretando la scrittura Γ ⊦ Δ come l’esistenza di una deduzione che porti dalle premesse Γ alle conseguenze Δ (se tutte le formule di Γ sono vere allora almeno una delle formule di Δ è vera):

Rispetto alle altre regole del calcolo dei sequenti, la regola del taglio ha un aspetto singolare legato alla sua irreversibilità; infatti, analizzando la deduzione finale non è possibile risalire a quale formula sia stata “tagliata”. Ciò significa che in una dimostrazione in cui si fa uso della regola del taglio non si possono stabilire in modo automatico i passaggi che portano dall’assioma identità alla deduzione finale. A questo proposito acquista un’importanza centrale il teorema di eliminazione del taglio dimostrato da G. Gentzen nel 1934, che stabilisce che è possibile trasformare ogni dimostrazione di un sequente Γ ⊦ Δ in una dimostrazione dello stesso sequente in cui non si faccia uso della regola del taglio. In altri termini, ciò significa che è possibile associare a ogni dimostrazione un’altra dimostrazione in cui non si faccia uso di → lemmi. Questo risultato non ha utilità nella pratica delle dimostrazioni matematiche, in cui si fa largamente uso di lemmi. La sua importanza deve essere invece vista in relazione alla possibilità di “automatizzare” una dimostrazione; il teorema di eliminazione del taglio stabilisce, infatti, che le deduzioni del calcolo dei sequenti sono paragonabili a procedure algoritmiche e crea pertanto un legame fra la teoria della dimostrazione e l’informatica teorica. Questo legame è sancito dall’isomorfismo di → Curry-Howard.