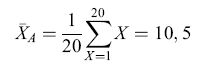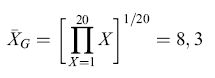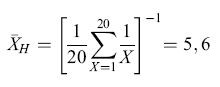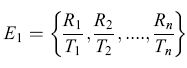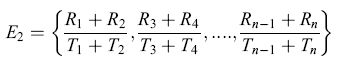Regole funzionali per decidere
Regole funzionali per decidere
La rappresentazione accurata ed effìciente dell'ambiente nel quale un organismo vive richiede abilità nell'elaborare le informazioni cognitive che sembrano basate su regole semplici. Attraverso l'evoluzione per selezione naturale queste regole dovrebbero essersi strutturate in modo tale da aumentare l'abilità di un organismo a riprodursi e a sopravvivere nel proprio ambiente. Illustrerò la natura di queste regole funzionali esaminando le basi computazionali della ricerca e della scelta di possibili partner sessuali, della scelta delle risorse di cui nutrirsi e della strutturazione delle interazioni sociali che portano alla cooperazione. Alla fine si dovrebbe essere capaci di legare una specifica regola computazionale a un meccanismo nervoso che renda effettiva la regola. Uno studio comparativo delle regole che emergono come funzionali e dominanti può anche rivelare alcune caratteristiche comuni a comportamenti evolutisi sulla base di regole.
Il comportamento governato da regole
Nella loro lotta per la sopravvivenza e la riproduzione tutti gli organismi affrontano il difficile compito di ottenere risorse essenziali come il cibo, un rifugio, un partner sessuale. Nel corso dell'evoluzione la selezione naturale dovrebbe favorire quegli organismi capaci di agire in modo efficiente per aumentare la probabilità di acquisire e utilizzare queste risorse. Spesso il comportamento di un organismo sembra essere basato su regole, cioè esso si attua come un pattern di risposte a specifiche condizioni ambientali che possono essere descritte da una regola. Quella che chiamerò regola funzionale è dunque una regola che, quando applicata coerentemente nel corso della risposta comportamentale di un individuo all'ambiente, ne aumenta le possibilità di sopravvivenza e di riproduzione all'interno di quell'ambiente. Tali regole possono essere applicate inconsciamente e possono figurare come risposte automatiche codificate nel sistema nervoso dell'organismo. Per esempio, se scendendo da un marciapiede improvvisamente arrivasse un'automobile, si potrebbe seguire questa regola: saltare indietro nella direzione che rende massima la distanza tra il punto di atterraggio e il piano in cui si muove l'automobile. Seguendo tale regola la probabilità di collisione e di danno fisico sarebbe minima. Esistono regole antagoniste che non minimizzano il danno fisico, per esempio, saltare nel piano in cui si muove la macchina. Questa regola massimizza la probabilità di danno fisico ed è chiaramente poco adattativa (a meno che non si voglia riscuotere un grande premio assicurativo). Si potrebbe anche saltare indietro lungo la traiettoria in cui si stava camminando. Questa regola minimizza il danno fisico solo se inizialmente si camminava perpendicolarmente rispetto alla direzione della macchina. Qualunque regola che non renda minima la probabilità di essere colpiti non è funzionale. La mia osservazione casuale delle risposte della gente (incluse le mie) è che in realtà seguiamo una regola funzionale e così saltiamo in modo tale da massimizzare la distanza tra il piano in cui si muove la macchina e il nostro punto di atterraggio. Non lo facciamo consciamente, né eseguiamo una serie di calcoli. Semplicemente reagiamo. Tuttavia le nostre risposte possono essere espresse come una regola stabilita e questa regola sembra essere incorporata nella fenomenologia di base dell'elaborazione delle informazioni da parte del sistema nervoso. Il comportamento governato da regole è caratterizzato da due processi fondamentali: la codificazione e la computazione (Gallistel, 1990). L'informazione che proviene dall'ambiente è convertita tramite i sensi in una forma codificata che può essere manipolata e immagazzinata sulla base di specifiche regole computazionali. L'applicazione di una serie di regole computazionali a una specifica serie di dati sensoriali genera una specifica serie di risposte o azioni. Conoscendo le regole e le percezioni sensoriali dell'organismo possiamo prevedere le risposte comportamentali. Certamente il compito più difficile è scoprire quali sono le regole di base che governano specifici tipi di risposte. Le regole che sono incorporate all'interno del sistema nervoso dell'organismo si sono evo Iute e sono soggette alla selezione naturale in modo analogo a qualsiasi altro aspetto del fenotipo dell'organismo. Già ai tempi di Charles DaIwin era stato osservato che devono esservi state un'origine e una differenziazione evolutive nelle funzioni mentali. Recentemente si è andato sviluppando un considerevole interesse nei confronti delle implicazioni dell'evoluzione e della selezione naturale che riguardano le capacità e le limitazioni cognitive di un organismo. Mentre molti studi documentano la variazione dei gradi di specializzazione adattativa nella funzione cognitiva, pochi studi esplorano la natura adattativa di specifiche regole computazionali come aspetti dell'architettura funzionale cognitiva di un organismo.
Almeno in linea di principio differenti algoritmi computazionali possono generare una selezione differenziale, sia influenzando l'efficienza e l'accuratezza della stima sia producendo differenti rappresentazioni dell'ambiente. Come esempio dell'efficienza algoritmica riguardante le regole funzionali si consideri il seguente problema: sommare i numeri tra 1 e 100. Il metodo che la maggior parte di noi seguirebbe nell'affrontare questo problema sarebbe sommare semplicemente i numeri in sequenza. Uno più due uguale tre, più tre uguale sei, più quattro uguale dieci, e così via fino ad arrivare a 5050, che è la risposta. In alternativa, si potrebbe notare che 1 più 100 è uguale a 101, 2 più 99 è uguale a 101, 3 più 98 è uguale a 101 e vi sono 50 coppie di somme di questo tipo. Così la risposta è 50 volte 101, che è uguale a 5050. Entrambi i metodi danno la stessa risposta, ma il secondo metodo è chiaramente più efficiente e più rapido del primo. Se tentassimo di effettuare questo calcolo nella nostra testa, il secondo metodo sarebbe probabilmente anche il più accurato. Questo esempio illustra come differenti schemi computazionali possano avere differenti gradi di efficienza e accuratezza nell'operazione mentale. Presumibilmente la selezione opera per aumentare l'efficienza e l'accuratezza delle computazioni essenziali che riguardano comportamenti con immediate conseguenze evolutive, come procurarsi il cibo o scegliere un partner.
Differenti regole computazionali possono dare origine a rappresentazioni molto differenti dell'ambiente che possono essere decisive per attuare le azioni e le decisioni appropriate. Per esempio, la tendenza centrale in una serie di eventi che possono formare le basi per l'aspettativa della ricompensa di un animale può essere rappresentata da una serie di computazioni. Consideriamo la tendenza centrale di una popolazione di fiori dove le ricompense in nettare per l'animale sono conformi a una distribuzione uniforme tra l /lI e 20 mI. Le tre misure più comuni della tendenza centrale, la media aritmetica (XA), la media geometrica (XG) e la media armonica (XH), generano tre diverse misure e possono potenzialmente portare a scelte e decisioni molto differenti:
formula [
l]
formula [2]
formula. [3]
Quale delle tre particolari rappresentazioni della tendenza centrale corrisponda meglio al modello osservato può dipendere dalla specificità del compito. Per esempio, la media aritmetica dei tassi di guadagno netto di energia può caratterizzare la scelta floreale nei bombi (Real, 1992), mentre la media armonica dei ritardi tra prove successive può essere usata da storni che prendono decisioni sul foraggiamento in camere operanti (Reboreda e Kacelnik, 1991). Come si può vedere dalle equazioni per le tendenze centrali, in alcuni casi i valori possono essere correlati. Per esempio, minimizzare il ritardo (X) nella media armonica equivale a stimare la massimizzazione del tasso nella media aritmetica dal momento che 1/X è un tasso. Quale delle possibili rappresentazioni della tendenza centrale sia effettivamente usata può dipendere da ragionamenti di carattere generale a favore dell'applicabilità di ciascun tipo di metodo per costruire una media. Per esempio, la media geometrica può rappresentare al meglio i sistemi con effetti che si combinano, come l'accrescimento. La media aritmetica può essere impiegata al meglio in situazioni dove le ricompense sono distribuite spazialmente. In tal modo la selezione naturale può portare all'uno o all'altro metodo di rappresentazione computazionale a seconda del particolare compito o problema affrontato dall'organismo.
Nella restante parte di questo saggio discuterò alcuni esempi dei comportamenti decisionali che sembrano governati, o almeno possono essere spiegati, da regole funzionali.
Regole per trovare un partner
Per introdurre il metodo generale che serve a formulare ed esplorare le conseguenze evolutive delle differenti regole funzionali consideriamo il problema generale della scelta del partner. La quantità di prole che un individuo genera nel corso della vita è solitamente considerata la misura più diretta del successo evolutivo. Di conseguenza, la selezione naturale può favorire la formazione di regole funzionali che governano le scelte che gli individui compiono in base al loro pattern di ricerca e di scelta tra potenziali partner. Le specie a sessi distinti, come quella umana, devono trovare membri del sesso opposto, e successivamente accoppiarsi con loro, per essere rappresentati geneticamente nelle generazioni future.
In una pubblicazione di notevole impatto scientifico, A.C. Janetos (1980) fece notare che ciò che può costituire la miglior regola funzionale per la scelta del partner dipende dal repertorio comportamentale dell'individuo. Per illustrare questo punto, egli esaminò quattro regole alternative, tramite le quali gli individui potevano prendere decisioni sui partner da scegliere. L'obiettivo principale nello studio di Janetos fu quello di determinare se esista una regola di scelta dominante che, quando seguita, generi una più alta aspettativa di successo evolutivo rispetto ad altre possibili regole. Alcune regole per operare una scelta sul partner possono essere migliori di altre quando sono attuate sullo stesso pattern di informazioni disponibili. Dai vantaggi, che è possibile postulare, associati a ciascuna regola decisionale, possiamo dedurre il comportamento migliore che dovrebbe essere adottato dall'organismo.
In primo luogo immaginiamo che in una data popolazione un sesso (di solito quello maschile) cerchi attivamente il compagno, mentre l'altro sesso (di solito quello femminile) accetti passivamente le offerte per l'accoppiamento. La passività, tuttavia, varia da individuo a individuo a seconda delle loro qualità. Per esempio, in molte specie di pesci i maschi sollecitano attivamente le femmine all'accoppiamento e le femmine sono passive. Tuttavia, le femmine differiscono tra loro nella dimensione, che in questi animali è un indice abbastanza valido della quantità di prole che può produrre una femmina. Così un pesce maschio che si accoppia con una femmina molto grande avrà molti figli; invece lo stesso maschio che si accoppiasse con una femmina più piccola produrrebbe un minor numero di figli. Ovviamente è nell'interesse evolutivo del maschio accoppiarsi con una femmina più grande possibile. Janetos propose quattro regole funzionali che dovrebbe seguire un individuo che cerca di accoppiarsi. La prima regola assume che la scelta di un compagno sia casuale. Un individuo in cerca di un compagno incontra casualmente potenziali partner e accetta il primo membro del sesso opposto incontrato. Il vantaggio medio per il maschio è dunque determinato dalla qualità media delle femmine disponibili. La seconda regola assume che il maschio in cerca di una partner possieda il criterio della soglia fissa (fixed-threshold criterion) sopra il quale una femmina incontrata è giudicata accettabile e sotto il quale la femmina è considerata inaccettabile. Per esempio, un pesce maschio potrebbe basarsi su una dimensione critica limite per accettare una femmina. La terza regola, la regola della migliore delle n (best-of-n-rule) immagina che i maschi passino in rassegna un certo numero fisso (n) di potenziali compagne femmine e poi selezionino le femmine di qualità migliore tra tutti gli n individui esaminati. l maschi sono liberi di tornare da qualunque femmina precedentemente incontrata e possono anche ricordare la qualità e il luogo d'incontro di tutte le femmine incontrate prima. In questa regola, la variabile decisionale è il numero delle femmine esaminate (n) prima che la scelta sia operata. La quarta e ultima regola che Janetos passò in rassegna, la regola del primo incontro (one-step decision rule), assume che i maschi accettino o rifiutino femmine nel momento in cui le incontrano. Se la femmina è rifiutata, il maschio continua a cercare. La ricerca termina e l'accoppiamento ha luogo quando la qualità della femmina supera la qualità attesa delle femmine incontrate nel corso di una ricerca continuata. In questa regola, la variabile decisionale è una soglia ottimale di qualità che fa terminare la ricerca.
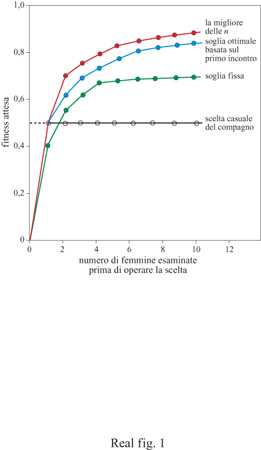
Ciascuna di queste quattro regole funzionali può essere rappresentata in una esplicita forma matematica e, per ogni data distribuzione di qualità delle femmine, può essere calcolato il valore evolutivo atteso (fitness) per il maschio. Ciascuna delle quattro regole funzionali mostra un aumento nel valore evolutivo per il maschio quando il maschio aumenta il numero delle femmine esaminate (fig. 1). Tuttavia, qualunque siano le dimensioni del campione, si osserva una chiara gerarchia nella prestazione relativa delle regole seguite.
La scelta casuale è chiaramente una strategia perdente. Il maschio può sempre fare di meglio con una delle altre tre strategie. Con gli assunti dei modelli così formulati da Janetos la migliore strategia per tutte le dimensioni del campione è la regola della migliore delle n. Dal momento che ciascuna delle quattro strategie mostra anche profitti decrescenti per ogni femmina che viene aggiunta al campione (cioè la curva della fitness tende a diminuire quando la dimensione del campione aumenta), l'autore concluse che la strategia migliore in assoluto per un maschio è quella di esaminare approssimativamente cinque o sei femmine e poi scegliere la migliore tra quelle esaminate. La sua conclusione è stata ampiamente considerata come lo scenario più plausibile per la scelta del partner.
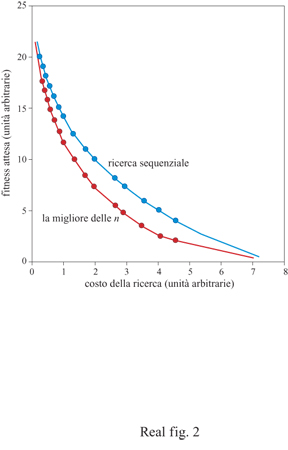
Tuttavia, il valore delle regole funzionali può drasticamente cambiare se modifichiamo alcuni assunti sul comportamento dell'organismo. Janetos ha trascurato un'importante caratteristica nel problema della scelta del partner, cioè il costo della ricerca e della scelta. Non sarebbe sorprendente che, nel caso di costi minimi, la migliore delle n fosse la regola dominante su tutte le altre. Infatti, dal momento che esaminare non è costoso, la migliore strategia è quella di passare in esame tutti i potenziali partner della popolazione e poi scegliere il migliore della popolazione. Comunque, il costo di esaminare partner è spesso piuttosto elevato e i partner rifiutati potrebbero non essere più disponibili in futuro. Quando i costi della ricerca vengono aggiunti al problema della scelta del partner, il valore delle differenti regole cambia drasticamente. Nel 1990 ho presentato modelli modificati di scelta del partner che tengono conto dei costi della ricerca (Real, 1990). La matematica dei modelli è piuttosto complessa, ma le regole essenziali per la scelta sono semplici. Per la regola della migliore delle n, il numero dei partner presi in esame aumenta fino al punto in cui la grandezza del campione è superiore al costo di una ricerca supplementare. Per la regola della ricerca sequenziale (sequential search rule) la soglia critica dell'accettazione è fissata in modo da eguagliare il costo della ricerca con il guadagno atteso della fitness proveniente da una ricerca supplementare. Quando queste regole sono confrontate, la regola della ricerca sequenziale prevale sulla regola della migliore delle n se si considerano i costi della ricerca, giungendo così a una conclusione opposta a quella raggiunta da Janetos dieci anni prima (fig. 2).
Quando sussistono costi di ricerca (cosa sempre probabile), la superiorità della ricerca sequenziale è facile da osservare. Nella regola della migliore delle n coloro che cercano devono esaminare un numero fisso di potenziali partner, senza tener conto della qualità degli individui incontrati precedentemente nella sequenza in esame. Se si incontra un partner di altissima qualità all'inizio di tale sequenza, si dovrà passare oltre a mano a mano che la ricerca procede e ciò può comportare costi molto elevati. Tuttavia la regola della ricerca sequenziale è flessibile e sensibile alla qualità della compagna incontrata. Se la compagna incontrata è di qualità molto alta, la ricerca si ferma e non vengono accumulati costi addizionali.
Attualmente sono in corso indagini sperimentali e di laboratorio sulle esatte regole utilizzate nella scelta del partner. Gran parte degli esperimenti attuali è volta a valutare il tipo di regola funzionale utilizzata nelle attività di ricerca del partner. È ancora troppo presto per stabilire se la regola seguita dagli organismi sia la migliore delle n o la scelta sequenziale. Comunque, le indagini teoriche, del tipo di quelle effettuate da Janetos, costituiscono il primo passo per individuare le regole funzionali più probabili. Forse il problema che viene risolto con maggior successo tramite regole funzionali distinte è quello sul modo in cui gli organismi effettuano scelte sulle risorse da usare. Esaminiamo ancora i bombi come modello di analisi delle regole funzionali.
Regole per la scelta delle risorse
Ogni animale deve trovare il cibo per procurarsi i fattori nutritivi essenziali e l'energia richiesta per crescere e riprodursi. In molte specie di insetti che si posano sui fiori per succhiare il nettare esiste un legame diretto tra la raccolta delle risorse e la riproduzione. Nei bombi, per esempio, singole regine nascono in primavera, formano un nido, raccolgono nettare e polline e depongono uova. Le uova sono deposte all'interno del nido e crescono sul cibo ammassato, costituito da una mistura di polline e nettare assemblati dalla regina stessa, la quale depone più uova; la colonia si ingrandisce non appena nascono le operaie che raccolgono più nettare e polline. La grandezza e il successo riproduttivo della colonia sono direttamente legati alla capacità delle operaie foraggiatrici di raccogliere cibo. Dal momento che in questi insetti il successo evolutivo è legato alla raccolta del cibo, la selezione naturale ha probabilmente favorito la formazione di regole funzionali che portano a un'efficienza delle operaie in questa operazione.
In natura, in tutte le stagioni vi sono in genere molte specie di piante che fioriscono. Quale tipo di fiore dovrebbe visitare una foraggiatrice? Dovrebbe semplicemente visitare qualsiasi tipo di fiore incontrato, a caso, oppure una serie di tipi di fiori, in base a qualche criterio di efficienza energetica? Nel 19° secolo i naturalisti osservarono che molto spesso le api sembrano orientarsi su un solo tipo di fiore per volta e limitano le loro visite solo a quel tipo. Questo tipo di comportamento è stato denominato specializzazione (majoring). Di conseguenza se le api si specializzano su un singolo tipo di fiore, qual è la regola per scegliere un tipo di pianta piuttosto che un altro tipo che fiorisce contemporaneamente? Dal momento che le api dipendono dall'energia e dai fattori nutritivi per la riproduzione, le foraggiatrici potrebbero scegliere quei fiori che offrono una quantità maggiore di nettare e polline. Se a un'ape fosse concesso di scegliere tra fiori che offrono 1 μI di nettare ciascuno e fiori che ne offrono 5 μI, essa sceglierebbe quasi certamente il tipo di fiore con la ricompensa più alta. Tuttavia, in natura i fiori non sono uniformi nella ricompensa in nettare che forniscono, ma mostrano una considerevole variabilità. Come fa un'ape a scegliere quando è presente variabilità nella grandezza della ricompensa dei fiori?
Si tratta di un problema abbastanza simile a quello di un essere umano che compia un investimento nella scelta tra differenti azioni finanziarie. Alcune saranno caratterizzate da un profitto mediamente alto, ma con un elevato grado di incertezza, mentre altre saranno caratterizzate da profitti mediamente bassi, ma con un grado di incertezza inferiore. È stato riconosciuto per molti anni che gli investitori, in genere, si trovano di fronte al conflitto tra rese elevate e alto grado di incertezza e che le azioni molto incerte saranno scelte solo se accompagnate da un' attesa di profitto molto alta.
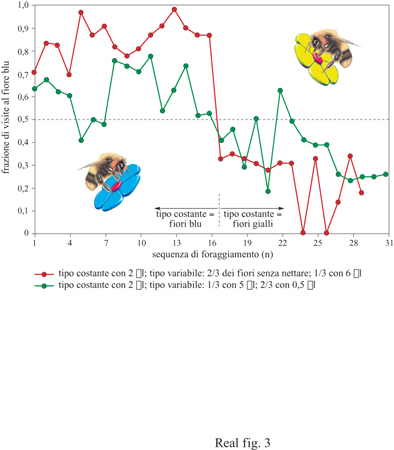
Nel 1980 ho effettuato un esperimento con i bombi in cui veniva concessa la scelta tra un tipo di fiore blu con una ricompensa costante e un tipo di fiore giallo con una ricompensa variabile, ma in media uguale a quella presentata dal fiore blu. I bombi hanno scelto nettamente il fiore con ricompensa costante rispetto a quello con ricompensa variabile (fig. 3).
Questo tipo di comportamento, in cui gli animali scelgono l'alternativa con ricompensa costante rispetto a quella con ricompensa variabile (con uguale attesa), è stato chiamato avversione per il rischio e sembra ampiamente diffuso. L'avversione per il rischio è stata ora documentata in api, vespe, uccelli, piccoli mammiferi e nella specie umana. Esistono numerosi modelli funzionali che rappresentano le risposte di avversione per il rischio (Bateson e Kacelnik, 1996). Di seguito, presenterò un resoconto basato sulla formazione di regole funzionali per l'elaborazione delle informazioni nelle singole api foraggiatrici e discuterò come queste regole potrebbero essere incorporate in specifiche strutture neuronali.
Una regola funzionale per la scelta del fiore
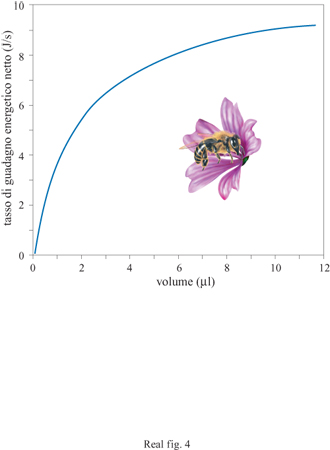
Quando un'ape visita un fiore, ingerisce una quantità fissa di nettare (espressa in microlitri) che si trasforma in una ricompensa energetica (espressa in joule) basata sul contenuto di zucchero del nettare. Nel 1987 L. Harder e io abbiamo dimostrato che per un'ape il tasso di guadagno energetico netto era una funzione non lineare del volume di nettare. Quando l'ape ingeriva più nettare, il tasso marginale del guadagno energetico decresceva (fig. 4). Questa semplice relazione non lineare tra volume di nettare e tasso di guadagno energetico è sufficiente a spiegare il modello di avversione per il rischio nelle api. Immaginiamo che un'ape possa raccogliere cibo da due tipi di fiori: blu e gialli. Da quelli blu l'ape riceve una quantità costante di 2 μI di nettare, mentre da quelli gialli può ricevere sia 4 μI sia 0 μI con uguale probabilità. Harder e io abbiamo proposto che l'ape scelga il tipo di fiore che produce il più alto tasso medio di ricompensa energetica e ciò costituisce un problema di notevole interesse.
Vi sono diverse regole funzionali alternative che potrebbero essere elaborate per comprendere come le api calcolino il tasso medio di profitto energetico. La struttura della regola media dipende dal modo in cui l'informazione viene accumulata mentre l'animale passa da un fiore ai successivi durante un giro di foraggiamento. Per ciascun fiore, in una sequenza di n visite, siano Ri la ricompensa per il fiore iesimo e Ti il tempo richiesto per ottenere la ricompensa. Il modello Harder-Real assume che le api massimizzino il guadagno energetico netto atteso da calcoli che si basano su attributi del singolo fiore, ossia la media della serie di Ri/Ti,
formula. [4]
Tale schema di calcolo della media permette di ottenere il valore aspettato del rapporto tra le due variabili casuali E(R/T) che porta alla massimizzazione del guadagno di energia a breve termine. Tuttavia, molti autori hanno osservato che gli organismi dovrebbero massimizzare il guadagno a lungo termine piuttosto che quello a breve termine.
Massimizzare i guadagni a lungo termine equivale a calcolare il rapporto dei valori di aspettazione delle variabili casuali, ossia E(R)/E(T). In effetti vi è un intervallo di possibilità tra guadagno completamente a breve termine e guadagno completamente a lungo termine che corrisponde a differenti modi di elaborare le informazioni provenienti da una successione di visite a fiori. Per esempio, ricompense e lassi di tempo potrebbero essere cumulati tramite coppie successive di fiori nella successione, ossia
formula [5 ]
o attraverso triplette di fiori (E3), quadruplette di fiori (E4) e così via. Nel limite teorico in cui n → ∞ l'equazione [5] è uguale a E∞ =E(R)/E(T) che corrisponde al tasso medio di guadagno energetico a lungo termine.
Abbiamo calcolato il tasso medio di guadagno netto di energia Ek come una funzione dell'insieme k su cui i campioni sono cumulati per ciascuna distribuzione di ricompense flore ali utilizzata nei nostri esperimenti del 1980; abbiamo inoltre usato le espressioni con base fisiologica per R e T dal modello Harder-Real (v. figura 4). La dimensione dell'insieme determina la struttura fine dell'elaborazione di una particolare sequenza di informazioni. In tutti i nostri esperimenti, la correlazione tra il tasso medio di guadagno energetico e la preferenza osservata è stata più alta per l'ottimizzazione a breve termine (ossia per una dimensione dell'insieme pari a k = 1 o k = 2) e più bassa per l'ottimizzazione a lungo termine (Real, 1992). Questi risultati suggeriscono chiaramente che i bombi formano regole funzionali che sono basate sui tassi di profitto ottenuti da singoli fiori oppure, al massimo, da coppie di fiori; di conseguenza ciò comporta una massimizzazione del guadagno energetico a breve termine.
Codificazione delle regole funzionali
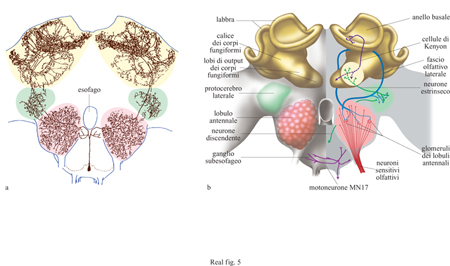
Pochi anni fa M. Hammer e R. Menzel, dell'Università statale di Berlino, studiando le api domestiche scoprirono una base neuronale incredibilmente semplice per l'apprendimento di una ricompensa, la quale potrebbe costituire la chiave per comprendere la codificazione del comportamento di scelta floreale. Successivamente, i due studiosi hanno identificato un neurone specifico, VUMmx1, nel ganglio sottoesofageo dell'ape (fig. 5) che trasmette informazioni sulla ricompensa in esperimenti di condizionamento classico (Hammer, 1993).
In molti esperimenti tradizionali di apprendimento che utilizzano le api domestiche, gli individui possono apprendere ad associare una ricompensa (acqua zuccherata) a odori specifici. Il condizionamento avviene quando l'acqua zuccherata, posta direttamente sulle antenne dell'ape, viene accoppiata all'emanazione di uno specifico odore. La stimolazione antennale data dalla ricompensa provoca un riflesso che fa estendere la proboscide dell'ape; in seguito al condizionamento, la somministrazione dell'odore in assenza degli stimoli-ricompensa fa estendere ugualmente la proboscide. Hammer scoprì che la stimolazione diretta del neurone VUMmxl può sostituire la stimolazione antennale utilizzando ricompense zuccherine e che la stimolazione di VUMmxl accoppiata a odori porta allo stesso tipo di risposta condizionata che si osserva nell'apprendimento associato a ricompensa. I risultati di Hammer evidenziano il substrato neuronale coinvolto nell'apprendimento per associazione a ricompensa ne II 'ape domestica. Hammer e Menzel hanno anche dimostrato che la stimolazione di VUMmxl può essere sostituita da una somministrazione diretta di octopammina (il presunto neurotrasmettitore) nelle regioni del cervello dell'ape che corrispondono ai lobi antennali e ai sensilli basiconici.
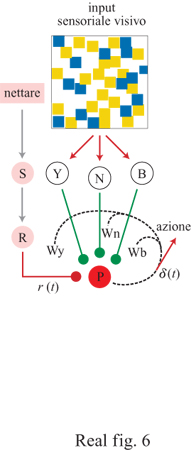
P.R. Montague e collaboratori (1995) hanno costruito una rete neurale semplice, basata su VUMmxl, che include le caratteristiche essenziali del comportamento di scelta floreale in condizioni di incertezza e che mima i risultati dei nostri esperimenti di scelta, effettuati utilizzando bombi in campi artificiali caratterizzati da tipi di colorazioni floreali che differivano nella distribuzione delle ricompense. Nella simulazione l'individuo in cerca di cibo si muove in un'arena tridimensionale. Sul piano dell'arena vi è un campo diviso in quadrati gialli e blu che rappresentano fiori di due tipi. Da una data postazione nell'arena, l'ape può vedere una porzione del campo determinata da un cono di visione che cambia non appena l'ape si muove. L'architettura della rete neurale è raffigurata nella figura (fig. 6). Questa unità accoppia lo stimolo ricompensa r(t) a ingressi colorati e l'uscita da P modifica il comportamento motorio verso i fiori di un certo tipo o verso la ricerca casuale in un nuovo campo di visione. L'associazione tra lo stimolo dato dal colore e la ricompensa segue una regola di apprendimento hebbiana (v. anche il saggio di L. Maffei e N. Berardi, nel terzo volume) che nella simulazione diviene l'equivalente della regola Rescorla-Wagner del condizionamento classico (Rescorla e Wagner, 1972). La velocità di apprendimento è caratterizzata da un parametro λ e con 0 < λ < 1 tale che quando λ è elevato, l'ape impara molto rapidamente e modifica il comportamento a breve termine in seguito a esperienze immediate. Un basso valore di λ corrisponde a una mancanza di risposta a breve termine, ma mantiene la capacità di rispondere a modificazioni medie a lungo termine dell'ambiente.
Il legame tra i nostri esperimenti, che descrivono una regola funzionale per il singolo bombo, e la rete neurale di Montagne viene stabilito tramite la forma specifica dello stimolo ricompensa r(t) come una funzione del volume di nettare dei fiori incontrati nell'arena. Nella rete neurale le ricompense sono misurate in valori in accordo con la derivata funzione biomeccanica (v. figura 4); Montague e collaboratori utilizzano questa relazione come output del neurone ricompensa R. Il modello del comportamento di foraggiamento dei bombi è stato costruito da Montague e collaboratori in un'arena artificiale in cui il campo di fiori simulato seguiva le distribuzioni di nettare nei fiori gialli e blu utilizzati nei miei esperimenti originali (Real, 1981), ossia fiori blu contenenti 2 μI di nettare ciascuno e fiori gialli contenenti per un terzo 6 μI e 0 μI per i restanti due terzi. La simulazione all'elaboratore produsse un risultato in notevole accordo con i pattem osservati nella scelta fatta dai bombi (v. figura 3), ma solo quando la velocità di apprendimento λ nella rete neurale era elevata (λ = 0,9). Così, la rete neurale corrispondeva alla prestazione delle api quando l'architettura della regola di apprendimento corrispondeva a un'estrema reattività a breve termine. Queste simulazioni di reti neurali, basate su meccanismi neuronali molto plausibili, sostengono ulteriormente l'affermazione generale che le api utilizzano solo le esperienze immediate a breve termine e le regole funzionali basate su visite al singolo fiore per formulare le loro decisioni alimentari.
l meccanismi neuronali coinvolti nel comportamento decisionale delle api potrebbero essere una curiosità biologica rilevante per lo studio del comportamento umano. Montague e collaboratori hanno ipotizzato in modo convincente che il sistema nervoso dell'ape potrebbe costituire un modello ideale per studiare l'organizzazione generale del sistema nervoso nell'affrontare scelte complesse. Il sistema neuromodulatore mediato dal neurotrasmettitore octopammina, che nell'ape è diffusamente ramificato, ha il suo analogo nei sistemi neuronali ramificati, modulati dalla dopammina, che ascendono la corteccia cerebrale dei mammiferi. Di conseguenza, potremmo trovarci nella posizione unica di analizzare le basi neuronali delle decisioni complesse effettuate dagli esseri umani utilizzando questo semplice modello di invertebrato.
Regole per la cooperazione
In natura vi sono innumerevoli esempi di organismi che si comportano in modo cooperativo o altruistico: se spaventato, un cervo dalla coda bianca agita la coda segnalando ai cervi vicini la presenza di un potenziale pericolo; un castoro sbatterà la coda come segnale di pericolo; diverse specie di uccelli, da giovani, ritardano l'epoca della riproduzione per rimanere nel nido ad aiutare i propri genitori nell'allevamento dei fratelli (v. anche il saggio di G. Wilkinson, Cooperazione). Tuttavia, il comportamento cooperativo sia negli esseri umani sia negli animali è stato considerato piuttosto anomalo da un punto di vista evolutivo. La cooperazione implica alcune forme di aiuto del prossimo, spesso con costi per l'individuo che la intraprende. Tuttavia, da un punto di vista evolutivo gli organismi dovrebbero agire sempre per favorire i propri interessi individuali piuttosto che gli interessi di altri organismi. Infatti, Darwin osservò che il successo evolutivo può migliorare non solo riproducendosi di più, ma anche facendo in modo che altri si riproducano meno. Così, da un punto di vista biologico danneggiare altri individui piuttosto che aiutarli può persino essere vantaggioso poiché riduce il loro successo riproduttivo. Come si origina allora il comportamento cooperativo?
Le condizioni che promuovono la cooperazione tra individui che interagiscono tra loro sono state spesso studiate utilizzando il gioco del dilemma del prigioniero (PDG, Prisoner's Dilemma Game). In questo gioco vi sono due individui che giocano l'uno contro l'altro. Ciascun giocatore ha due scelte (può cooperare o defezionare), agisce indipendentemente dall'altro e non sa come l'altro giocherà nella mano successiva del gioco, ma può ricordare come ha giocato nelle mani precedenti. Beneficio o danno per ciascun giocatore dipendono dalla combinazione delle scelte fatte da entrambi (v. anche il saggio di G. Wilkinson, Cooperazione). l possibili risultati per ciascun giocatore sono illustrati nella tabella (tab. I).
Se entrambi i giocatori decidono di cooperare, ciascuno riceve una ricompensa pari a 3 punti. Il premio potrebbe consistere in denaro per gli esseri umani o, per esempio, semi per una cavia. La mutua cooperazione è una buona strategia, poiché entrambe le parti ottengono una buona ricompensa. Se un giocatore coopera ma l'altro defeziona, quest 'ultimo ottiene una grande ricompensa, pari a 5 punti, mentre quello che coopera non ottiene nulla. Se entrambi i giocatori decidono di defezionare, ciascuno ottiene l punto. Come si dovrebbe procedere in questo gioco? Supponiamo di essere il giocatore 1 e di ritenere che il giocatore 2 coopererà. Se anche noi cooperassimo, otterremmo 3 punti. Tuttavia, se defezionassimo otterremmo 5 punti. Che succederebbe se ritenessimo che il giocatore 2 defezioni? In questo caso, cooperando otterremmo O punti mentre defezionando otterremmo l punto. Di conseguenza, se l'avversario sceglie di cooperare, è meglio defezionare, e se l'avversario sceglie di defezionare, è meglio defezionare. In tal modo, indipendentemente da ciò che fa l'avversario, è meglio scegliere di defezionare anche se per entrambi sarebbe meglio cooperare. È qui il dilemma. Un comportamento individualistico porta a risultati che sono di minor beneficio per entrambi i giocatori rispetto a quanto avverrebbe se si fossero messi d' accordo per cooperare. Vi sono condizioni in cui il comportamento cooperativo può essere favorito rispetto al comportamento interamente individualista?
In un'analisi brillante e creativa di questo problema R. Axelrod (1984), dell'Università del Michigan, invitò i più famosi teorici della teoria dei giochi a suggerire strategie (regole funzionali) per vincere il gioco del dilemma del prigioniero quando la partita potesse essere svolta ripetutamente contro lo stesso giocatore, il cosiddetto PDG iterato. Quale fu la regola che vinse sulle altre? Axelrod ricevette strategie da 63 diversi teorici, le cui regole variavano in complessità dalle più semplici ad altre basate su computazioni e aggiustamenti complicati di probabilità, condizionate dal comportamento nelle sessioni precedenti. Sorprendentemente, tuttavia, emerse una regola come chiara strategia dominante, la regola nota come TFT (Tit For Tat, occhio per occhio). Questa regola si è rivelata non soltanto la migliore strategia utilizzata contro altre strategie, ma anche la più semplice tra quelle esaminate. Funziona in tal modo: nella prima scelta il giocatore che applica la regola TFT sceglie sempre di cooperare, poi sceglie la mossa dell'avversario, qualunque essa sia nell'ultima mano. Se l'avversario defeziona, applicando la regola TFT, il giocatore defeziona; se coopera, continua a cooperare. Questa regola si rivelò migliore delle altre quando tutte le regole furono giocate una contro l'altra. Il successo di TFT come regola funzionale si basa su tre caratteristiche. In primo luogo, si comincia con il cooperare e perciò si beneficia di altre strategie cooperative nella popolazione. In secondo luogo, tuttavia, ci si vendica immediatamente passando a defezionare confrontandosi con un giocatore che decide di non cooperare. Tuttavia, si è immediatamente pronti a tornare a cooperare se un avversario torna a cooperare.
Questa semplice strategia sembra imbattibile se ben stabilita in una popolazione di giocatori. Tuttavia, proviamo a immaginare una popolazione di giocatori che scelgono solo di defezionare. Come potrebbe la regola TFT imporsi su questa popolazione? Alla prima mano il giocatore TFT perderebbe da tutti, mentre nelle successive non farebbe di meglio che defezionare. Così, in questa popolazione, la strategia TFT sarebbe perdente. Come si potrebbe diffondere? Axelrod collaborò con un noto biologo evoluzionista, W.D. Hamilton, per risolvere questo problema. Essi notarono che se piccoli gruppi di giocatori formassero associazioni, la strategia TFT sarebbe frn dall'inizio in vantaggio contro altre strategie. Hamilton e Axelrod dimostrarono quindi che TFT richiede solo gruppi molto piccoli di giocatori per ottenere un vantaggio iniziale e diffondersi nella popolazione.
Conclusioni
Le migliori regole funzionali associate ai tre problemi di comportamento discussi in questo saggio (scegliere un partner, scegliere risorse, decidere se cooperare) racchiudono alcune caratteristiche comuni dell'organizzazione comportamentale. Ciascuna regola funzionale dominante è semplice e dunque in grado di essere codificata in semplici strutture neuronali. Inoltre, ciascuna regola funzionale dominante sembra capace di vedere solo da vicino. In altre parole, la migliore strategia è guardare solo al passato prossimo o alle condizioni attuali dell'ambiente piuttosto che incorporare informazioni in funzione di lunghi lassi di tempo. Per le api che raccolgono il nettare, ciò che importa è il tasso di energia che ottengono dal singolo fiore. Per i cooperatori, l'unico evento che forma il comportamento è la risposta immediatamente precedente degli avversari. Ritengo che questa 'miopia' nel decidere abbia qualche vantaggio evolutivo generale (Real, 1992). Perché? Gli organismi vivono in ambienti molto strutturati nel tempo e nello spazio. Il verificarsi di specifici fenomeni non è in genere un evento casuale: infatti tali fenomeni mostrano alcune forme di correlazione sia nel tempo sia nello spazio. La grandezza della ricompensa all'interno dei fiori è in genere correlata spazialmente, così che fiori che offrono grandi ricompense sono in prossimità di fiori che offrono grandi ricompense mentre fiori che danno piccole ricompense sono in prossimità di fiori che danno piccole ricompense. Gruppi di individui geneticamente correlati sono spesso associati l'uno all'altro nello spazio e nel tempo e potrebbero formare i nuclei necessari per la diffusione delle strategie cooperative. Spesso incontri di alto valore (ricompense in cibo o forse partner) sono correlati temporalmente. In questi casi la 'miopia' potrebbe essere un valore, poiché permetterebbe all'organismo di tracciare le variazioni nel suo ambiente e modificare le decisioni basate su conseguenze e condizioni del futuro prossimo. È questa struttura fondamentalmente semplice delle regole funzionali 'miopi' che permette la necessaria flessibilità per rispondere a condizioni ambientali che variano rapidamente.
Bibliografia citata
AXELROD, R.M. (1984) The evolution of cooperation. New York, Basic Books.
BATESON, M., KACELNIK, A. (1996) Rate currencies and the foraging starling: the fallacy of the averages revisited. Behav. Ecol., 7, 341-352.
GALLISTEL, C.R. (1990) The organization of learning. Cambridge, Mass., MIT Press.
HAMMER, M. (1993) An identified neuron mediates the unconditioned stimulus in associative olfactory leaming in honey bees. Nature, 366, 59-63.
HARDER, L., REAL, L.A. (1987) Why are bumblebees risk-averse. Ecology, 68, 1104-1108.
JANETOS, A.C. (1980) Strategies of female choice: a theoretical analysis. Behav. Ecol. Sociobiol., 7, 107-112.
MONTAGUE, P.R., DAYAN, P., PERSON, C., SEJNOWKI, T.J. (1995) Bee foraging in uncertain envirouments using predictive hebbian leaming. Nature, 377, 725-728.
REAL, L.A. (1981) Uncertainty and pollinator-plant interactions: the foraging behavior bees and wasps on artificial flowers. Ecology, 62, 20-26.
REAL, L.A. (1990) Search theory and mate choice. I. Models of single-sex discrimination. Am. Nat., 136, 376-404.
REAL, L.A. (1992) Information processing and the evolution of cognitive architecture. Am. Nat., 140, S108-S145.
REBOREDA, J.C., KACELNIK, A. (1991) Risk sensitivity in starlings: variability in food amount and food delay. Behav. Ecol., 2, 301-308.
RESCORLA, R.A., WAGNER, A.R. (1972) A theory of Pavlovian conditioning: variations of the effectiveness of reinforcement and non-reinforcement. In Classical conditioning, voI. 2, a c. di Black A.H., Prokasy W.F., Appleton-Century-Crofts Publishers, pp. 64-99.
Bibliografia generale
KREBS, J.R., DAVIES, N.B. Behavioural ecology: an evolutionary approach. Oxford, Blackwell Publishers, 1991.
REAL, L.A. Behavioral mechanisms in evolutionary ecology. Chicago, University of Chicago Press, 1994.